4. 4. Диференційованість функції в точці

Означення 3.2. Функція називається диференційованою в точці , якщо приріст функції в цій точці можна записати в вигляді:

, де – число.

Теорема 3.1. Для того, щоб функція була диференційованою в точці необхідно і достатньо щоб вона в цій точці мала скінченну похідну .

Теорема 3.2. Якщо функція диференційована в деякій точці, то вона і неперервна в цій точці.

Дана теорема не є достатньою: зворотне твердження невірно, функція може бути неперервною і не мати похідної.

Рис. 3.3.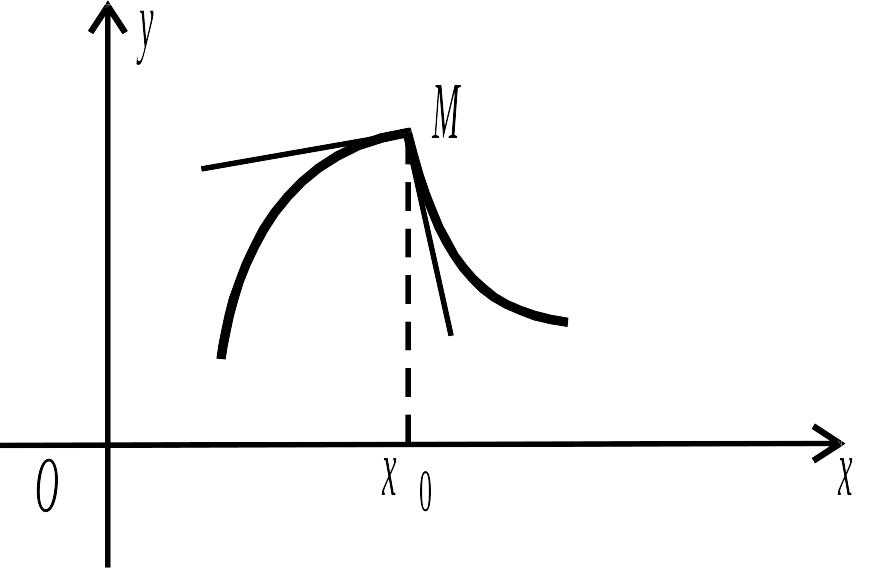

На рис. 3.3 зображено графічно функцію, неперервну в точці M, але вона не має єдиної дотичної у цій точці, тобто єдиної границі . Тому говорять, що в такому випадку функція не має похідної в точці .

Аналогічно поняттю односторонньої границі, вводять поняття односторонньої похідної. Лівостороння і правостороння похідні в точці визначаються, відповідно, як односторонні границі:

і .

Якщо в точці існує похідна, то її односторонні похідні в цій точці існують і рівні між собою. І навпаки: якщо існують і рівні односторонні похідні функції, то існує і похідна в точці.

Рис. 3.4.

Прикладом неперервної функції, що не має похідної в точці є функція (рис. 3.4).

Ця функція неперервна при , але не є диференційованою, і функція не має єдиної дотичної. Обчислимо односторонні похідні функції в точці ; при цьому врахуємо, що

Маємо: , .

Як бачимо , що підтверджує відсутність похідної функції в точці .

Надалі, стверджуючи, що функція має похідну в точці , будемо розуміти, що вона скінченна.

5. 5. Похідні елементарних функцій

1. Похідна сталої функції дорівнює нулю: якщо , то .

Для даної функції , , а значить і .

2. Якщо , то .

Для даної функції , , , .

3. Доведемо, що . Маємо:

.

4. , .

Для першого випадку ,

.

Аналогічно можна одержати похідну функції .

5. Розглянемо функцію і доведемо, що .

Маємо: . Тоді одержимо похідну:

.

6. 6. Основні правила диференціювання

Нехай функції і мають похідні в точці .

1. Похідна алгебраїчної суми функцій дорівнює алгебраїчній сумі похідних функцій, тобто

. (3.4)

Нехай . Дамо приріст , тоді функції і одержують прирости, відповідно рівні і , а функція одержить приріст . Нове значення функції буде , функції – і отже

,

, .

Остаточно одержимо .

2. Похідна добутку. Доведемо, що

. (3.5)

Нехай . Дамо приріст , тоді функції і одержують прирости, рівні і , їхні нові значення , . При цьому і

.

Застосовуючи теореми про границю суми і добутку, будемо мати: .

Врахуємо, що , , . Виходить , що і було потрібно довести.

Зокрема, якщо

,

тобто сталий множник можна виносити за знак похідної.

Використовуючи останню формулу і похідну натурального логарифма, можна одержати похідну функції . Враховуючи, що , одержимо

. (3.6)

3. Похідна частки. Розглянемо функцію . Припустимо, що функція відмінна від нуля в розглянутій точці . Доведемо, що

. (3.7)

Дійсно, приріст функції, що відповідає приросту аргументу дорівнює

, .

Застосовуючи теорему про границі частки і добутку і, враховуючи неперервність функції в точці , одержимо, що

.

Приклад 3.5. Довести, що , .

Розв’язання. Маємо:

.

Аналогічно виводиться формула похідної функції .