Необхідна і достатня умова випуклості (увігнутості) графіка функції.

Якщо в усіх точках деякого проміжку друга похідна функції від'ємна, то графік функції на цьому проміжку випуклий; якщо друга похідна додатня, то графік функції на цьому проміжку увігнутий.

Рис. 3.16.

Доведення проведемо для випадку, коли на проміжку . Теорема буде доведена, якщо встановимо, що всі точки графіка функції на розглянутому проміжку лежать нижче дотичної, проведеної в деякій точці цього проміжку (рис. 3.16).

Рівняння кривої має вигляд . Нехай – ордината змінної точки дотичної. Рівняння дотичної до графіка функції в точці має вигляд .

Оцінимо різницю ординат точок кривої і дотичної для одного й того ж : .

Застосувавши до різниці теорему Лагранжа, одержимо , де точка лежить між точками і .Винесемо за дужки загальний множник і до виразу в дужках знову застосуємо теорему Лагранжа, одержимо

,

де точка лежить між і . Якщо то , , за умовою , звідки випливає, що або , тобто графік функції розташований під дотичною. Якщо , то , , за умовою , звідси випливає, що або , тобто графік розташований під дотичною.

Аналогічно можна довести теорему для випадку, якщо друга похідна функції на проміжку додатня.

Очевидно, що в точці перегину дотична, якщо вона існує, перетинає криву, оскільки з одного боку від цієї точки крива лежить під дотичною, а з іншого боку – над нею (рис. 3.17, а, б)

Рис. 3.17.

Необхідна умова точки перегину.

Якщо точка є точкою перегину графіка функції, то функція в точці визначена, а друга похідна дорівнює нулю або не існує.

Необхідна умова просто ілюструється графічно на рис. 3.17, а, б, але не є достатньою. Наприклад, для функції друга похідна при , але в цій точці графік не має перегину, оскільки крива увігнута на всій числовій вісі.

Достатні умови точки перегину.

Якщо функція визначена в точці , двічі диференційована в околі точки і при переході через точку друга похідна змінює знак, то точка є точкою перегину.

Дійсно, якщо при і при , то ліворуч точки з абсцисою графік функції є випуклим, а праворуч точки – увігнутим. Отже, точка є точкою перегину графіка функції. Аналогічно описується випадок, коли при і при .

Очевидно, що в точці друга похідна функції дорівнює нулю (рис. 3.17, а) або не існує (рис. 3.17, б).

Можна запропонувати такий алгоритм знаходження проміжків випуклості, увігнутості і точок перегину графіка функції.

1. Знайти область визначення функції.

2. Знайти першу і другу похідні функції.

3. Знайти точки, в яких друга похідна функції дорівнює нулю або не існує.

4. Область визначення знайденими точками розбити на проміжки і дослідити знак другої похідної на кожному з проміжків.

Якщо на проміжку , то це проміжок увігнутості, якщо , то це проміжок випуклості. Точки перегину при цьому розділяють проміжки випуклості й увігнутості.

Зауважимо, що можна при дослідженні розглядати похідні вищих порядків.

Приклад 3.22. Знайти проміжки випуклості, увігнутості і точки перегину графіка функції (крива Гауса).

Розв’язання. Відзначимо, що функція визначена на всій числовій прямій. Для неї , . Друга похідна обертається в нуль, якщо , звідки , . Зміна знака другої похідної показана на рис. 3.18.

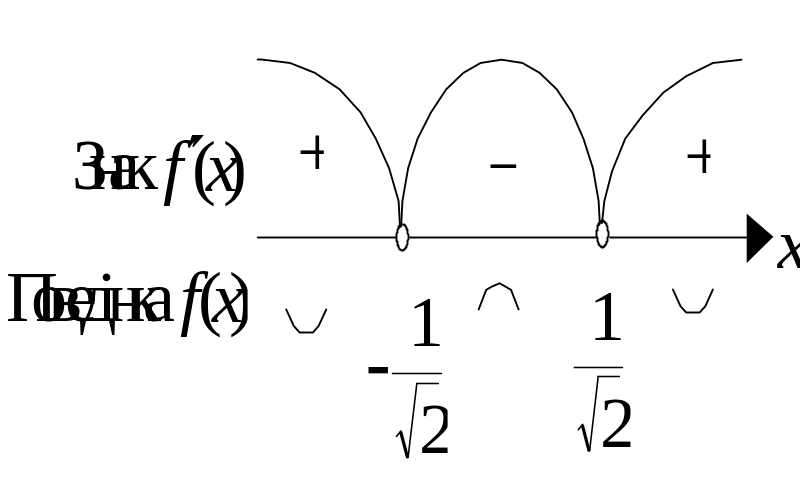
Рис. 3.18.

Очевидно, що точки з абсцисами і є точками перегину графіка функції. При цьому