ImplicitPlot[{u[X,y]0,V[X,y]0},{X,-8,8},{y,-8,8},PlotStyleThickness[0.01]]

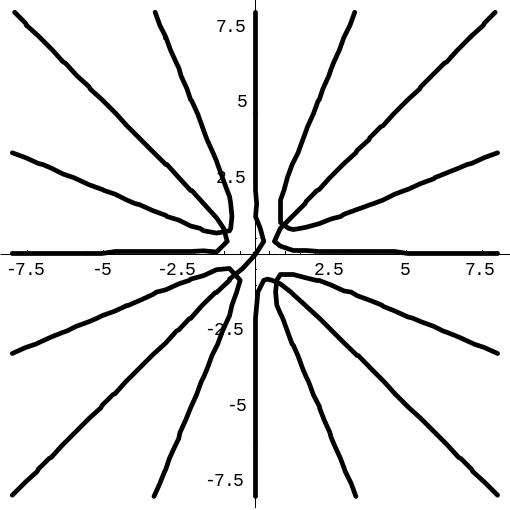
Находим вещественные и мнимые части корней многочлена.

FindRoot[{u[x,y]0,v[x,y]0},{x,2.5},{y,2.5}]

{x0.919211999,y0.945348721}

FindRoot[{u[x,y]0,v[x,y]0},{x,-2.5},{y,2.5}]

{x-0.952558813,y0.718413163}

FindRoot[{u[x,y]0,v[x,y]0},{x,-2.5},{y,-2.5}]

{x-0.584868552,y-0.598690581}

FindRoot[{u[x,y]0,v[x,y]0},{x,2.5},{y,-2.5}]

{x0.618215376,y-0.865071303}

Пусть многочлен степени с действительными коэффициентами. Запишем его в следующем виде

(3.4.1)

Матрица

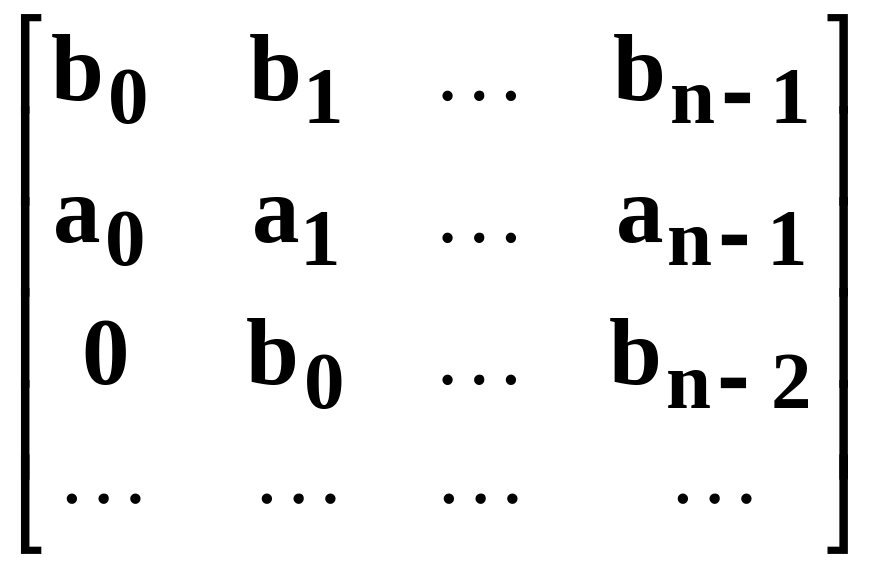(3.4.2)

называется матрицей Гурвица многочлена (3.4.1). Те элементы , которые в многочлене (3.4.1) отсутствуют, в матрице Гурвица этого многочлена полагаются равными нулю. Миноры этой матрицы порядков 1,2,…,n, стоящие в левом верхнем углу, называются определителями Гурвица.

Справедлив следующий результат: для того, чтобы все корни многочлена с действительными коэффициентами и положительным старшим коэффициентом лежали в левой полуплоскости необходимо и достаточно, чтобы все определители Гурвица, составленные для этого многочлена, были положительны. Этот результат носит название критерия Гурвица.

Система Mathematica позволяет легко проверить, выполняется ли для заданного многочлена критерий Гурвица или нет.

Пример 3.4.6. Проверить выполнение критерия Гурвица для следующего многочлена чётной степени

Решение.

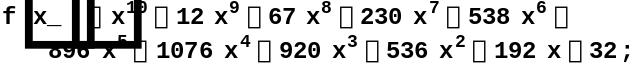
Строим массив из коэффициентов данного многочлена

L=CoefficientList[f[x],x];

Находим число элементов в массиве и определяем чётность этого числа

n=Length[L]

11

L=Reverse[L];

Строим для данного многочлена матрицу Гурвица.

n1=(n-1)/2;

A=Table[0,{n,1,2*n1}];

B=Table[0,{n,1,2*n1}];

Do[A[[n]]=L[[2*n-1]],{n,1,n1+1}]

Do[B[[n]]=L[[2*n]],{n,1,n1}]

H={{0},{0}};G=Table[0,{n,1,n1}];

<<LinearAlgebra`MatrixManipulation`

G[[1]]={B,A};

Do[G1=G[[1]];Do[G1=TakeColumns[AppendRows[H,G1],2*n1],{m,1,k-1}];G[[k]]=G1,{k,2,n1}]

GG=G[[1]];

Do[GG=AppendColumns[GG,G[[k]]],{k,2,n1}]

Проверяем выполнение критерия Гурвица.

Table[Det[SubMatrix[GG,{1,1},{m,m}]]>0,{m,2*n1}]

{True,True,True,True,True,True,True,True,True,True}

Следовательно, все корни многочлена лежат в левой полуплоскости

Пример 3.4.7. Проверить выполнение критерия Гурвица для следующего многочлена нечётной степени

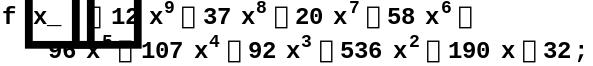
Строим массив из коэффициентов данного многочлена.

L=CoefficientList[f[x],x];

Находим число элементов в массиве и определяем чётность этого числа.

n=Length[L]

10

L=Reverse[L];

Строим для данного многочлена матрицу Гурвица.

n1=(n-2)/2;

A=Table[0,{n,1,2*n1+1}];

B=Table[0,{n,1,2*n1+1}];

Do[A[[n]]=L[[2*n-1]],{n,1,n1+1}]

Do[B[[n]]=L[[2*n]],{n,1,n1+1}]

H={{0},{0}};G=Table[0,{n,1,n1}];

<<LinearAlgebra`MatrixManipulation`

G[[1]]={B,A};

Do[G1=G[[1]];Do[G1=TakeColumns[AppendRows[H,G1],2*n1+1],{m,1,k-1}];G[[k]]=G1,{k,2,n1}]

GG=G[[1]];

Do[GG=AppendColumns[GG,G[[k]]],{k,2,n1}]

H=Table[0,{m,1,n1}];

B1=Table[0,{n,1,2*n1+1}];

Do[B1[[n]]=Join[H,B][[n]],{n,1,2*n1+1}]

GG1=Table[0,{n,1,2*n1+1}];

Do[GG1[[n]]=GG[[n]],{n,1,2*n1}]

GG1[[2*n1+1]]=B1;

T=Table[Det[SubMatrix[GG1,{1,1},{n,n}]]>0,{n,1,2*n1+1}]

{True,True,False,False,False,True,True,True,True}

Из полученного результата следует, что не все корни рассматриваемого многочлена расположены в левой полуплоскости.

Предположим, что коэффициенты многочлена заданы в виде рациональной функции параметра. В этом случае система Mathematica позволяет найти область значений параметра, в которой корни рассматриваемого многочлена будут лежать в левой полуплоскости ( иначе говоря, рассматриваемый многочлен будет устойчивым).

Пример 3.4.8. Для многочлена

найти область устойчивости.

Решение.

0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

L=CoefficientList[f[x],x];

n=Length[L]

5

L=Reverse[L];

n1=(n-1)/2;

A=Table[0,{n,1,2*n1}];

B=Table[0,{n,1,2*n1}];

Do[A[[n]]=L[[2*n-1]],{n,1,n1+1}]

Do[B[[n]]=L[[2*n]],{n,1,n1}]

H={{0},{0}};G=Table[0,{n,1,n1}];

<<LinearAlgebra`MatrixManipulation`

G[[1]]={B,A};

Do[G1=G[[1]];Do[G1=TakeColumns[AppendRows[H,G1],2*n1],

{m,1,k-1}];G[[k]]=G1,{k,2,n1}]

GG=G[[1]];

Do[GG=AppendColumns[GG,G[[k]]],{k,2,n1}]

T=Table[Det[SubMatrix[GG,{1,1},{m,m}]],{m,2*n1}];

R=T[[1]]>0;Do[R=R&&T[[n]]>0,{n,2,4}]

N[Reduce[R,a]]

a>1.98271

0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000Предположим теперь, что коэффициенты многочлена зависят от двух параметров. Рассмотрим следующий

Пример 3.4.9. Найти область устойчивости многочлена

.

Решение.

L=CoefficientList[f[x],x];

n=Length[L]

5

L=Reverse[L];

n1=(n-1)/2;

A=Table[0,{n,1,2*n1}];

B=Table[0,{n,1,2*n1}];

Do[A[[n]]=L[[2*n-1]],{n,1,n1+1}]

Do[B[[n]]=L[[2*n]],{n,1,n1}]

H={{0},{0}};G=Table[0,{n,1,n1}];

<<LinearAlgebra`MatrixManipulation`

G[[1]]={B,A};

Do[G1=G[[1]];Do[G1=TakeColumns[AppendRows[H,G1],2*n1],

{m,1,k-1}];G[[k]]=G1,{k,2,n1}]

GG=G[[1]];

Do[GG=AppendColumns[GG,G[[k]]],{k,2,n1}]

T=Table[Det[SubMatrix[GG,{1,1},{m,m}]],{m,2*n1}];

R=T[[1]]>0;Do[R=R&&T[[n]]>0,{n,2,4}]

<<Graphics`InequalityGraphics`