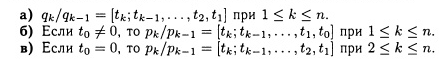7.5. Подходящие дроби
Вполне очевидно, что [t0,t1,t2, …, tk], для каждого к представляет собой действительное число. Запишем первые четыре подходящие дроби и упростим их, выразив каждую как отношение двух действительных чисел, где как числитель, так и знаменатель выражены через ti. Особый интерес будут представлять числитель и знаменатель каждой из подходящих дробей.
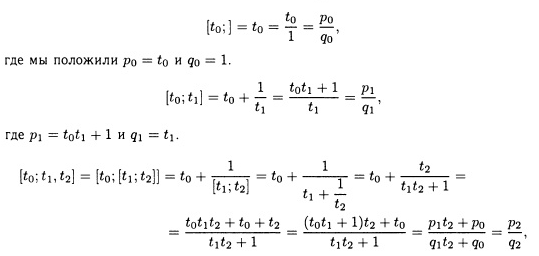
где р2 = p1t1 + p0 и q2 = q1t2 + q0 Подобным образом вычисляем
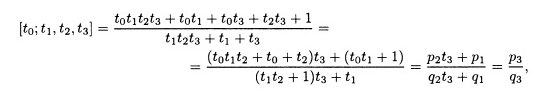
где р3 = p2t3 + p1 и q3 = q2t3 + q1 в каждом случае число [t0,t1,t2,…,tk] “переформировывается" из представления цепной дробью без какого-либо "сокращения" и образует отношение двух полиномов Р и Q в переменных t0,t1,t2, …, tk , т.е.
![]() Справедливым
является и то, что q0,q1,q2
и q3
положительны, поскольку получены
путем умножения и сложения положительных
чисел. Рассмотренные примеры дают
основание сформулировать следующую
теорему.
Справедливым
является и то, что q0,q1,q2
и q3
положительны, поскольку получены
путем умножения и сложения положительных
чисел. Рассмотренные примеры дают
основание сформулировать следующую
теорему.
ТЕОРЕМА 7.11. Пусть n — неотрицательное целое число и t0,t1,t2,…,tn] — конечная цепная дробь, которая рекурсивно определяет конечные последовательности p0 ,p1 … pn и q0 ,q1 … qn следующим образом:

ДОКАЗАТЕЛЬСТВО. Не представляет труда методом математической индукции показать, что qk > 0 при 0 ≤ k ≤ n. Эту часть теоремы предоставляем доказать читателю. Выше было показано, что теорема справедлива при к = 0,1 и 2, т.е. [t0] = p0 /q0 [t0,t1] = p1 /q1, [t0,t1,t2] = p2 /q2 Предположим, что 2 ≤ k < n, и для любой цепной дроби [b0,b1,b2, …, bk] и любого j 0 ≤ j ≤ k справедливо утверждение о том, что [b0,b1,b2, …, bj] = рj'/qj'. где рj' и qj' определены способом, аналогичным (а)-(с), но для цепной дроби [b0,b1,b2, …, bm] Тогда
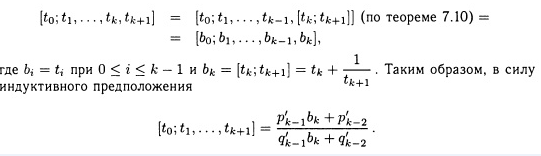

Поскольку bi = ti при 0 ≤ i ≤ к - 1, имеем, что для таких i pi = рi' и qi = q'i. Подставляя соответствующие выражения для bk, рi' и qi’, получаем
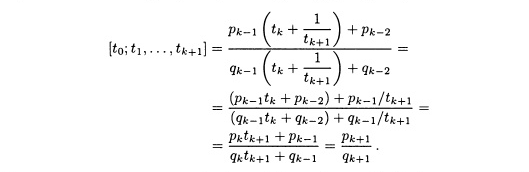
Следовательно, по индукции, [t0,t1,t2,…,tk]= pk/qk при 0 ≤ k ≤ n.
Числа pk и qk (теорема 7.11) определены вне зависимости от того, что они могут быть использованы как числитель и знаменатель выражения, равного k-ой подходящей дроби. Рекурсивное отношение, заданное теоремой 7.11, обеспечивает быстрый способ вычисления подходящих дробей для заданной цепной дроби, поскольку числитель р, и знаменатель pi можно вычислить одновременно и достаточно просто. Например, для х = [-4; 2,5,2,1] =[t0,t1,t2,t3,t4] подходящие дроби можно вычислить согласно приведенной ниже таблице:
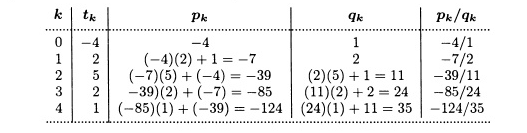
Так что х = -124/35, т.е. числу, породившему цепную дробь [—4; 2,5,2,1] (см. раздел 5.1).
Благодаря рекурсивному способу задания цепных дробей, имеется значительное количество соотношений, связывающих подходящие дроби через числители и знаменатели, рk и qk, введенные теоремой 7.11. Чтобы запись этих соотношений сделать справедливой при k = 0, зачастую удобно определять рk и qk при k = -1, положив
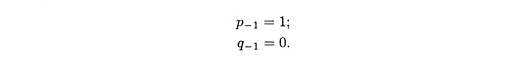
Таким образом, р1 = p0t1 +p-1 = t0t1 + 1 и q1 = qot1 + q-1 = 1• t1 +0 = t1, как в теореме 7.11.
ТЕОРЕМА 7.12. Если t0,t1,t2,…,tn] - конечная цепная дробь, где ti — действительные числа, pk и qk— заданы теоремой 7.11, тогда
![]()

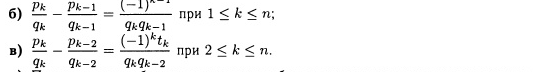
г) Подходящие дроби четного порядка образуют возрастающую последовательность, т.е.
![]()
а подходящие дроби нечетного порядка образуют убывающую последовательность, т.е.
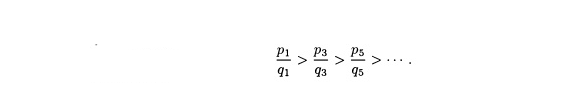
при 0 ≤ j ≤ [n/2] и 0 ≤ i ≤ [(n - 1)/2], где слева равенство имеет место, когда n четное, а справа равенство имеет место, когда п нечетное.
д) Если дробь [t0;t1,…,tn] — простая, то qk ≥ k при 0 ≤ k ≤ n.
е) Если дробь [t0;t1,…,tn] — простая, то qk < qk+1 при 1 ≤ k ≤ n-1 и q0 ≤ q1
ДОКАЗАТЕЛЬСТВО, а) При k = 1 p1q0 – p0q1 = (t1t0 + 1)(1) - t0t1 = 1 = (-1)1-1 по теореме 7.11. Пусть 2 ≤ m < n и допустим, что формула в части (а) справедлива при k = m. Показано, что формула имеет место при k = т + 1. Опять, используя теорему 7.11, имеем
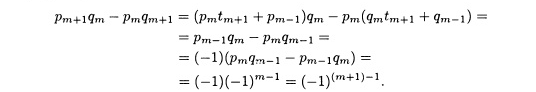
Таким образом, формула в части (а) имеет место при 1 ≤ k ≤ п. Также p0q-1 – qop-1 =t0•0- 1•1 = -1 и формула справедлива при k = 0.
б) Утверждение теоремы следует из части (а), если в соответствующем равенстве при k ≥ 1 произвести деление на qkqk-1 .
в) Если k ≥ 2, то по теореме 7.11
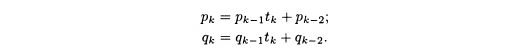
Умножение первого из равенств на qk-2, а второго — на pk-2 дает
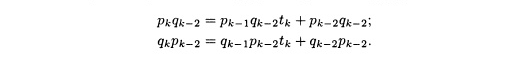
Вычитая второе равенство из первого, получаем
![]()

Теперь, учитывая утверждение в части (а), получаем
![]()
Разделив на qkqk-2 > 0, получаем желаемый результат:
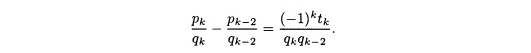
г) Если 2 ≤ k ≤ n и k— четное, то k — 2 тоже четное и k — 2 ≥ 0. Поэтому (-1)k = 1 и из утверждения в части (в) вытекает, что
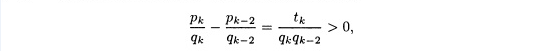 поскольку
tk
и
qkqk-2
положительные
при к
≥
1. Если 3≤
k<n
н k
—
нечетное, то k
-
2 также нечетное и k
- 2 ≥ 1. В этом случае (-l)k
=
-1, так что из утверждения в части (в)
вытекает, что
поскольку
tk
и
qkqk-2
положительные
при к
≥
1. Если 3≤
k<n
н k
—
нечетное, то k
-
2 также нечетное и k
- 2 ≥ 1. В этом случае (-l)k
=
-1, так что из утверждения в части (в)
вытекает, что

так как tк и qkqk-2положительны при к ≥ 3.
Если
n
нечетное, то согласно (б)
![]() так что [t0,t1,t2,
…,
tn]
=
так что [t0,t1,t2,
…,
tn]
=
Pn/qn
больше, чем наибольшая подходящая дробь
четного порядка, Pn-1/qn-1
Если п
четное, то
![]() так что [t0,t1,t2,
…,
tn]
= Pn/qn
меньше, чем Pn-1/qn-1
наименьшая подходящая дробь нечетного
порядка, Pn-1/qn-1
так что [t0,t1,t2,
…,
tn]
= Pn/qn
меньше, чем Pn-1/qn-1
наименьшая подходящая дробь нечетного
порядка, Pn-1/qn-1
Доказательство пунктов (д) и (е) оставляем за читателем.
Подходящие дроби для х = [-4; 2,5,2,1] вычислены ранее в данном разделе и приведены в таблице. Подводя итог этим результатам в контексте части (г), находим, что
![]() Непосредственным
вычислением определяем также, что
Непосредственным
вычислением определяем также, что
![]() Значение
теоремы 7.12 состоит в том, что она точно
устанавливает, что последовательные и
взаимно исключающие подходящие дроби
могут отличаться не более, чем на
величину, обратно пропорциональную
“знаменателям" подходящих дробей,
а также, что подходящие дроби альтернативно
больше, чем [t0,t1,t2,
…,
tn].
И меньше, чем [t0,t1,t2,
…,
tn]
Значение
теоремы 7.12 состоит в том, что она точно
устанавливает, что последовательные и
взаимно исключающие подходящие дроби
могут отличаться не более, чем на
величину, обратно пропорциональную
“знаменателям" подходящих дробей,
а также, что подходящие дроби альтернативно
больше, чем [t0,t1,t2,
…,
tn].
И меньше, чем [t0,t1,t2,
…,
tn]
Практический интерес представляют некоторые отношения Pn/qn числителей и знаменателей подходящих дробей. Эти отношения приведены в следующей теореме, доказательство которой предоставляется читателю.

ТЕОРЕМА 7.13. Для конечной цепной дроби t0,t1,t2, …, tn]