7.4. Цепные дроби

В данной главе алгоритм деления и алгоритм Евклида будут применяться доста­точно часто. Рассмотрим сначала рациональные числа а/b, где а и b — целые числа и 6 > 0. Если алгоритм деления применен к целым числам а и b, где b > 0, то существуют единственные целые числа t (частное) и r (остаток) такие, что

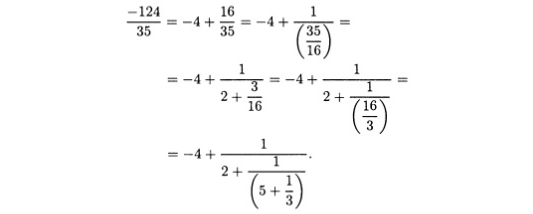
Для а = -124 и 6 = 35 имеем

Переписав последние два равенства и перейдя к рациональным числам, получаем

Воспользовавшись функцией целой части числа, отношения можем переписать в таком виде

при этом дробный остаток r/b обладает свойством 0 ≤ r/b < 1. Если r ≠ 0, равенства можно переписать следующим образом:

где b/r > 1. Алгоритм деления можно применить снова и получить b = rt' + r' и 35 = (16)(2) + 3. Таким образом, обращая дробный остаток и применяя алгоритм деления снова и снова, указанным способом получаем выражение рационального числа -124/35:

Поскольку дробь 1/3 имеет числителем 1, нельзя далее сокращать 3/1, используя алгоритм деления. Выражение

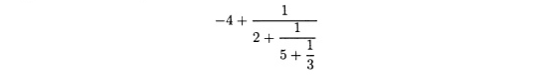
называется цепной дробью и представляет собой альтернативный способ запи­си рационального числа -124/35. В связи с тем, что цепная дробь имеет ре­гулярную структуру и числители всегда равны 1, для точного задания цепной дроби необходимо упомянуть только числа -4, 2, 5 и 3, поэтому записыва­ем -124/35 = (-4; 2,5,3). Числа -4, 2, 5 и 3 называются элементами цеп­ной дроби или неполными частными, поскольку порождены алгоритмом деле­ния. Точка с запятой отмечают особую природу первого члена -4. Например, [3; 7] = 3 4- 1/7 = 22/7, но

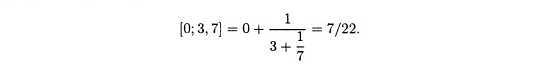Возвращаясь к цепной дроби -124/35 = [-4;2,5,3], замечаем, что

3 = (3 — 1) 4-1 = (3 — 1) 4-1/1. Таким образом, можно записать

так что запись -124/35 = [—4;2,5,2,1] тоже имеет место, однако в ней на послед­нем шаге алгоритм деления не использован. Пример подсказывает, что каждое рациональное число имеет два различных представления в виде цепной дроби с целыми числами в качестве элементов: в одном представлении последний элемент больше 1, а в другом — равен 1.

Если х — действительное, но не рациональное число, алгоритм деления не применим; однако, используя функцию целой части, можно получить представ­ление х в виде цепной дроби длины п способом, аналогичным рациональному случаю. Таким образом, для действительного, но не рационального числа х име­ется единственное число t₀. где t₀ ≤ х < t₀ + 1 такое, что t₀ = [x]. Тогда

есть так называемая дробная часть х. Если х₁ = 1/у₁, тогда

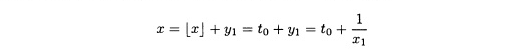
и х₁ > 1. Пусть t₁ = [x₁], y₂ = x₁ - [x₁] и х₂ = 1/у₂, т.к. у₂ > 0. Тогда

x₁ = t₁ – 1/x₂, где х₂ > 0. Сочетание этих равенств дает

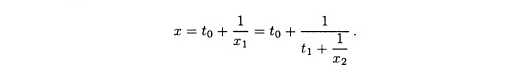
Продолжая в том же духе, получаем

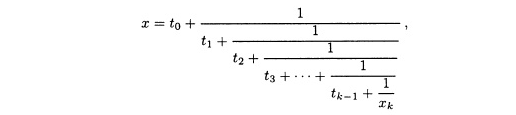
где t_i — целое число для каждого i , t_i > 0 для i ≥ 1, х_k — иррациональное действительное число и х_k > 1. Можно также записать

Например, пусть х = = 1.7320508-. Построим представление числа х в виде цепной дроби следующим образом:

где

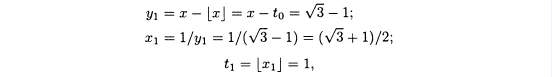
Где

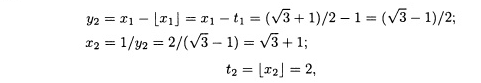
Где

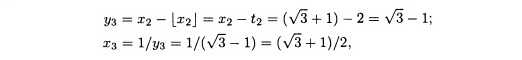
таким образом,

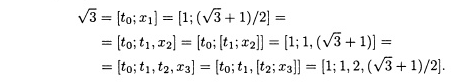
Но поскольку x₃ = x₁, структура повторяется , поэтому

и т.д.

О тсюда выводим следующее рекурсивное определение цепной дроби.

ОПРЕДЕЛЕНИЕ 7.9. Для конечной последовательности t₀,t₁,t₂, …, t_n дей­ствительных чисел, где n ≥ 0 и t_i > 0 для i ≥ 1, определим конечную цепную дробь [t₀,t₁,t₂, …, t_n] следующим образом:

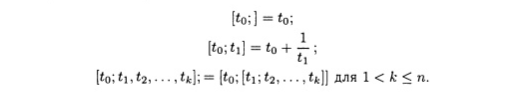
Числа t₀,t₁,t₂, …, t_n называются неполными частными, или элементами цеп­ной дроби. Цепная дробь [t₀,t₁,t₂, …, t_n] называется простой, если t, — це­лое число для каждого i, т.е. каждый элемент цепной дроби есть целое число. Числа [t₀], [t₀,t₁], [t₀,t₁,t₂]…[t₀,t₁,t₂, …, t_k]…[t₀,t₁,t₂, …, t_n] называ­ются подходящими дробями цепной дроби [t₀,t₁,t₂, …, t_n]. [t₀,t₁,t₂, …, t_k], где есть k-я подходящая дробь при 0 ≤ k ≤ n. Для удобства обозначения запись [t₀,t₁,t₂, …, t_k], использованная при к = 0. будет означать [t₀]. Бу­дем говорить, что две цепные дроби [t₀,t₁,t₂, …, t_n] и [b₀,b₁,b₂, …, b_m] равны почленно, если n = m и t = b_i при 0 ≤ i ≤ n. Если х — действительное число и X = [t₀,t₁,t₂, …, t_n], тогда будем говорить, что [t₀,t₁,t₂, …, t_n] есть представление цепной дробью числа х. Два представления называются сов­падающими, или равными, если они равны почленно.

Следующая теорема дает иной способ разложения цепной дроби на подхо­дящие дроби.

ТЕОРЕМА7.10. Если n — положительное целое число и [t₀,t₁,t₂, …, t_n] — цепная дробь, тогда для каждого к, 1 ≤ k ≤ n,

ДОКАЗАТЕЛЬСТВО. Равенство докажем методом математической индукции. Ес­ли п = 1, по определению, [t₀,t₁] = [t₀,[t₁]]- Предположим, что утверждение теоремы выполняется при n = m, т.е. для любой цепной

для 1 ≤ j ≤ m. Рассмотрим n = m + 1. Пусть [t₀,t₁,t₂, …, t_m+1] — цепная дробь и 1 < k < m + 1. Тогда

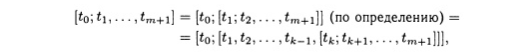
полагая по индуктивному предположению b_i = t_i+1 и j = k - 1. Таким образом,

согласно определению цепной дроби. Следовательно, по методу индукции теорема справедлива.