8.7.19. Дадим наглядную интерпретацию теоремы раздела 8.7.16, когда т.Е. Когда система уравнений с неизвестными имеет вид:
См. рис. 8.23а, который поясняется так.
Открытый шар радиуса
с центром в точке
это
трёхмерная
окрестность
точки
Трёхмерная
окрестность
с центром в точке
с концами
на оси
это
(одномерная)
окрестность
точки
участок
двумерного множества нулевого уровня
функции
который расположен в пересечении
окрестности
с горизонтальным слоем
т.е.
геометрический
образ уравнения
при
принадлежащих пересечению
окрестности
с горизонтальным слоем
Аналогично,
геометрический
образ уравнения
при
принадлежащих пересечению
окрестности
с горизонтальным слоем
Одномерная линия
есть
пересечении двух двумерных поверхностей
и
Естественно, линия
есть
геометрический образ множества решений
системы уравнений
при принадлежащих пересечению окрестности с горизонтальным слоем
проекция
линии
на координатную плоскость
проекция
линии
на координатную плоскость
это
график неявной функции
график
неявной функции
Эти функции
и
есть результат локальной однозначной
разрешимости системы уравнений
относительно переменных
и
при фиксированной переменной
такими, что
принадлежат пересечению
окрестности
с горизонтальным слоем
Теорема 8.7.16 утверждает, что линия
есть также пересечение двух двумерных
цилиндрических поверхностей (они на
рисунке 8.23а не показаны). Одна из этих
цилиндрических поверхностей имеет в
качестве направляющей линию
а в качестве образующих прямые,
параллельные координатной плоскости
другая из этих цилиндрических поверхностей
имеет в качестве направляющей линию
а в качестве образующих прямые,
параллельные координатной плоскости
Касательное (одномерное) линейное
многообразие
(см. рис. 8.23а) к линии
в точке
есть пересечение двух двумерных
касательных плоскостей (на рис. 8.23а эти
плоскости не показаны) к двумерным
поверхностям
и
в точке
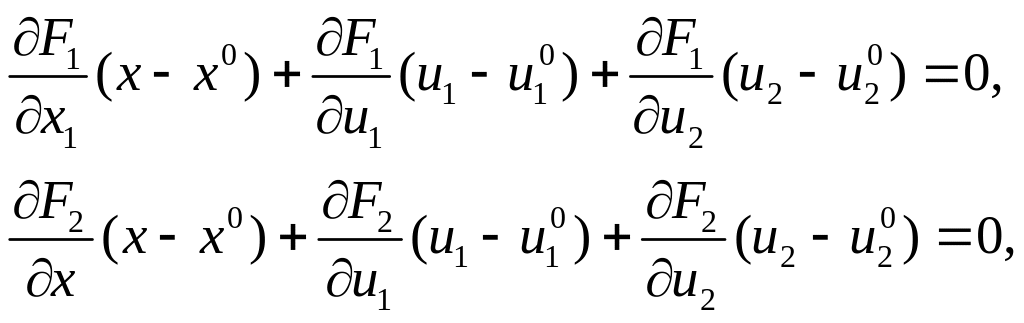
где
Система двух
линейных уравнений с тремя
переменными
имеет вид:
Каждому их этих уравнений соответствует двумерная плоскость в трёхмерном пространстве.
В связи с тем, что
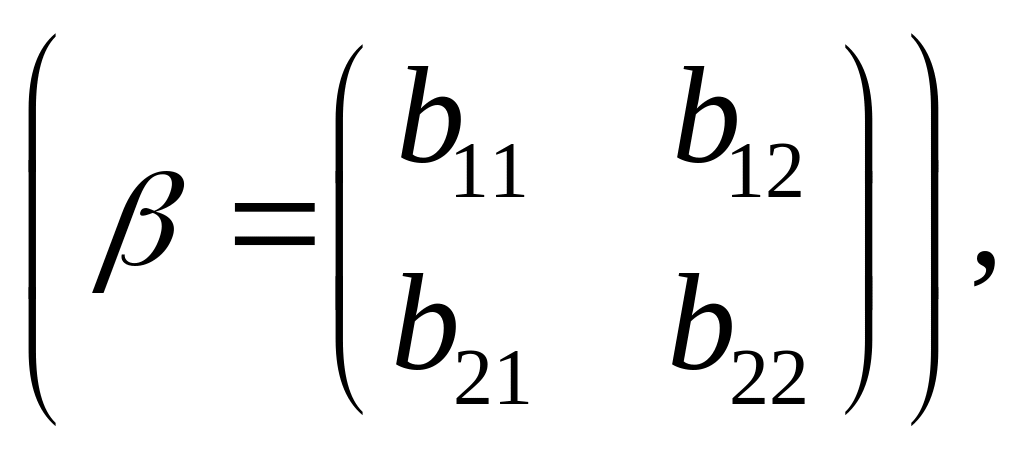
эти плоскости пересекаются по прямой которая представляет собой линейное многообразие решений системы двух линейных уравнений с тремя переменными, эта система эквивалентна следующей:
(ибо
откуда вытекает, что всё линейное
многообразие решений однозначно
проектируется на координатную ось
(см. рис. 8.23б).
На рис. 8.23б плоскость, изображающая уравнение
плоскость, изображающая уравнение
Плоскости
и
пересекаются по прямой
линейному
многообразию решений системы двух
линейных уравнений с тремя переменными
Прямая
проекция
прямой
на координатную плоскость
уравнение прямой
Аналогично
проекция
прямой
на координатную плоскость
уравнение прямой
На рисунке 8.23б чётко видно, что вся
прямая
однозначно проектируется на координатную
плоскость
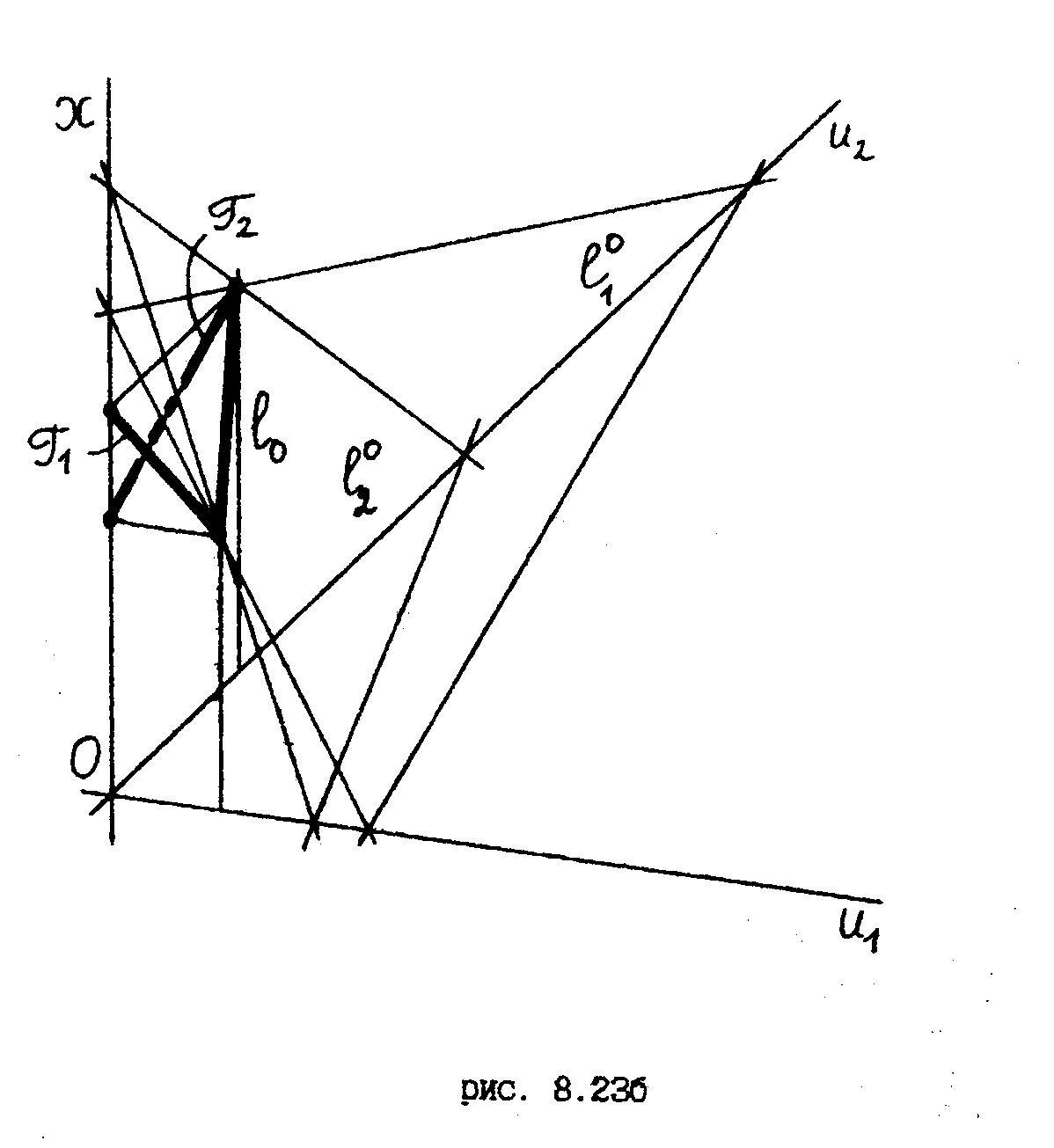
Отметим, что на рис. 8.23б и на рис. 8.23а одни и те же буквы обозначают как глобальные линейные объекты (рис. 8.23б), так и их локальные нелинейные аналоги (на рис. 8.23а).
8.7.20 Примеры.
1) Найдём первый дифференциал и частные
производные неявной функции
задаваемой уравнением
(Здесь
Затем выпишем уравнение двумерной
касательной плоскости к двумерному
множеству
в точке
Если функцию
подставив в уравнение
то это уравнение превратится в тождество
по
и
Дифференциал от этого тождества равен
нулю, дифференциал также обладает
инвариантностью формы. Таким образом,
имеем (считая, что
откуда
Следовательно,
Если использовать формулы раздела
8.7.13 (в этом примере
то получим для (первых) частных производных
и
те же самые формулы:
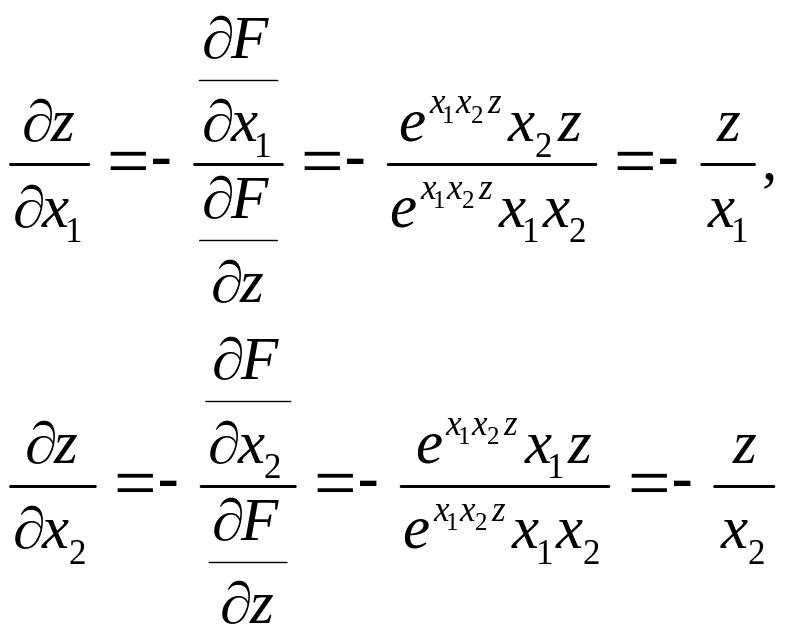
и
Уравнение касательной плоскости в точке
к множеству нулевого уровня
имеет вид:
или
Для
имеем:
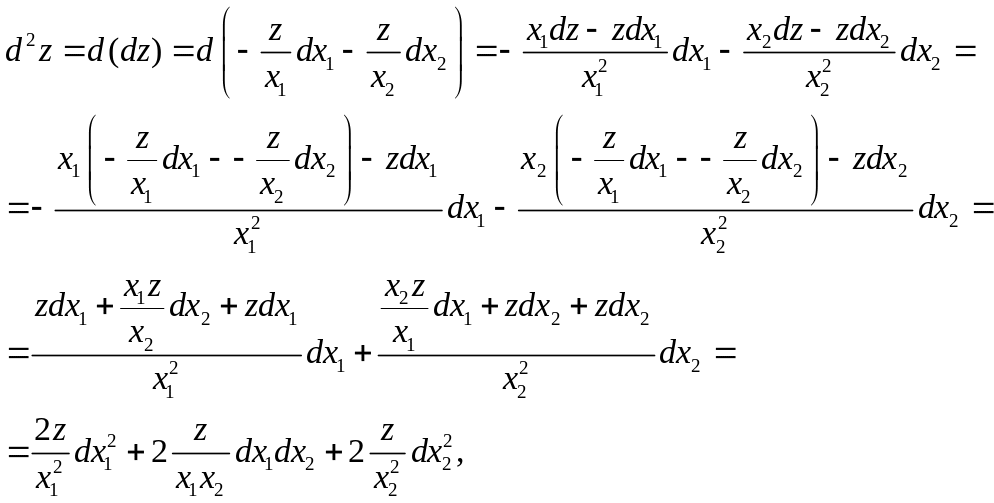
Найдём
непосредственно:
Аналогично получаются выражения
Имея явный вид вторых частных производных
можно выписать явное выражение для
которое, естественно, совпадает с
выписанным выше.
2) Найдём первый дифференциал и частные
производные системы неявных функций
задаваемых системой уравнений:
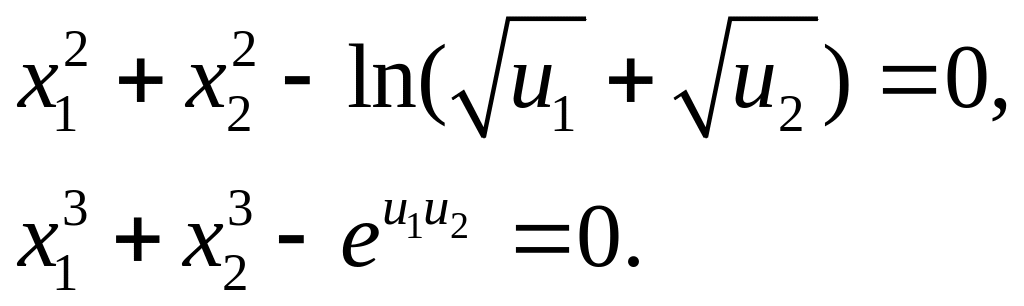
Здесь множество
является двумерным. Выпишем так же
уравнения касательного линейного
многообразия к двумерному множеству
в точке
Неявные функции
подставим в уравнение системы и получим
тождества по
и
Дифференциалы от этих тождеств равны
нулю, дифференциалы обладают инвариантностью
формы. Таким образом, имеем (считая, что
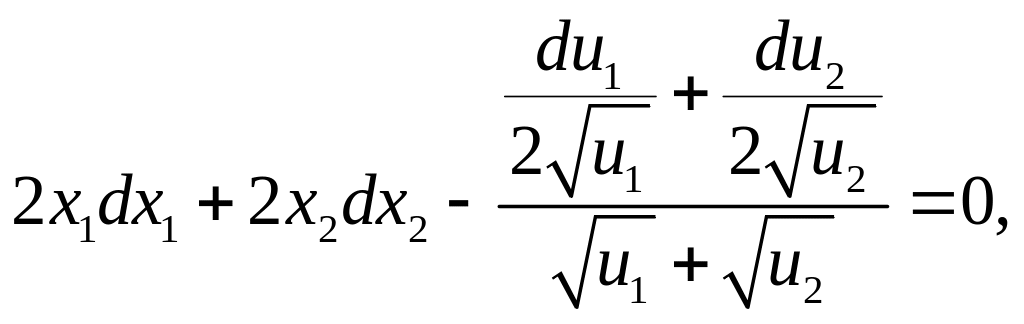
Перепишем полученную систему относительно
переменных
и
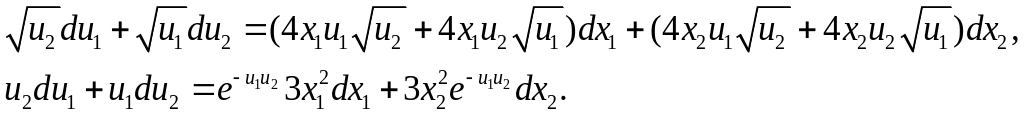
Умножим первое уравнение на
потом из него вычтем второе уравнение,
разделим обе части полученного уравнения
на
и получим
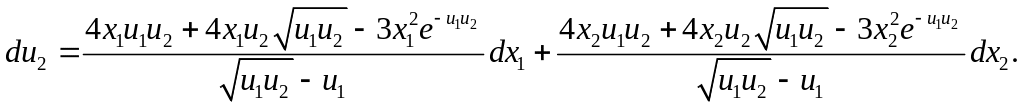
Поскольку
в оба уравнения входя симметрично, имеем
(по аналогии):
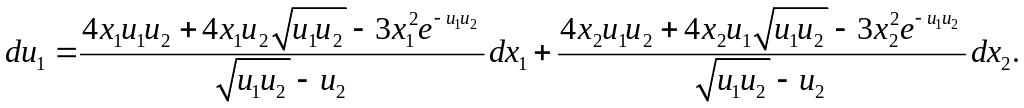
Имея первые дифференциалы (неявных)
функций
и
можем выписать в качестве (первых)
частных производных этих функций по
переменным
и
коэффициенты дифференциалов
и
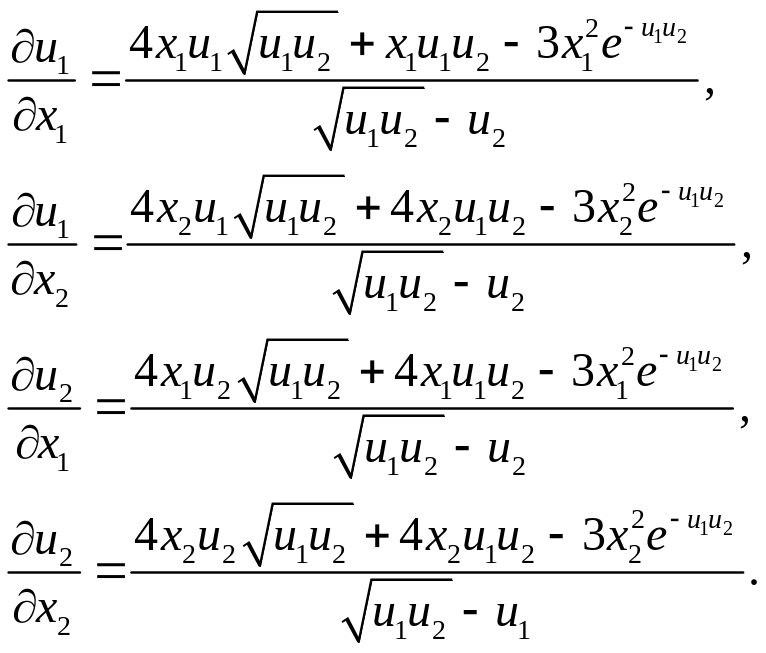
Уравнения двумерного касательного
многообразия к двумерному множеству
в точке
имеют вид:
Упражнения.
1. Найти производную по переменной
неявной функции
определяемой уравнением
а)
б)
в)
г)
д)
2. Найти производную неявной функции
определяемой уравнением
в точке
написать уравнение касательной
к графику функции
построить касательную
на плоскости
3. Найти дифференциал
и (первые) частные производные по
переменным
и
неявной функции
определяемой уравнением
а)
б)
в)
4. Найти дифференциал
неявной функции
определяемой уравнением
частные производные этой функции по
переменным
и
написать уравнение касательной плоскости
к графику
функции
в точке
построить в пространстве
эту плоскость
5. Найти дифференциал
и
и производные по переменной
системы неявных функций
определяемых системой уравнений:
а)
б)
в)
6. Найти дифференциалы и системы неявных функций определяемых системой уравнений:
производные этих неявных функций.
Написать уравнения касательных двумерных
плоскостей к множествам нулевого уровня
функций
и
в точке
Написать уравнение одномерного
касательного линейного многообразия
к множеству
в точке
7. Найти дифференциалы
и
и (первые) частные производные по
переменным
и
системы неявных функций
определяемых системой уравнений:
а)
б)
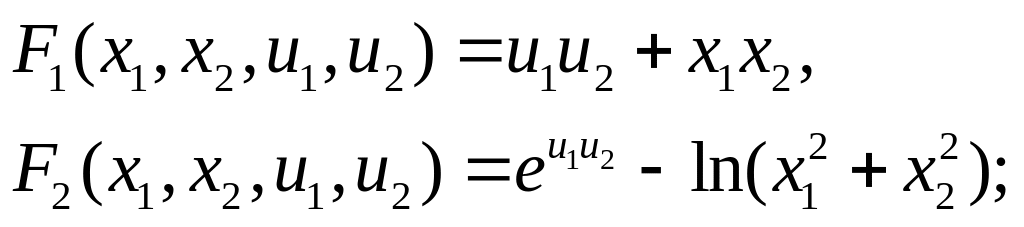
в)
8. Найти дифференциалы и (первые) частные производные по переменным и системы неявных функций определяемых системой уравнений:
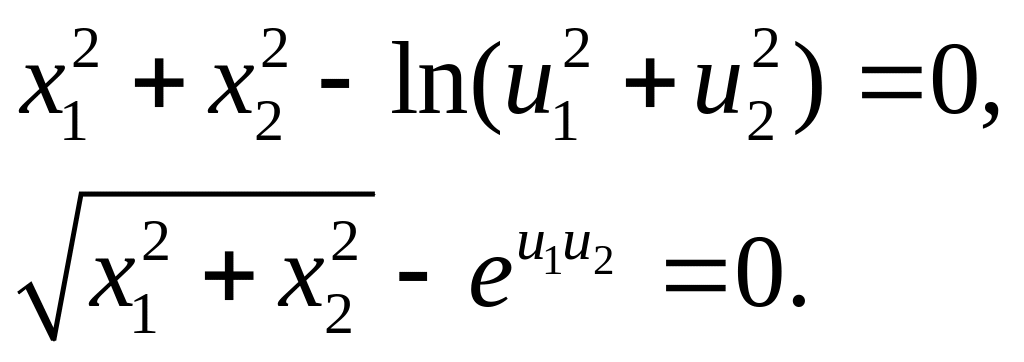
Написать уравнения касательных трёхмерных плоскостей к множествам нулевого уровня функций:
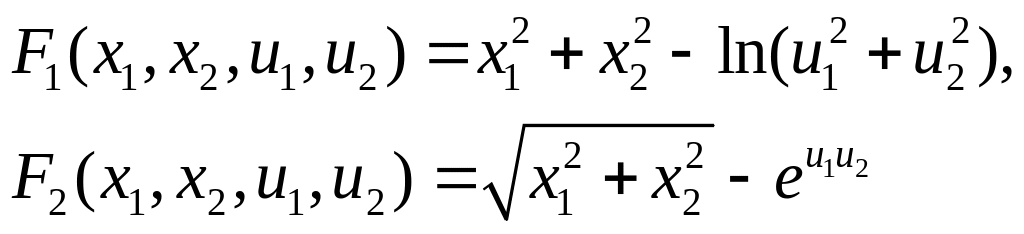
в точке Написать уравнение двумерного касательного линейного многообразия к множеству описываемому системой уравнений
в точке
9. Найти первую и вторую производные по переменной неявной функции определяемой уравнением
а)
б)
в)
10. Найти все первые и вторые производные по переменным и неявной функции определяемой уравнением
а)
б)
11. Найти первый и второй дифференциалы неявной функции определяемой уравнением
а)
б)
12. Найти первый и второй дифференциалы системы неявных функций и определяемых системой уравнений:
13. Найти первый и второй дифференциалы системы неявных функций и определяемых системой уравнений:
а)
б)
