Элементы теории неявных функций – учебное пособие .

8.7.1 Определение

Неявной называется функция одной переменной если она задана уравнением ещё не разрешены относительно (см. раздел 1.6.1).

Неявной называется функция двух переменных и если она задана уравнением ещё не разрешённым относительно

Ниже приведены общие определения неявной функции нескольких переменных задаваемой уравнением и набора неявных функций задаваемых системой уравнений

Область математического анализа, в которой анализируются вопросы существования, единственности, непрерывности и дифференцируемости неявных функций, называется теорией неявных функций. Элементы этой теории составляют содержание нижеследующих разделов.

8.7.2 Пример.

Решение уравнения относительно переменной при фиксированной переменной существует (например, такое решение: Однако это решение не является единственным. Можно рассмотреть ещё несколько вариантов выражения переменной через переменную

если если

если если (рис. 8.11).

Ч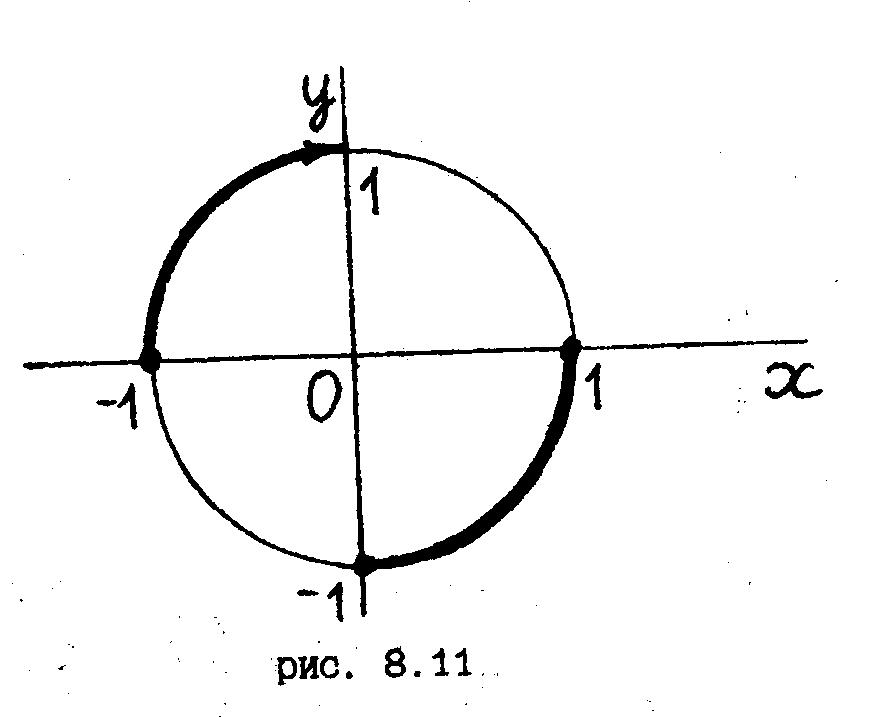 исло вариантов можно неограниченно расширять за счёт, например, последовательного деления отрезков и т.д. Приведём ещё один пример варианта разрешения уравнения относительно переменной

если

если

если

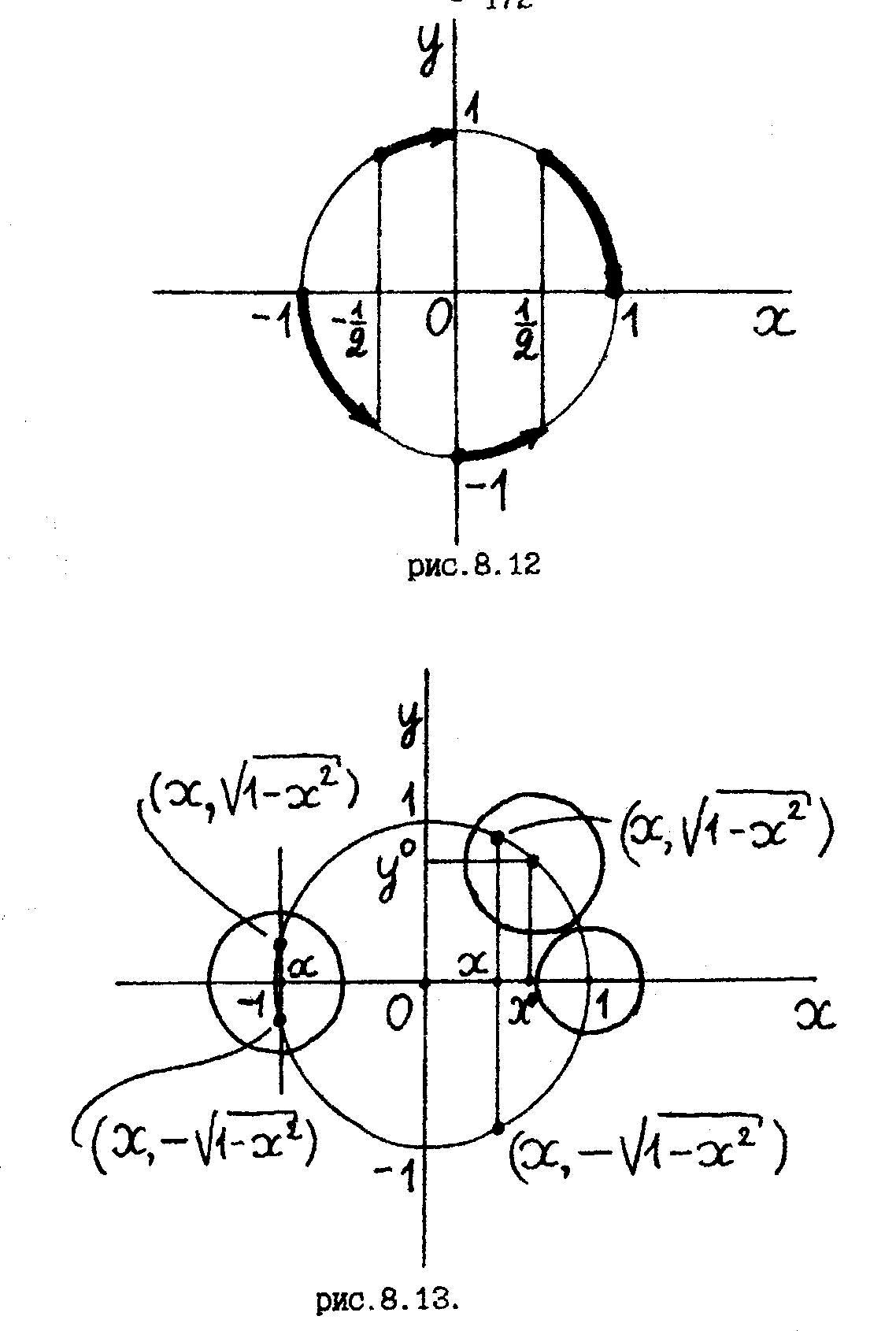
если (рис. 8.12).

8.7.3 Пример раздела 8.7.2 показывает, что даже в случае простого выражения уравнение в целом разрешимо относительно переменной при фиксированной переменной но не единственным образом. Поэтому задачу о разрешимости уравнения относительно переменной при фиксированной переменной следует уточнить, поставив вопрос об однозначной локальной разрешимости уравнения относительно переменной при фиксированной переменной

Вернёмся к примеру раздела 8.7.2. Если рассматривать только точки удовлетворяющие уравнению и близкие к точке (рис. 8.13), то для любого фиксированного и близкого к существует единственное решение уравнения т.е. это уравнение однозначно локально разрешимо относительно переменной при фиксированной переменной

Отметим, что точка близка к точке (рис. 8.13), а точка не является близкой к точке и поэтому не рассматривается. Если же рассматривать точки удовлетворяющие уравнению и близкие к точке (или к точке (см. рис. 8.13), то для любого фиксированного и близкого к (или близкого к 1) существует два решения уравнения т.е. это уравнение вблизи точки (или точки уже не является однозначно локально разрешимым относительно переменной при фиксированной переменной

Рассмотрим геометрическую интерпретацию описанной аналитической ситуации. На рис. 8.13 хорошо видно, что если близка к то вертикальная прямая, проходящая через точку протыкает участок окружности, расположенный около точки только один раз (в точке т.е. участок окружности, расположенный около точки однозначно проектируется на ось Если близка к (или к 1), то вертикальная прямая, проходящая через точку протыкает участок окружности, расположенный около точки (или около точки обязательно в двух точках (в точке и в точке т.е. участок окружности, расположенный около точки (или точки однозначно не проектируется на ось ибо точка на оси есть проекция двух точек участка, а не одной точки участка, как это было в случае точек, близких к точке Отметим, что участок окружности, расположенный около точки (или точки однозначно проектируется на ось

Приведённый простой пример иллюстрирует тот факт, что задача об однозначной локальной разрешимости уравнения относительно переменной при фиксированной переменной эквивалентна задаче об однозначном локальном проектировании на ось участка линии нулевого уровня функции

Первая теорема о неявной функции даёт достаточное условие однозначной локальной разрешимости уравнения относительно переменной при фиксированной переменной (т.е. достаточное условие о локальном существовании и единственности неявной функции и, следовательно, достаточное условие однозначного локального проектирования на ось участка нулевой линии уровня функции Очевидно, этот локальный участок нулевой линии уровня и есть график функции

Далее вместо символов и будут использованы символы и чтобы подчеркнуть равноправие обеих переменных.

8.7.4 Теорема (теорема 1 о неявной функции)

Пусть функция

1. дифференцируема в

2. 

3. 

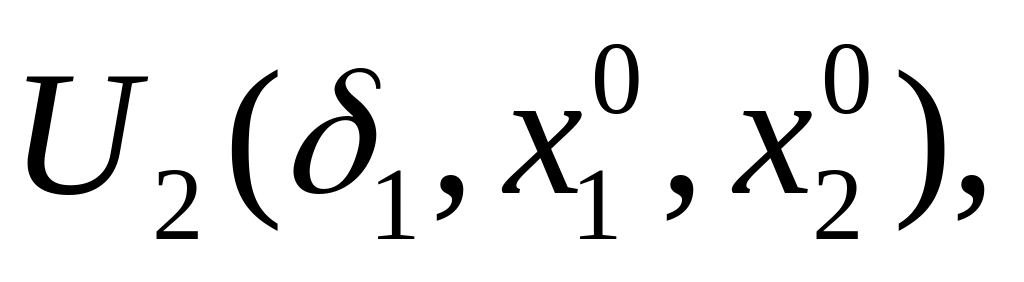
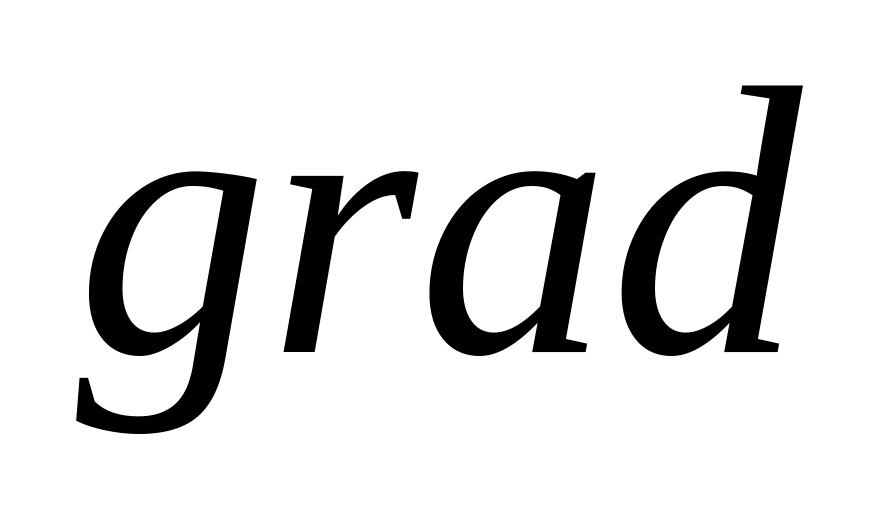
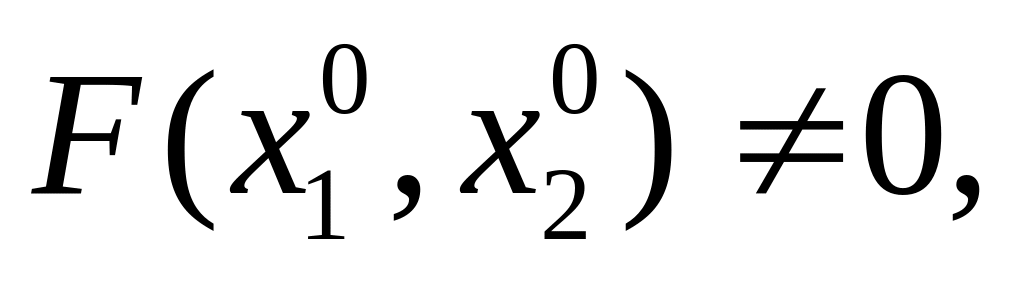
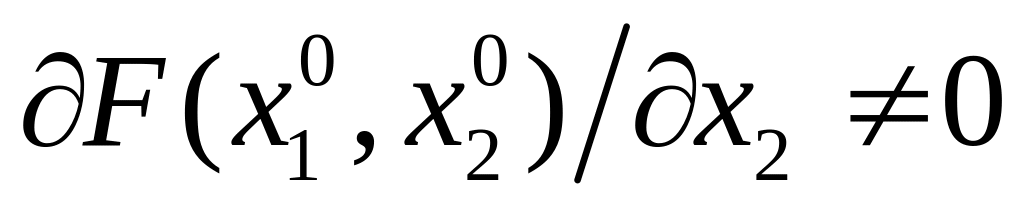4. и непрерывна в точке

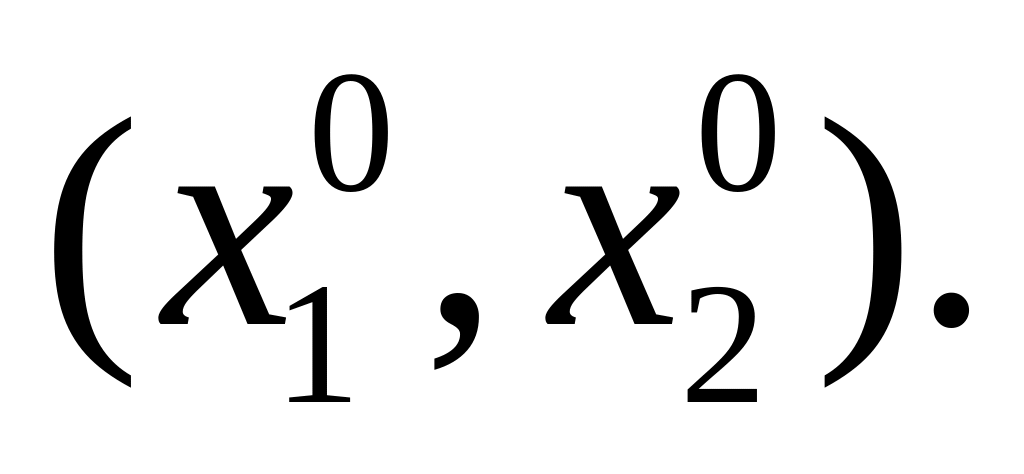
Тогда существуют числа такие, что для любого значения существует единственное значение такое, что т.е. существует единственная функция которая:

а) удовлетворяет условию

для всех

б) для всех

в)

г) дифференцируема (и, значит, непрерывна) в для всех таких, что

Доказательство этой теоремы является необязательным и поэтом у не приводится.

Теорема даёт достаточное условие однозначной локальной разрешимости уравнения относительно переменной при фиксированной переменной Теорема представляет собой нелинейное локальное обобщение факта однозначной глобальной разрешимости линейного уравнения относительно переменной при фиксированной переменной Достаточным условием такой однозначной глобальной разрешимости является условие (обобщением которого является условие 4) теоремы. Действительно при уравнение имеет единственное решение