О перации над множествами.

Объединение А и В – множество С, элементы которого принадлежат хотя бы одному из множеств А и В. Обозначается С = А  В.

Пересечение А и В – множество С, элементы которого принадлежат каждому из множеств А и В. Обозначение С = А  В.

Разность множеств А и В – множество, состоящее из элементов множества А, не принадлежащих множеству В. Обозначается С = А \ В.

С_Е – дополнение множества А относительно множества Е, если А  Е и C_Е = Е \ A.

На числовой прямой интервал – -окрестность числа .

Пример. (-0,9; 1,1) – окрестность радиуса 1 точки 0,1.

2.8 Мера плоского множества

Криволинейная трапеция – фигура, ограниченная графиком >0, заданной на , прямыми , и отрезком оси между точками и .

Площадь криволинейной трапеции .

Если фигура ограничена сверху графиком функции , а снизу – графиком функции , то площадь этой фигуры вычисляют по формуле .

П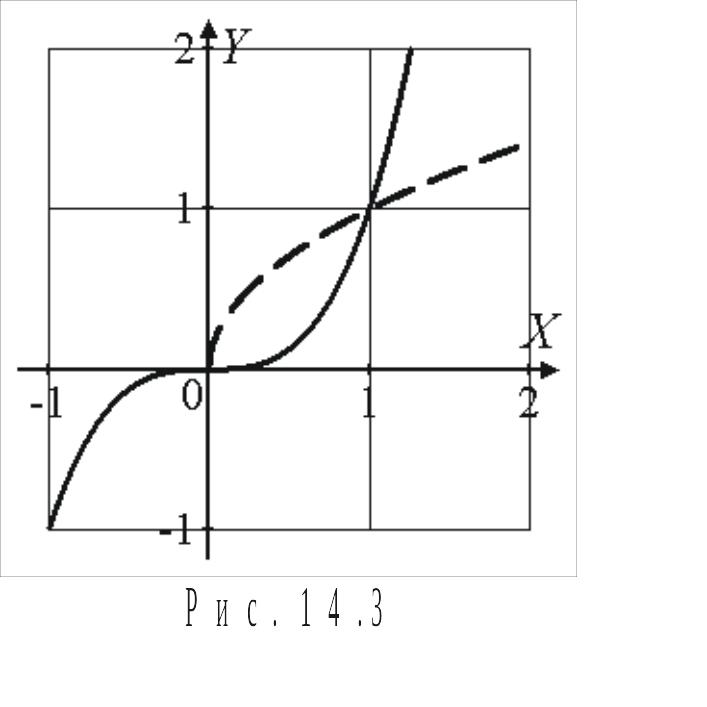 ример. Вычислить площадь фигуры, ограниченной линиями , .

1) Построим графики функций , .

2) Найдем пределы интегрирования. Для этого найдем абсциссы точек пересечения и . Имеем . Решим полученное уравнение

3) Вычислим площадь .

В общем случае фигуру следует разбить на трапеции и сложить их площади.

2.9 Числовые последовательности

Если каждому числу из множества натуральных чисел поставлено в соответствие вещественное число по правилу , то говорят, что задана числовая последовательность .

Число – предел последовательности , т.е. , если для любого числа >0 существует такой номер , что при всех выполняется неравенство .

Если существуют конечные пределы , , то:

1) , 2) , 3) , 4) ( ).

Если , то последовательность называют бесконечно малой.

Свойства б/м: 1) произведение б/м на ограниченную последовательность есть б/м; 2) сумма конечного числа б/м есть б/м; 3) произведение б/м есть б/м.

Если , то называют бесконечно большой.

Если – бесконечно малая, то – бесконечно большая, и наоборот.

1. ( ).	2. ( ).	3. ( ).
4. .	5. ( ).	6. ( ).
7. ( ).	8. ( ).	9. .
10. .	11. .	12. ( ).

Пример 1. .

Пример 2.

.

Пример 3.

.

Пример 4.

Пример 5.

.

2.10 Область сходимости степенного ряда

Степенной ряд имеет вид , – его коэффициенты. – ряд Маклорена.

Заменой , то от ряда всегда можно перейти к ряду Маклорена .

Интервал – интервал сходимости степенного ряда, – радиус сходимости, если при ряд сходится, а при расходится.

Формула Коши. Пусть . Тогда: 1) если , то ; 2) если , то ; 3) если , то .

Пример. Для : , . Отсюда .

Формула Даламбера. Пусть . Тогда: 1) если , то ; 2) если , то ; 3) если , то .

Пример. Для : , .

Отсюда .

Пример. Найти интервал сходимости для .

Так как , то  . Отсюда .

Ряд сходится при: , или , или . Итак, интервал сходимости .

Если разложима в степенной ряд в окрестности точки , то коэффициенты степенного ряда вычисляются по формуле (коэффициенты Тейлора-Маклорена).

Пример. Получить три ненулевых члена разложения в степенной ряд функции в точке .

Вычислим . При , , .

При , , .

При , , .

Итак, .