2.5 Дифференциальное исчисление фнп
– линия
уровня
.
Пример.
Найти линии уровня функции
.
Линии уровня данной
функции – это кривые
на плоскости
.
Преобразуем
или
.
Это семейство окружностей с центром в
точке
радиуса
(
).
– частная
производная
по
в точке
.
.
– частная
производная
по
в точке
.
Обозначения:
,
,
;
,
,
.
При дифференцировании по одной переменной – другие считаются постоянными!
Пример.
Для
:
,
.
Градиент
–
вектор частных производных. Для
в
– это
.
Пример.
Найти градиент функции
в точке
.
1)
Найдем частные производные функции
:
,
.
2)
Вычислим в точке
:
,
.
3)
Составим из полученных значений градиент
.
Частные производные высших порядков – производные от производных!
Пример. Найти все частные производные второго порядка функции .
1)
Найдем частные производные первого
порядка:
,
.
2) Найдем частные производные второго порядка:
,
,
,
.
Необходимое
условие экстремума в
точке
:
.
Достаточные условия экстремума:
1)
если
,
(
),
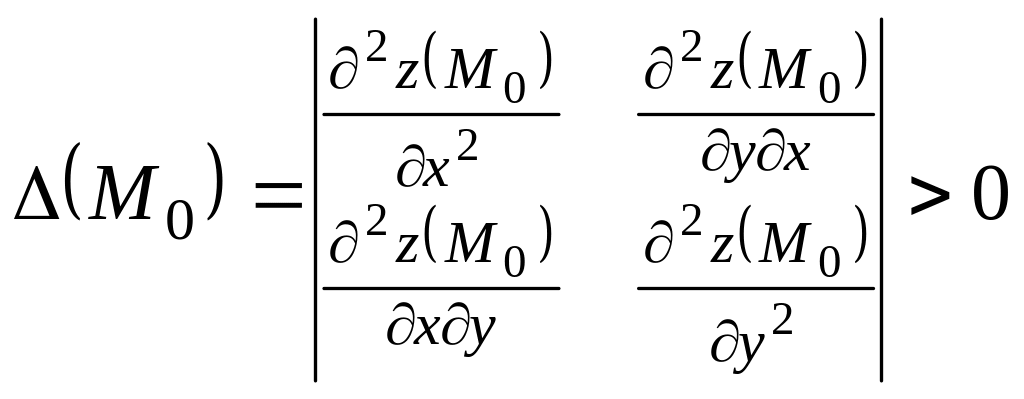то в точке
функция имеет минимум (максимум),
2)
если
,
то в точке
нет
экстремума.
Пример.
Найти
точки экстремума функции
.
1)
Найдем частные производные:
,
.
2)
Решаем:
Таким
образом, стационарные точки:
,
.
3)
Вычислим частные производные второго
порядка:
,
,
,
.
Тогда
.
4) Вычислим значения определителя в стационарных точках.
В
точке
,
следовательно, в точке
нет экстремума. В точке
,
,
следовательно,
– точка минимума.
2.6 Свойства определенного интеграла
– первообразная для функции
,
если
.
Совокупность всех первообразных –
неопределенный интеграл
–
=F(x)+C.
Таблица первообразных основных элементарных функций
1.
|
11.
|
2.
|
12.
|
3.
|
|
4.
|
13.
|
5.
|
14.
|
6.
|
|
7.
|
15.
|
8.
|
16.
|
9. |
17.
|
10. |
18.
|
.
.
.
.
,
,
.
,
.
.
,
,
.
.
.
.
,
.
,
,
.
.
,
,
.
.
Пример.
Метод подстановки
.
Следствие.
.
Пример.
.
Пример.
.
Интегрирование по частям
.
1) в
,
,
,
(
– многочлен степени
)
выбирают
,
любая из оставшихся частей будет
;
2) в
,
,
,
,
выбирают
,
любая из оставшихся частей будет
;
Пример.
.
Пример.
.
Определенный
интеграл
,
где
– любая первообразная для
(вычисляем неопределенный интеграл, а
потом применяем эту формулу). Пример.
.
Свойства
определенного интеграла 1.
.
2.
.
3.
.
4.
.
5.
.
2.7 Элементы теории множеств
Множество М – объединение в единое целое определенных различимых объектов а, которые называются элементами множества: а М
Множество, не содержащее элементов, называется пустым и обозначается .
Если все элементы
множества А являются также элементами
множества В, то говорят, что множество
А включается
(содержится)
в множестве В:
.
При этом А – подмножество для В.