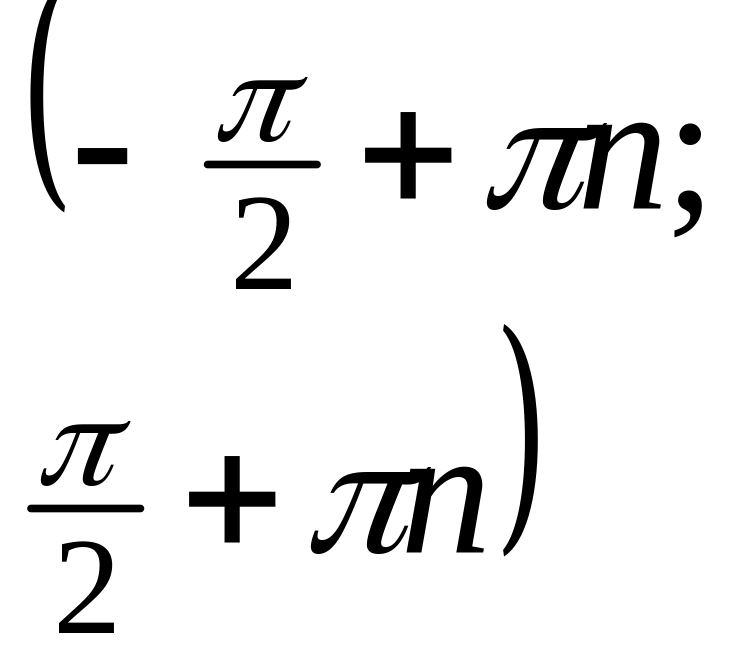2. Математический анализ
2.1 Функции: основные понятия и определения
Определение.Если
каждому элементу
из множества
по определенному правилу
поставлен в соответствие один элемент
из множества
,
то говорят, что на
(это
)
задана функция
с множеством значений
из
.
Определение. Пусть
задана на
,
а
задана на
и имеет область значений
.
Тогда
,
заданную на
,
называют суперпозицией функций
(сложной функцией).
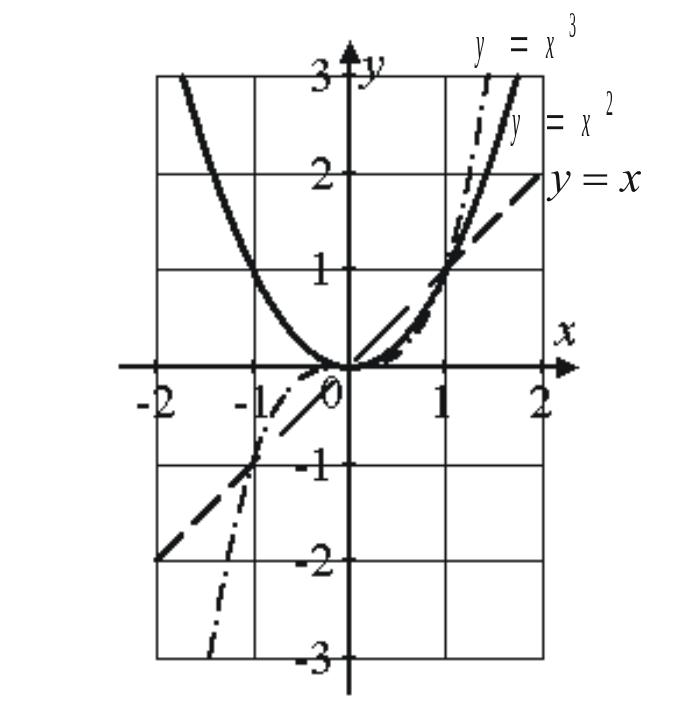
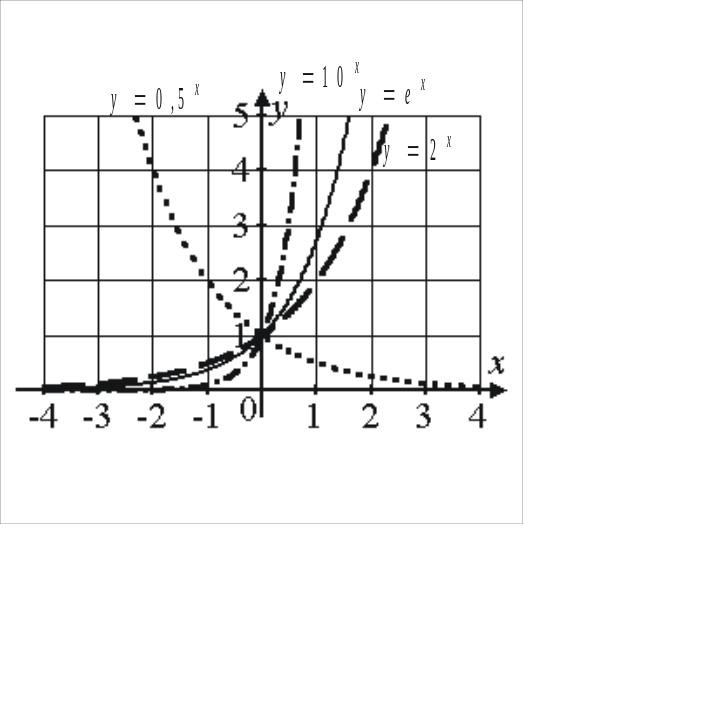
Основные элементарные функции::
(
)
– степенная,
(
,
)
– показательная,
(
,
)
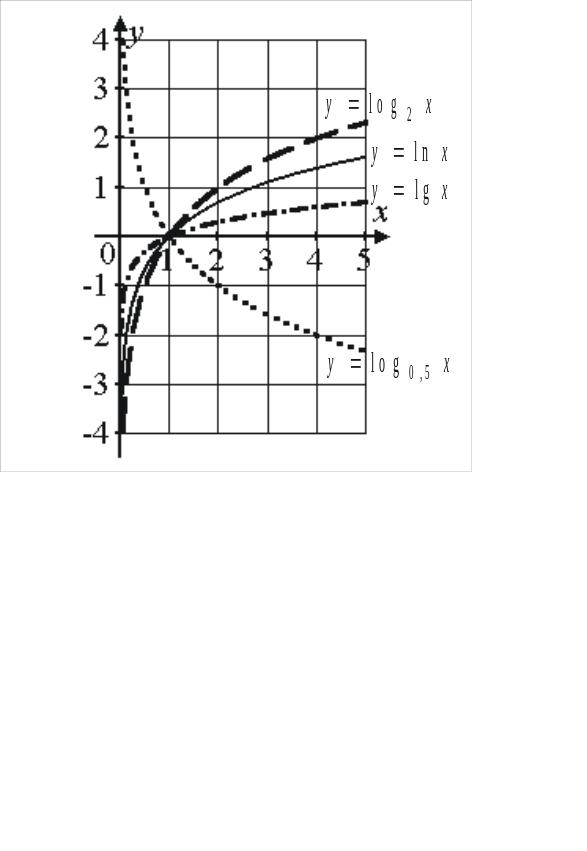
– логарифмическая,
,
,
,
– тригонометрические,
,
,
,
– обратные тригонометрические.
№ п/п |
Обозначение |
Область определения |
Область значений |
Монотонность |
Свойства |
График |
Степенная функция |
||||||
1. |
|
|
,
если
|
возрастает на , если нечетно |
нечетная, если – нечетно, непериодическая |
|
|
убывает
на
|
четная, если – четно, непериодическая |
||||
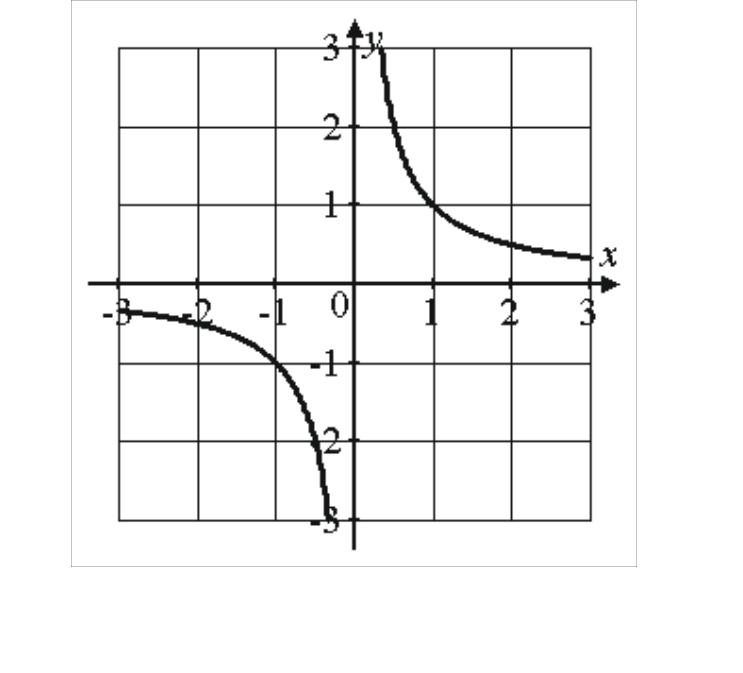
2. |
|
|
если – нечетно |
убывает
на
и на
|
нечетная, если – нечетно, непериодическая |
|
, если – четно |
возрастает на и убывает на , если – четно |
четная, если – четно, непериодическая |
|
|||
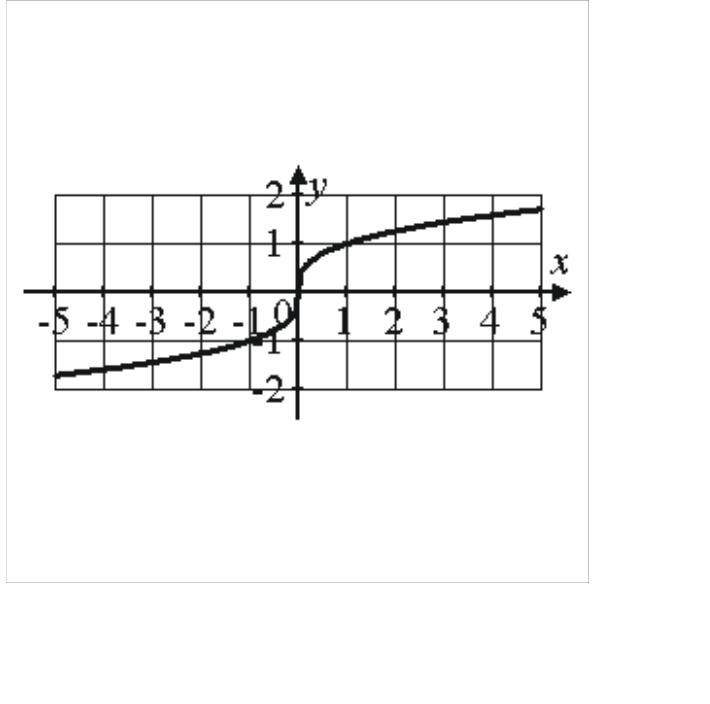
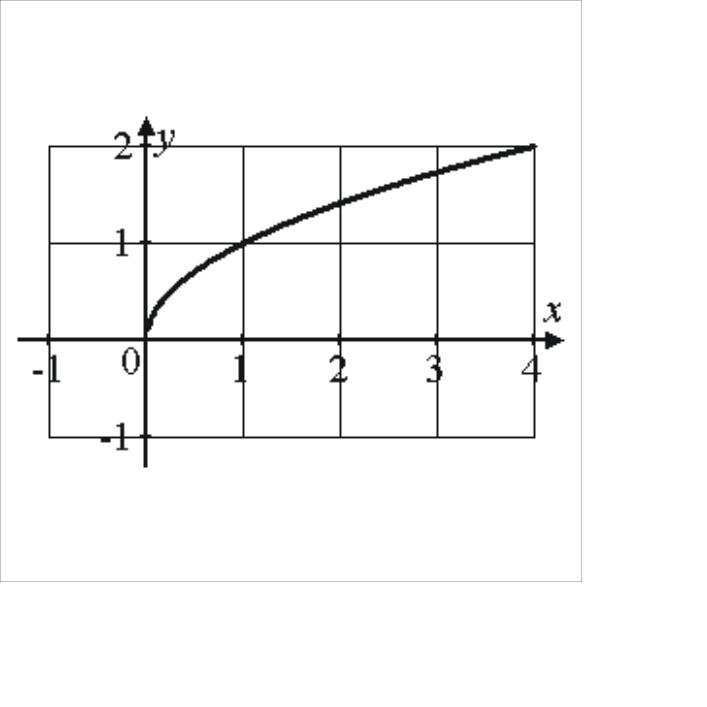
3. |
|
, если – нечетно |
, если – нечетно |
возрастает на интервале , если – нечетно |
нечетная, если – нечетно, непериодическая |
|
, если – четно |
, если – четно |
возрастает на , если – четно |
ни четная, ни нечетная, если – четно, непериодическая |
|
||
Показательная функция |
||||||
4. |
, |
|
|
возрастает
на
,
если
|
не является ни четной, ни нечетной, непериодическая |
|
убывает
на
,
если
|
||||||
Логарифмическая функция |
||||||
5. |
|
|
|
возрастает
на
|
не является ни четной, ни нечетной, непериодическая |
|
убывает на
,
если
|
||||||
нечетно
,
если
– четно
,
возрастает на
,
если
четно
,
если
– нечетно
,
,
если
№ п/п |
Обозначение |
Область определения |
Область значений |
Монотонность |
Свойства |
График |
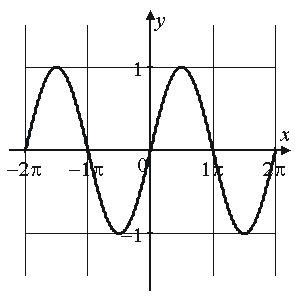
Тригонометрические функции |
||||||
6. |
|
|
|
возрастает
на
|
нечетная,
периодическая с периодом
|
|
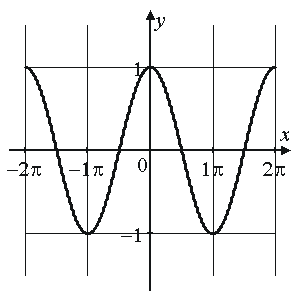
7. |
|
|
|
возрастает
на
|
четная, периодическая с периодом |
|
8. |
|
|
|
возрастает
на
|
нечетная,
периодическая с периодом
|
|
9. |
|
|
|
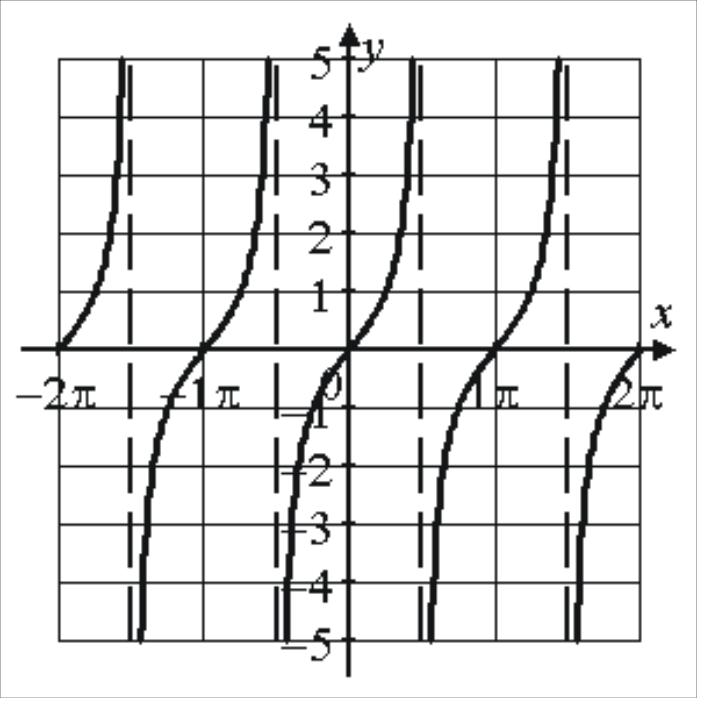
убывает
на
|
периодическая с периодом , нечетная |
|
Обратные тригонометрические функции |
||||||
10. |
|
|
|
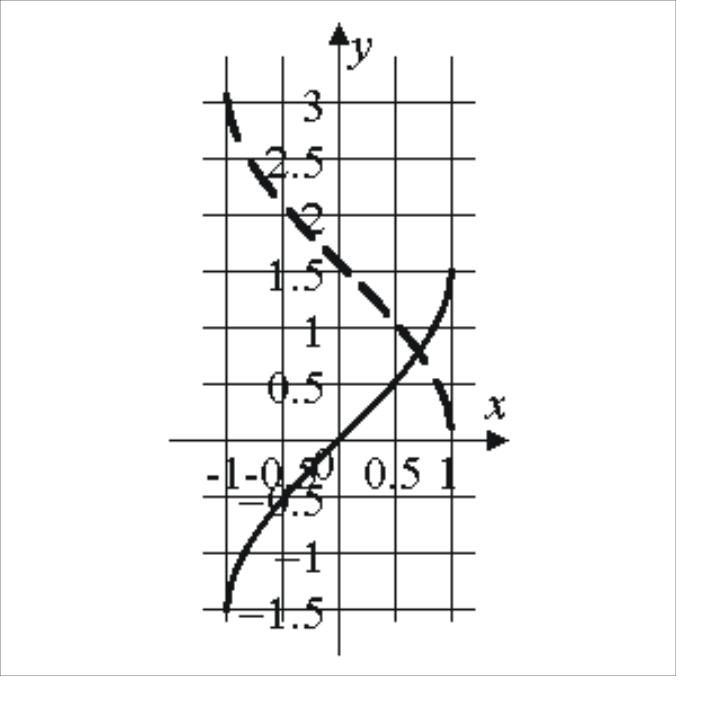
возрастает на |
нечетная, непериодическая |
|
11. |
|
|
|
убывает на |
не является ни четной, ни нечетной, непериодическая |
|
12. |
|
|
|
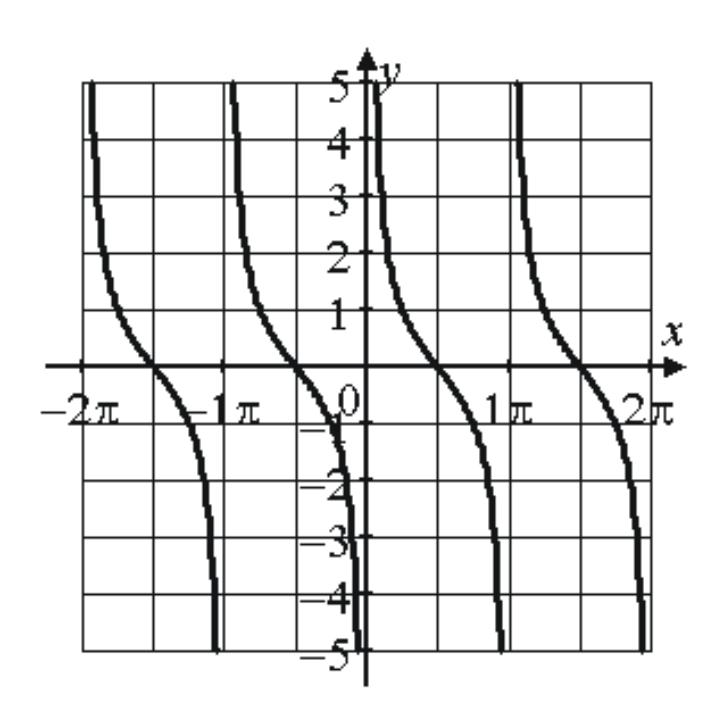
возрастает на |
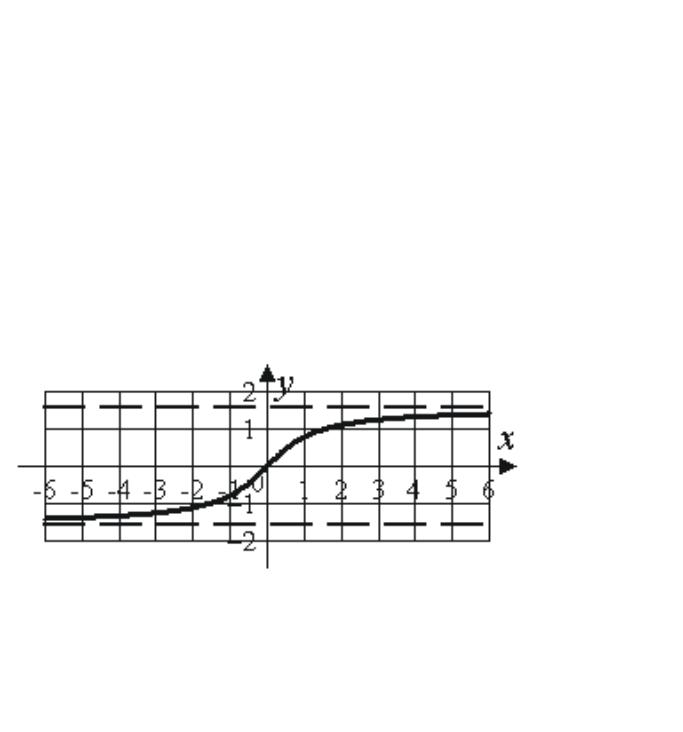
нечетная, непериодическая |
|
13. |
|
|
|
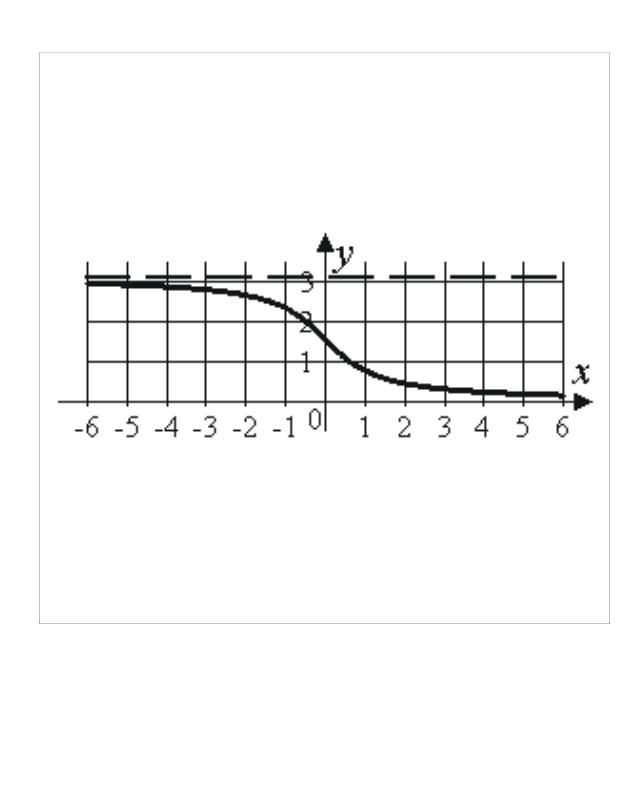
убывает на |
не является ни четной, ни нечетной, непериодическая |
|
,
убывает
на
,
,
убывает
на
,
,
,
