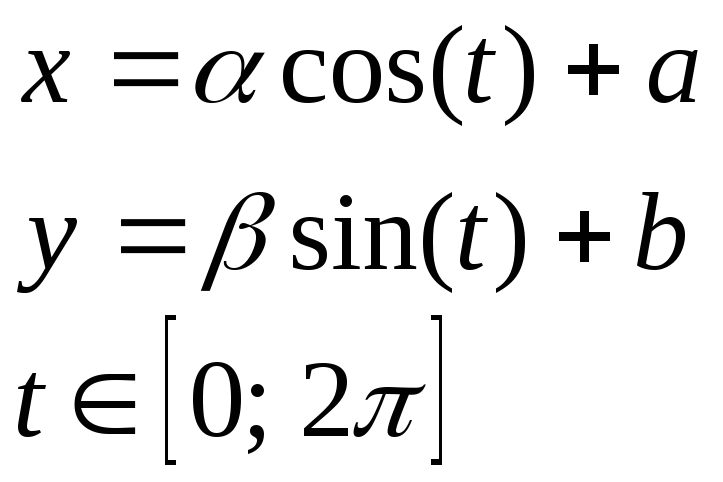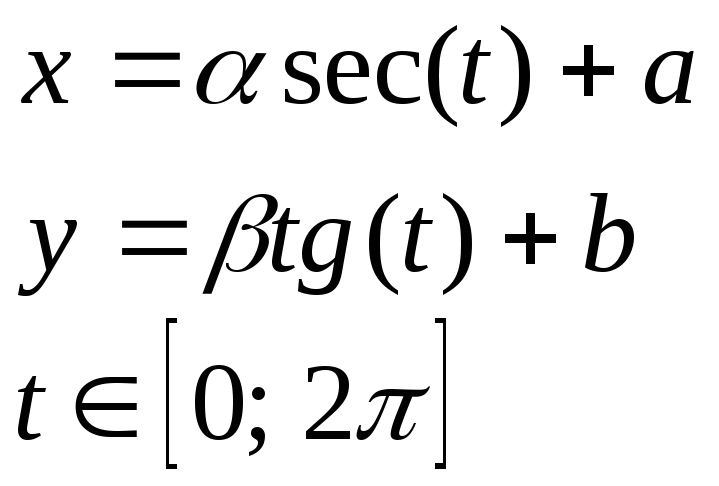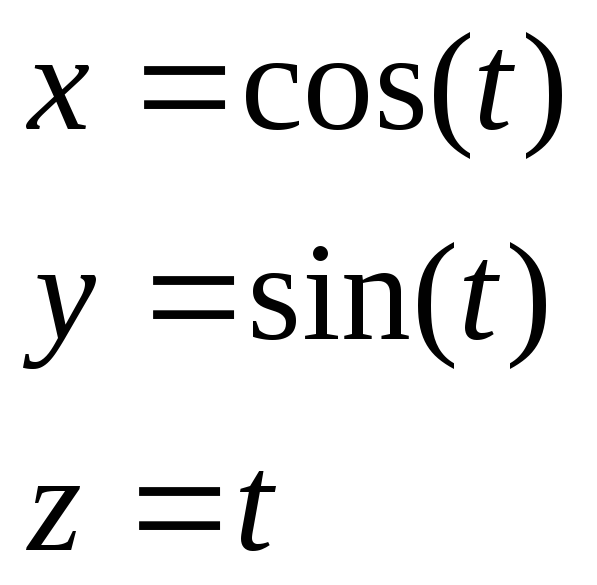Кривые в пространстве

Министерство образования и науки Российской Федерации

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»

кафедра математического обеспечения ЭВМ

Реферат

по дисциплине «Компьютерная графика»

«Представление пространственных форм: пространственные кривые»

Выполнил: Рыжок М.С. гр.3341

Проверил: Герасимова Т.В.

Санкт-Петербург 2007 г

Представление пространственных форм.

Пространственные кривые

За последние десятилетия компьютерная графика претерпела значительные изменения и в настоящее время представляет собой важнейшую дисциплину для специалистов во многих областях знания и, в частности, для проектировщиков электронных устройств, инженеров, математиков, химиков, художников и кинематографистов. В это время были в совершенстве разработаны прежние концепции машинной графики, а также предложены новые идеи. Однако основополагающие математические понятия остались неизменными. Глубокое овладение базовыми математическими концепциями до сих пор остается базовым ключом к пониманию и дальнейшему развитию компьютерной графики.

Одним из таких базовых разделов является получение раздел, исследующий изображения математических кривых на плоскости и в пространстве.

Существует множество способов построения кривых вручную с помощью карандаша, ручки, кисточки и разнообразных инструментов: линейки, лекала, циркуля, плаза, шаблона и.т.д. Каждый инструмент служит своей определенной цели, но среди них нет ни одного универсального. Так и в компьютерной графике кривые строятся с помощью различных методов и инструментов.

Кривая может быть представлена совокупностью точек. Если точки расположены близко друг от друга, то, соединяя их отрезками прямой, мы получим изображение кривой. Если плотность точек невелика, то получается довольно плохое представление кривой.

Хотя, как показано выше, кривые могут быть хорошо представлены совокупностью точек, аналитическое представление во многих отношениях предпочтительнее. Его преимущества – точность, компактность записи и простота вычисления промежуточных точек. Аналитическое представление позволяет без труда определить наклон и радиус кривизны, а при точечном представлении для этого требуется довольно сложная процедура – численное дифференцирование. Сравните объем памяти для точечного представления окружности с 32 точками на ней и аналитическое представление – координаты центра и радиус. При аналитическом представлении можно определить координаты любой точки, а при точечном нужна интерполяция, причем ее результат может не принадлежать кривой.

Опыт показывает, что аналитически заданные кривые легче изобразить на рисунке. Аналитическое представление выгоднее, если для удовлетворения заданному критерию необходимо постоянно изменять форму кривой. Ниже рассматриваются аналитические методы представления двумерных и трехмерных кривых.

Часто требуется получить аналитическое представление кривой, первоначально заданной точками. С математической точки зрения это проблема интерполяции. Для того, чтобы провести кривую через все заданные точки, применяется метод кусочно-линейной аппроксимации или сплайны. Для этого требуется определить коэффициенты полинома некоторой степени. Вид функции будет зависеть от степени полинома и граничных условий. Если же точки – только приблизительные значения величин, то нужна кривая, верно задающая направление. В этом случае используют метод наименьших квадратов.

Математически кривая может быть представлена в параметрической и непараметрической форме. Непараметрическая кривая задается в явной или неявной форме. Явное параметрическая кривая имеет вид z = f(x, y). Пример – уравнение прямой z = ax+by+c. При этом одной паре значений (x;y) соответствует одно значение z. Поэтому замкнутые и многозначные кривые, например окружность, так представить нельзя. Выручает неявное представление кривой: f(x, y, z) = 0. Например, для окружности – x²+y²+z² = R², где R – радиус окружности.

Как явное, так и неявное представление осезависимо, т.е. сложность обработки зависит от выбора системы координат. Кроме того, если точки на такой кривой вычисляются с равномерным приращением по x, y или z, то они, как правило, не будут равномерно распределены вдоль кривой. Это может повлиять на качество и точность графического изображения. Тем не менее, непараметрическое представление бывает полезно.

В параметрическом представлении каждая координата точки кривой представлена как функция одного аргумента. Значения аргумента задает координатный вектор точки на кривой. Для трехмерной кривой с параметром t координаты точки равны:

X = x(t)

Y = y(t)

Z = z(t)

Чтобы получить непараметрическую форму, нужно исключить параметр t из трех уравнений и вывести одно в переменных x, y и z.

Параметрическая форма позволяет вывести замкнутые и многозначные кривые. Так как точка на параметрической кривой определяется только значением параметоа, эта форма не зависит от выбора осей координат. Конечные точки определяются диапазоном изменения параметра. Часто бывает удобно нормализовать его 0<t<1.

Таблица: Некоторые кривые и их представления:

Имя кривой	Непараметрическое представление	Параметрическое представление	Рисунок
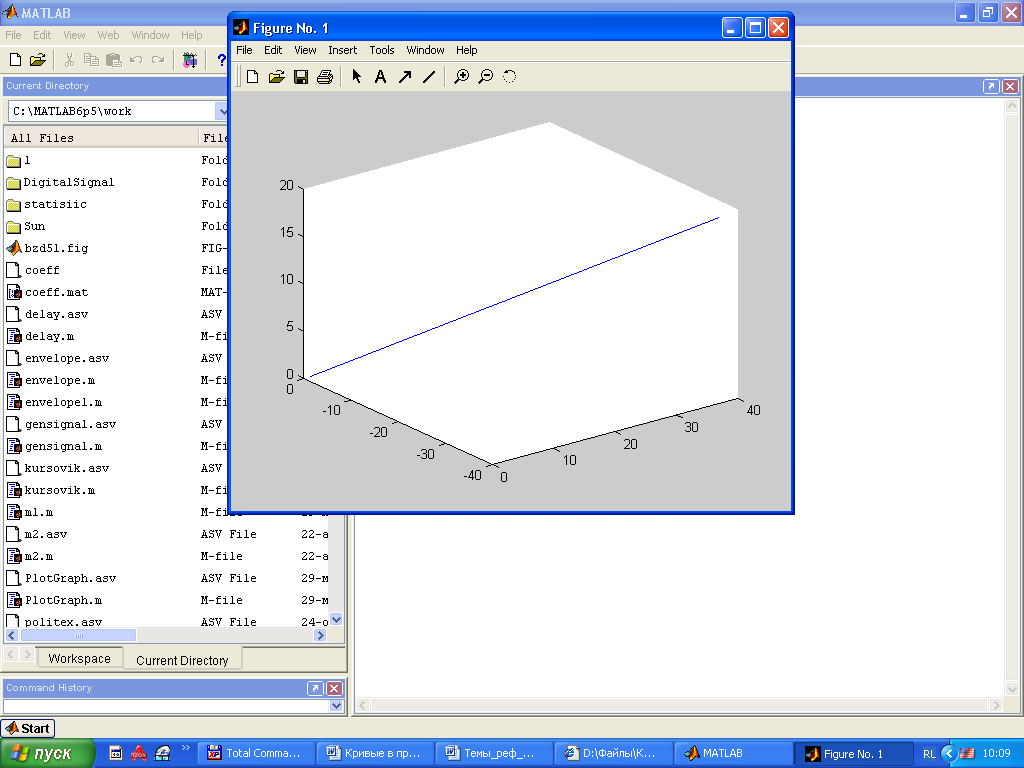
Прямая	z = ax+by+c Ax+By+Cz+D=0	x = a1t+a2 y= b1t+b2 z = c1t+c2
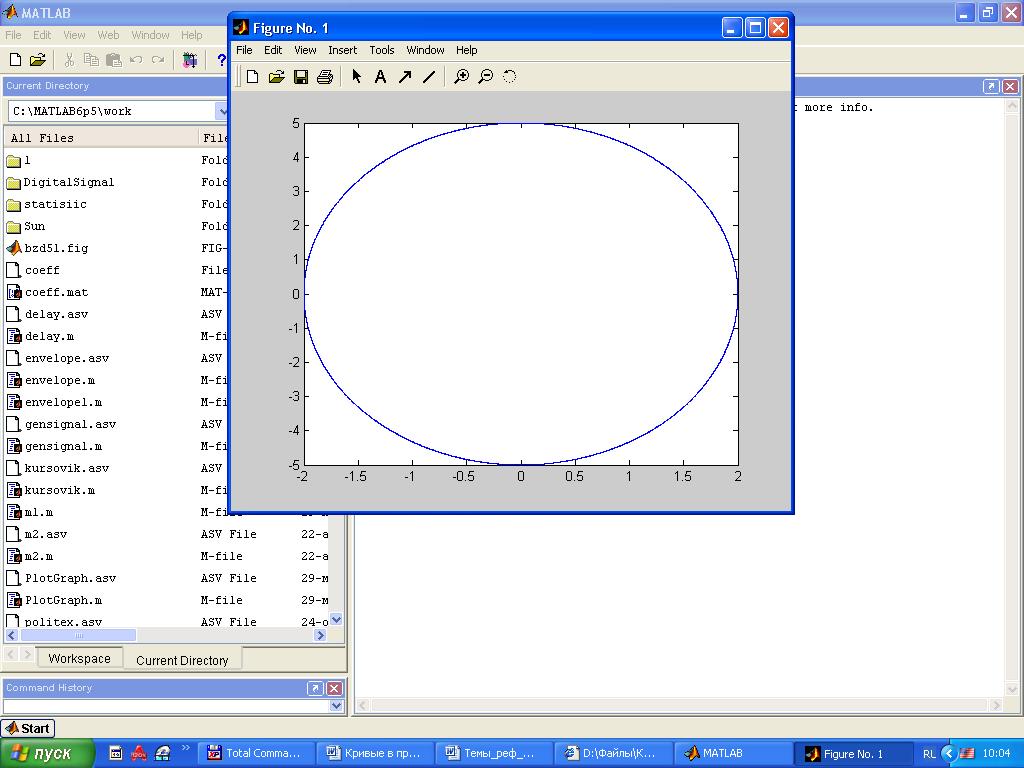
Окружность	(x-a)2+(y-b)2=R2	x = cos(t)+a y = sin(t)+a z = const
Эллипс (на плоскости)
Гипербола
Парабола	y2 = 2px
Спираль
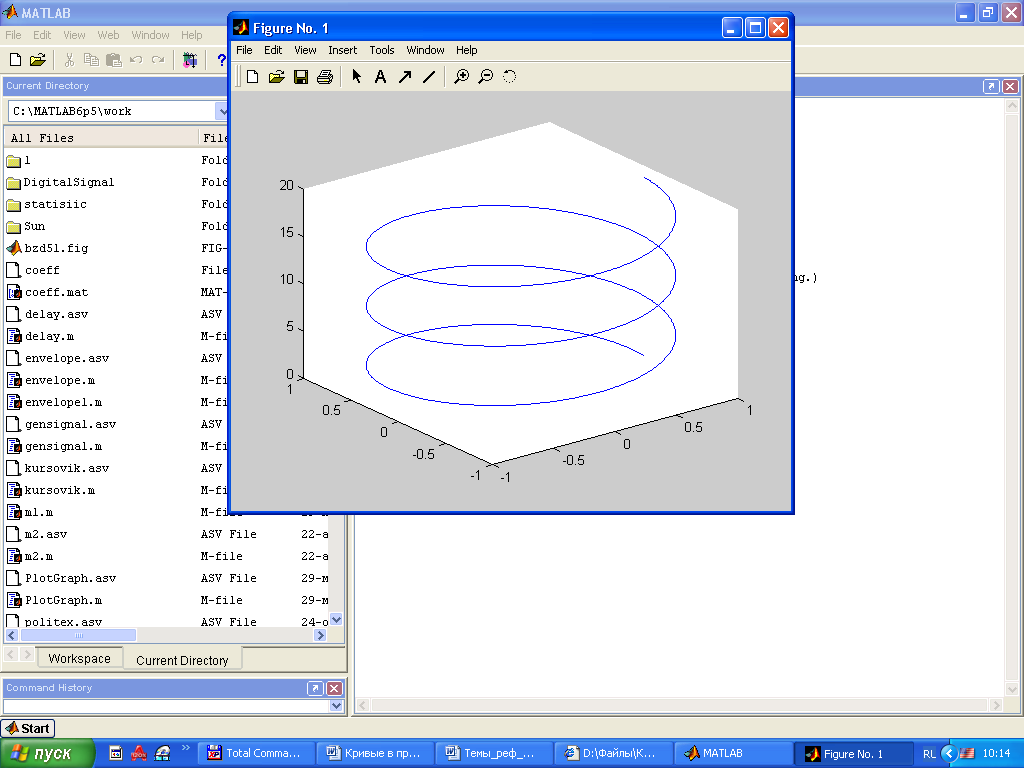
Винтовая линия

Кубические сплайны

В промышленном производстве, например, судо-, автомобиле- или авиастроении, окончательная форма в реальном или близком к нему масштабе определяется в процессе доводки. Автоматизация этого процесса представляет собой большой интерес для компьютерной графики. Форма математического сплайна представляет собой форму физического сплайна, т.е гибкой деревянной или пластмассовой линейки, проходящей через определенные точки. Для изменения формы сплайна используются свинцовые грузики. Меняя их количество и расположение, получившуюся кривую пытаются сделать как можно более гладкой.

Если рассмотреть физический сплайн как тонкую длинную рейку, его форма (отклонение y) определяется уравнением Эйлера для момента изгиба вдоль рейки , где Е – модуль Юнга, зависящий от свойств материала рейки, I – момент инерции, определяемы формой кривой, R(x) – радиус кривизны, который рассчитывается как 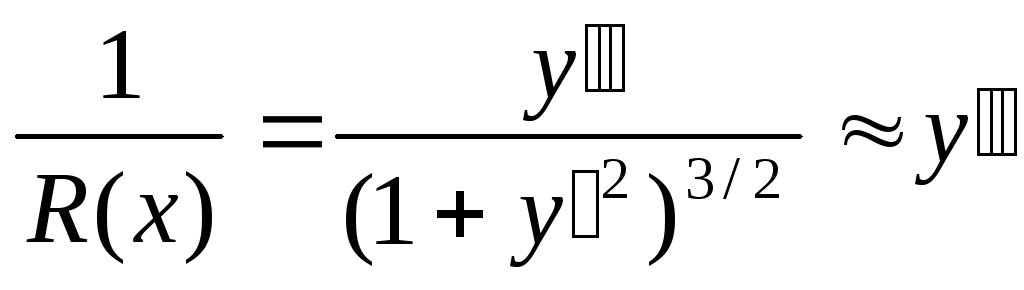, где штрих обозначает производную по x – расстояние вдоль рейки, а y – отклонение рейки. Уравнение Эйлера принимает форму: . Пусть грузики действуют как простые подпорки, тогда момент изгиба между ними изменяется линейно. Подставляя M(x) = Ax+B в уравнение и интегрируя по x, получаем:

y = A₁x³+B₁x²+C₁x+D₁

Таким образом, форма сплайна задается кубическим полиномом.

В общем случае математический сплайн – это кусочный полином степени К с непрерывной производной степени К-1 в точках соединения сегментов. Так, например, кубический сплайн имеет в точках соединения непрерывность второго порядка. Кусочные сплайны из многочленов невысокого порядка очень удобны для интерполяции кривых, так как они не требуют больших вычислительных затрат и не вызывают отклонений, свойственных многочленам высокого порядка. По аналогии с физическими сплайнами часто используется серия кубических сегментов, причем каждый сегмент проходит через 2 точки. Кубический сплайн удобен еще и тем, что это кривая наименьшего порядка, допускающая точки перегиба и изгиб в пространстве.

Уравнение одного сегмента кубического сплайна выглядит так:

, где t₁ и t₂ – значение параметра в начале и конце сегмента, P(t) = [x(t), y(t), z(t)] – векторнозначная функция, ее составляющие – декартовы координаты точек сплайна.

Рисунок 1. Один сегмент сплайнв

Каждая составляющая имеет вид, похожий на P(t), то есть:

Постоянные коэффициенты Bi вычисляются, исходя из четырех граничных условий. Запишем уравнение сегмента в виде:

P(t) = B₁+B₂t+B₃ t²+B₄ t³

Пусть P1 и P2 – векторы концов сегмента. Пусть также P1’ и P2’ , производные по t, будут касательными векторами в концах сегмента. Дифференцируя уравнение сегмента, получим:

Предположим без потери общности, что t₁ = 0 и применим граничные условия:

P(0) = P1

P(t₂) = P2

P’(0) = P1’

P’(t₂) = P2’

Получим четыре уравнения для неизвестных B_i

Решения для Bi имеют вид

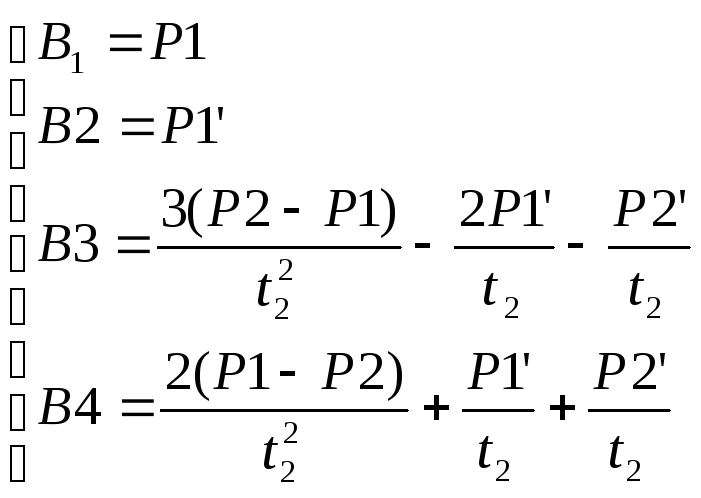
Величины B1, B2, B3 и B4 задают сегмент кубического сплайна. Очевидно, что форма сегмента зависит от положения касательных векторов на концах сегмента. Далее заметим, что в результате присутствует значение параметра t = t₂. Подставляя значения коэффициентов Bi в уравнение сегмента, получаем ее явное представление.

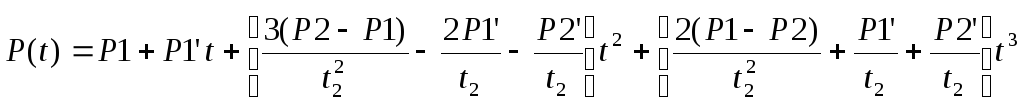(1)

Это уравнение для одного сегмента. Чтобы получить кривую целиком, нужно соединить множество сегментов. На рисунке 3 показано соединение двух соседних сегментов. Если известны векторы P1, P2, P3, касательные P1’, P2’, P3’ и значения t2 и t3, то форма каждого сегмента определяется из уравнения (1). Однако маловероятно, что известен касательный вектор P2’ в точке соединения. К счастью, его можно вывести из условия непрерывности.

Рисунок 2 Соединение двух сегментов сплайна

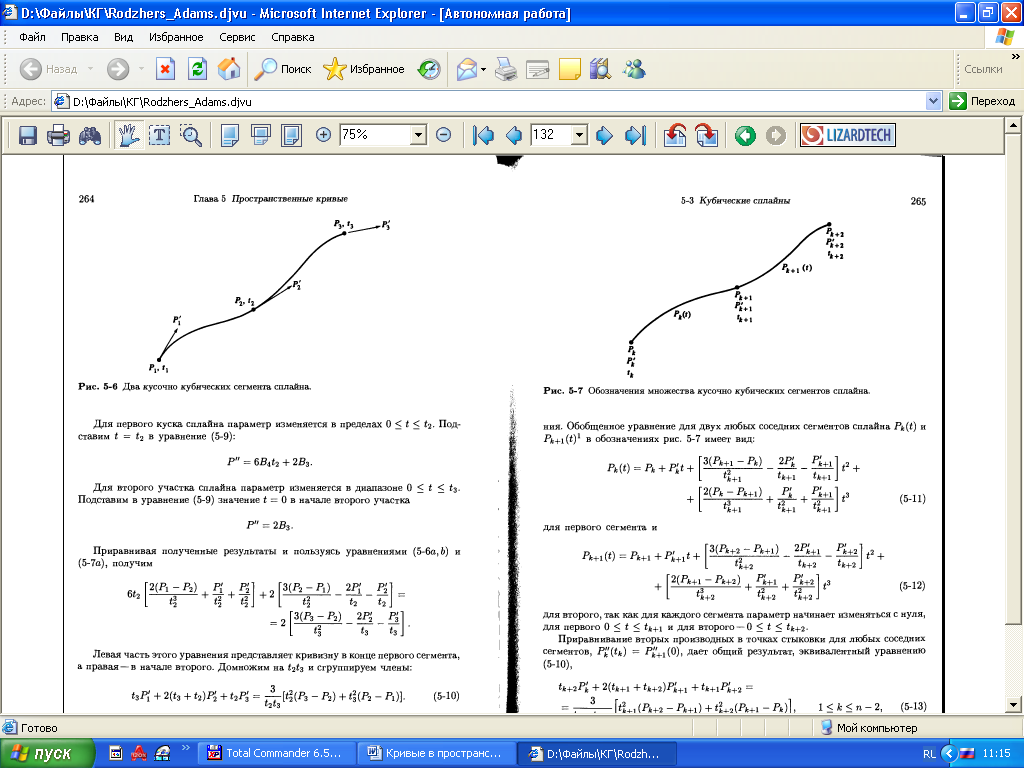
Вспомним, что кусочный сплайн степени K имеет непрерывность степени K-1 в точках соединения, непрерывность кубического сплайна равна 2. Для этого должна быть непрерывна вторая производная P’’(t) или кривизна линии. Дважды продифференцировав уравнение сегмента, получим:

Для первого куска сплайна t меняется от 0 до t2 и поэтому P’’ = 2B₃+6B₄t₂

Для второго участка сплайна t меняется от 0 до t3. Подставляя t = 0: P’’ = 2B3

Приравнивая полученные результаты и пользуясь явными уравнениями, в итоге получаем:

Отсюда находится неизвестный касательный вектор P1’ в точке соединения.

Обобщая полученную формулу для n точек и, соответственно, n-1 сегмента, получаем: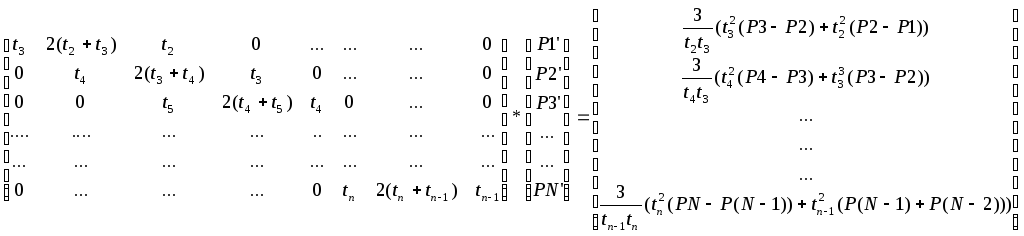

Матрица в левой части неквадратная, т.к имеется только n-2 уравнений для ее векторов. Ее нельзя обратить и получить решение для P’. Но если предположить, что известны касательные векторы на концах кривой, P1’ и PN’, проблема разрешается. Теперь система имеет вид:

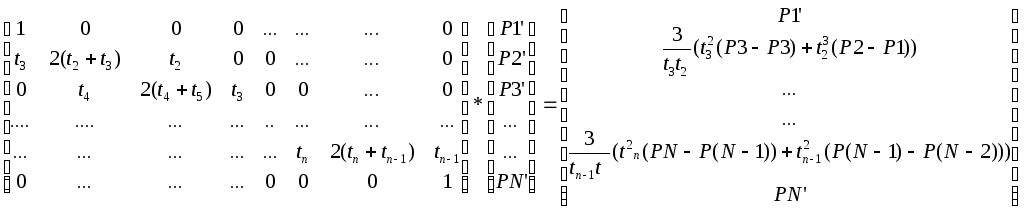
Теперь матрица не только квадратная, но и трехдиагональная, что снижает затраты на решение системы.

Уравнение сегмента сплайна в матричной форме выглядит как:

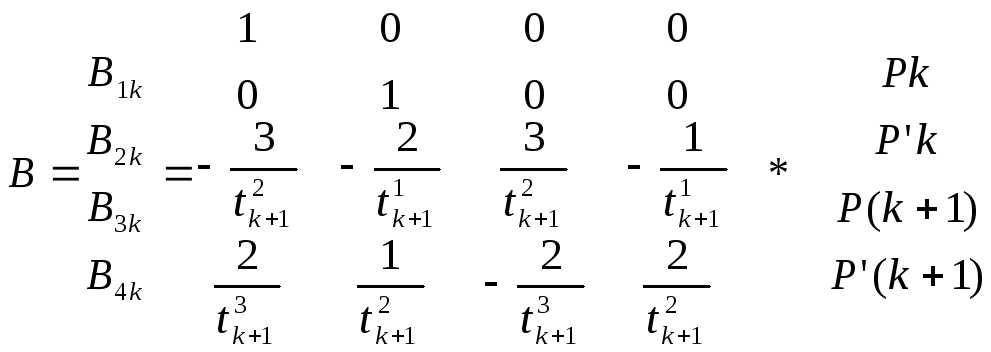
Кривые Безье

До сих пор мы обсуждали, как провести кривую через заданное множество точек. Рассмотренные методы во многих случаях дают прекрасные результаты и особенно удобны для описания формы, основа которой получена в результате экспериментов или математических расчетов. Существует, однако, и другой класс задач, когда решение зависит как от функциональных, так и от эстетических требований, например, дизайн поверхности машины или составные части мотора. Кроме количественных критериев здесь требуется учет практического опыта и часто требуется интерактивное вмешательство разработчика.

Рассмотренные выше кубические сплайны неудобны для интерактивной работы. Направление и величина касательных не дают необходимого интуитивного понятия о кривой. Неочевидна связь между набором чисел и формой кривой.

Пьер Безье предложил другой способ создания кривых и поверхностей любой формы. Кривая Безье задается многоугольником или ломаной, как показано на рисунке 4.

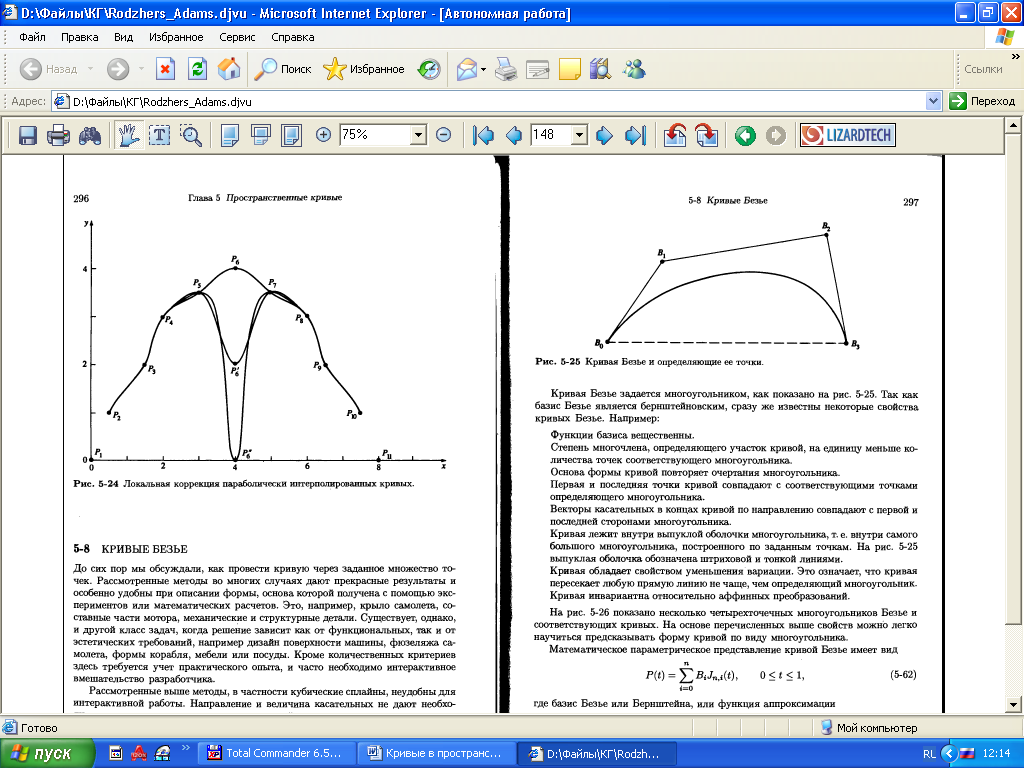Рисунок 3. Кривая Безье.

Кривая начинается и заканчивается в начальной и конечной точке ломаной, а звенья служат касательными в соответствующих точках. Можно научиться предсказывать форму кривой по форме многоугольника.

Математическое параметрическое представление кривой Безье имеет вид

, где J_n,I – многочлен Бернштейна

Так как базис Безье является бернштейновским, сразу же становятся известными некоторые свойства кривых Безье:

• Функции базиса вещественны

• Степень многочлена, определяющего участок кривой на 1 меньше количества точек соответствующего многоугольника

• Основа формы кривой повторяет очертания многоугольника

• Кривая лежит внутри выпуклой оболочки многоугольника, т.е. внутри самого большого многоугольника, построенного по заданным линиям.

• Кривая пересекает любую прямую линию не чаще, чем управляющий многоугольник.

• Кривая инвариантна относительно аффинных преобразований

Рисунок 4 Кривые Безье для кубических функций

Приложение

Функция, вычисляющая значение для построения кривой Безье и результат ее работы

Построена автором реферата

void BezieLine(unsigned int order, float (*P)[3])

{

if (order < 2)

return;

int i, j;

float *Tb, *Te;

float t = 0, z1 = 0, z2 = 0, z3 = 0;

Tb = (float*)malloc(order*sizeof(float));

Te = (float*)malloc(order*sizeof(float));

glBegin(GL_LINE_STRIP);

while (t <= 1)

{

for (i = 0; i <= order; i++)

{

Tb[i] = power(1-t, i);

Te[i] = power(t, order-i);

}

for (j = 0; j <= order; j++)

{

z1 = z1 + comb(order, j)*Tb[j]*Te[j]*P[j][0];

z2 = z2 + comb(order, j)*Tb[j]*Te[j]*P[j][1];

z3 = z3 + comb(order, j)*Tb[j]*Te[j]*P[j][2];

}

glVertex3f(z1, z2, z3);

z1 = 0; z2 = 0; z3 = 0;

t += 0.01;

}

glEnd();

}

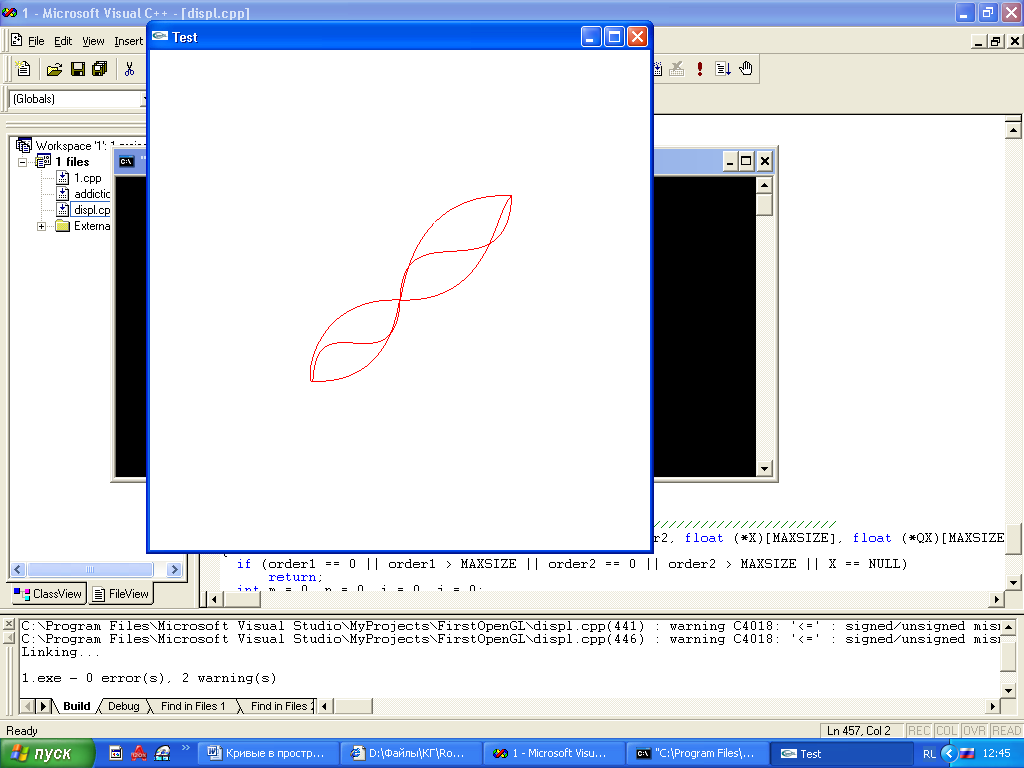
Рисунок 5. Визуализированный результат работы функции BezieLine “Узор” из кривых Безье

Список использованной литературы:

1. Д.Роджерс Дж.Адамс. Математические основы машинной графики, Москва, «Мир», 2001

2. Е.В.Шикин, А.В.Боресков. Компьютерная графика. Полигональные модели, Москва, «Диалог -МИФИ» 2001 г.