3. Вычисление моментов инерции сечений простой формы

Как указано ранее геометрические характеристики сложных сечений определяются путем расчленения их на ряд простых фигур, геометрические характеристики которых можно вычислить по соответствующим формулам или определить по специальным таблицам- Эти формулы получаются в результате непосредственного интегрирования выражений (8.5) — (10.5). Приемы их получения рассматриваются ниже на примерах прямоугольника, треугольника и круга.

ПРЯМОУГОЛЬНОЕ СЕЧЕНИЕ

Определим осевой момент инерции прямоугольника высотой h и шириной b -относительно оси z₁, проходящей через его основание (рис. 11.5,а). Выделим из прямоугольника линиями, параллельными оси Z₁, элементарную полоску высотой dy₁ и шириной b

Площадь этой полоски dF = bdy₁, расстояние от полоски до оси z равно z ₁. Подставим эти величины в выражение момента инерции (8.5):

Аналогичным путем для момента инерции относительно оси у₁ можно получить выражение

Для определения центробежного момента инерции J_yz выделим из прямоугольника линиями, параллельными осям z₁ и у₁ (рис. 11.5,6), элементарную площадку величиной dF = dz₁dy₁. Определим сначала центробежный момент инерции не всего прямоугольника, а лишь вертикальной полоски высотой h и шириной dz₁ расположенной на расстоянии z₁ от оси у₁.

Для случая когда оси проходят через центр тяжести:

Определим теперь осевые моменты инерции прямоугольника относительно осей у и z, проходящих через центр тяжести параллельно сторонам прямоугольника (рис. 12.5). Для этого случая пределы интегрирования будут от у — — -у

до y = -\--j. Следовательно,

Центробежный момент инерции прямоугольника относительно осей у и z (рис. 11.5) равен нулю, так как эти оси совпадают с его осями симметрии.

ТРЕУГОЛЬНОЕ СЕЧЕНИЕ

Определим осевые моменты инерции треугольника относительно трех параллельных осей z₁ z ₀ и z ₂ проходящих через его основание рис. 13.5,а), центр тяжести (рис. 13.5,6) и вершину (рис. 13.5,е).

Для случая, когда ось проходит через основание треугольника (рис. 13.5,а),

Для случая, когда ось проходит через центр тяжести треугольника параллельно его основанию (рис. 13.5,6),

В случае, когда ось проходит через вершину треугольника параллельно его основанию (рис. 13.5,е),

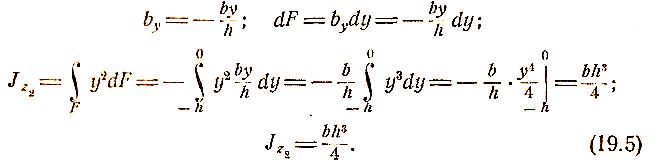
Момент инерции J_z2 значительно больше (в три раза), чем момент инерции J_z, так как основная часть площади треугольника более удалена от оси г₂, чем от оси z_x.

СЕЧЕНИЕ В ФОРМЕ КРУГА-

Определим осевой момент инерции круга относительно любой сен г, проходящей через его центр тяжести. Из рис. 16.5,а следует

Очевидно, что относительно любой оси, проходящей через центр круга, осевой момент инерции будет равен J_z и, следовательно,

По формуле (11.5) находим полярный момент инерции круга относительно его центра:

Полярный момент инерции элементарного кольца относительно центра круга dJ_p = p²dF, так как все элементарные площадки d (dF), из которых состоит это кольцо, расположены на одинаковом расстоянии р от центра круга. Следовательно,

Этот результат совпадает с полученным выше.

Моменты инерции (полярный и осевые) сечения, имеющего форму кругового кольца с наружным диаметром d и внутренним. d₀ (рис. 17.5), можно определить как разности между соответствующими моментами инерции наружного и внутреннего кругов.

Полярный момент инерции кольца на основании формулы (21.5)