- •Тема 1. Молекулярно-кінетична теорія ідеального газу.
- •Тема2.Основи термодинаміки.
- •Ізохорний процес .
- •Ізобарний процес .
- •Ізотермічний процес .
- •Тема 3.Електростатика.
- •Паралельне з’єднання конденсаторів.
- •Послідовне з’єднання конденсаторів.
- •Тема 4.Постійний струм.
- •. Енергетичні зони в кристалах
- •Розподіл електронів по енергетичних зонах. Валентна зона і зона провідності. Метали, діелектрики і напівпровідники
- •Власна провідність напівпровідників
- •§142. Домішкова провідність напівпровідників
- •Тема 5.Магнітостатика.
- •1. Магнітне поле прямолінійного провідника зі струмом.
- •2. Магнітне поле колового струму.
- •Тема 6.Електромагнітна індукція. Магнітні властивості речовини.
- •Тема 7.Основи теорії Максвела для електромагнітного поля.
- •Тема 8.Механічні і електромагнітні коливання.
- •Тема 9.Хвилі. Елементи хвильової оптики.
- •Смуги однакового нахилу
- •§2.1.4. Смуги однакової товщини
- •Кільця Ньютона
- •Дифракція Фраунгофера на одній щілині
- •Дифракція світла на дифракційній гратці
- •Тема 10. Основи квантової оптики.
- •Тема 11.Будова атома за Резерфордом-Бором.
- •Тема 12. Основи квантової механіки.
- •Тема 13.Елементи фізики атомного ядра.
Тема 7.Основи теорії Максвела для електромагнітного поля.
4.Рівняння Максвелла для електромагнітного поля в інтегральній та диференціальній формі.
І. Електричне
поле може бути як потенціальним
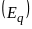 ,
так і вихровим
,
так і вихровим
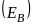 .
Тому напруженість сумарного поля
.
Тому напруженість сумарного поля
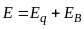 .
Оскільки циркуляція вектора
.
Оскільки циркуляція вектора
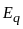 вздовж довільного замкненого контура
дорівнює нулю, то циркуляція вектора
сумарного поля
вздовж довільного замкненого контура
дорівнює нулю, то циркуляція вектора
сумарного поля
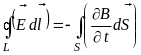 .
.
Це рівняння зв’язує значення із зміною вектора з часом і є виразом закону електромагнітної індукції.
Перше рівняння Максвелла вказує на те, що джерелами електричного поля можуть бути не тільки електричні заряди, але і змінні з часом магнітні поля.
ІІ. Узагальнена
теорема про циркуляцію вектора
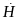 :
:
 .
.
Це рівняння показує, що магнітні поля можуть збуджуватись або рухомими зарядами, або змінними електричними полями.
ІІІ. Теорема
Остроградського-Гауса для потоку вектора
електричного зміщення
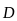 крізь довільну замкнену поверхню
,
що охоплює сумарний заряд
крізь довільну замкнену поверхню
,
що охоплює сумарний заряд
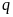 :
:
 .
.
Якщо
заряд розподілений всередині замкненої
поверхні з об’ємною густиною
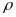 ,
то
,
то
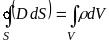 .
.
IV. Теорема Остроградського-Гауса для магнітного потоку крізь довільну замкнену поверхню :
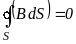 .
.
Отже, повна система рівнянь Максвелла в інтегральній формі має такий вигляд:
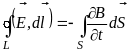 ,
,
 ,
,
 ,
,
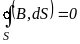 .
.
Величини, що входять в рівняння Максвелла, не є незалежними і між ними є такий зв’язок:
 ,
,
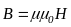 ,
,
 .
.
Зазначимо,
що до першого та четвертого рівняння
Максвелла входять лише основні
характеристики поля
і
,
а в друге і третє – лише допоміжні
величини
і
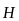 .
.
РОЗДІЛ III. Фізика коливань і хвиль.
Тема 8.Механічні і електромагнітні коливання.
5.Додавання гармонічних коливань однакового напрямку і однакової частоти.
Перш ніж розглядати додавання коливальних рухів, спинимось на способі зображення коливань за допомогою обертального вектора амплітуди.
Для цього із
довільної точки О,
яка вибрана на осі X,
під кутом
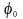 ,
що дорівнює початковій фазі коливань,
відкладемо вектор
,
що дорівнює початковій фазі коливань,
відкладемо вектор
 ,
модуль якого дорівнює амплітуді A
коливання (рис. 28).
,
модуль якого дорівнює амплітуді A
коливання (рис. 28).

Проекція вектора
на вісь OX
дорівнює зміщенню
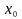 у момент початку відліку часу
у момент початку відліку часу
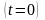 :
:
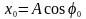 .
.
Обертатимемо
вектор амплітуди навколо осі O,
яка перпендикулярна до площини рисунка,
з кутовою швидкістю
 .
За проміжок часу t
вектор амплітуди повертається на кут
.
За проміжок часу t
вектор амплітуди повертається на кут
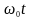 .
Проекція вектора
в цьому положенні на вісь ОХ
дорівнює:
.
Проекція вектора
в цьому положенні на вісь ОХ
дорівнює:
 .
.
За час Т,
що дорівнює періоду коливань, вектор
амплітуди повертається на кут
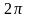 ,
а проекція його кінця зробить одне повне
коливання навколо положення рівноваги
O,
отже, обертовий вектор амплітуди повністю
характеризує гармонічне коливання.
,
а проекція його кінця зробить одне повне
коливання навколо положення рівноваги
O,
отже, обертовий вектор амплітуди повністю
характеризує гармонічне коливання.
Нехай точка бере участь у двох гармонічних коливаннях однакової частоти, які напрямлені вздовж однієї прямої:
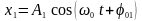 ,
,
 .
.
Ці коливання зручно
додати, користуючись методом обертального
вектора амплітуди. Для цього відкладемо
з точки О
під кутом
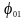 вектор амплітуди
вектор амплітуди
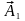 ,
а під кутом
,
а під кутом
 - вектор амплітуди
- вектор амплітуди
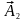 (рис. 29).
(рис. 29).
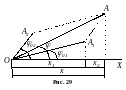
Оскільки вектори
і
обертаються з однаковою кутовою
швидкістю, то різниця фаз
![]() між ними постійна. Оскільки сума проекцій
двох векторів на одну вісь дорівнює
проекції на ту саму вісь вектора, який
є їх сумою, то результуюче коливання
можна подати вектором амплітуди
між ними постійна. Оскільки сума проекцій
двох векторів на одну вісь дорівнює
проекції на ту саму вісь вектора, який
є їх сумою, то результуюче коливання
можна подати вектором амплітуди
![]() ,
що дорівнює сумі векторів
і
:
,
що дорівнює сумі векторів
і
:
![]()
і який обертається
навколо точки
![]() з тією самою кутовою швидкістю
з тією самою кутовою швидкістю
![]() ,
що й вектори
і
.
Результуюче коливання описуються
рівнянням
,
що й вектори
і
.
Результуюче коливання описуються
рівнянням
![]() ,
,
де
![]() – амплітуда результуючого коливання,
а
– амплітуда результуючого коливання,
а
![]() – його початкова фаза.
– його початкова фаза.
Застосовуючи теорему косинусів до одного з трикутників, на які паралелограм розбивається діагоналлю, з рис. 29 видно, що
![]() ,
,
![]() .
.
Амплітуда A результуючого коливання залежить від різниці початкових фаз коливань, що додаються. Можливі значення A лежать в межах
![]() .
.
Розглянемо кілька окремих випадків.
1). ![]() ,
,
![]() .
.
Тоді
![]() і
і
![]() .
.
2). ![]() ,
,
![]() .
.
Тоді
![]() і
і
![]() .
.
Розглянемо аналітичний метод знаходження результуючого коливання в деяких простих випадках:
а) частоти і фази коливань, що додаються, однакові, амплітуди різні:
![]()
![]() .
.
Амплітуда
результуючого коливання
![]() дорівнює сумі амплітуд коливань, що
додаються.
дорівнює сумі амплітуд коливань, що
додаються.
б) частоти і амплітуди однакові, фази відрізняються на :
![]()
![]() .
.
Амплітуда результуючого коливання
![]()
менша суми
амплітуд, що додаються; зокрема, якщо
![]() ,
то
,
то
![]() .
.
Якщо частоти
коливань
![]() і
і
![]() неоднакові, то вектори
і
будуть обертатися з різною швидкістю.
В цьому випадку результуючий вектор
пульсує за величиною і обертається зі
змінною швидкістю. Результуючим рухом
буде в цьому випадку не гармонічне
коливання, а деякий складний коливний
процес.
неоднакові, то вектори
і
будуть обертатися з різною швидкістю.
В цьому випадку результуючий вектор
пульсує за величиною і обертається зі
змінною швидкістю. Результуючим рухом
буде в цьому випадку не гармонічне
коливання, а деякий складний коливний
процес.
Особливий інтерес становить випадок, коли два гармонічні коливання однакового напрямку, що додаються, мало відрізняються за частотою.
Періодичні зміни амплітуди коливання, які виникають при додаванні двох гармонічних коливань одного напрямку з близькими частотами, називаються биттями.
Нехай амплітуди
коливань
![]() ,
,
![]() ,
,
а частоти дорівнюють
,
![]() і
і
![]() <<
.
<<
.
Тоді рівняння
коливань матимуть вигляд:![]() ,
,
![]() .
.
Додаючи ці вирази
і застосовуючи тригонометричну формулу
для суми косинусів, отримуємо:
![]() .
.
Отриманий вираз
є добуток двох коливань. Оскільки
<<
,
то множник
![]() майже не зміниться, коли множник
майже не зміниться, коли множник
![]() здійснює кілька повних коливань. Тому
результуюче коливання
здійснює кілька повних коливань. Тому
результуюче коливання
![]() можна розглядати як гармонічне з частотою
й амплітудою
можна розглядати як гармонічне з частотою
й амплітудою
![]() .
.
Частота зміни
![]() удвоє більша від частоти зміни косинуса
(оскільки береться за модулем). Частота
биття дорівнює різниці частот коливань,
що додаються, тобто
удвоє більша від частоти зміни косинуса
(оскільки береться за модулем). Частота
биття дорівнює різниці частот коливань,
що додаються, тобто
![]() .
Період биття
.
Період биття
![]() .
.
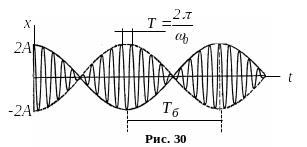
Суцільні лінії
на рис. 30 дають графік результуючого
коливання у випадку
![]() ,
і графік амплітуди
.
,
і графік амплітуди
.
6.Додавання взаємно перпендикулярних коливань.
Нехай матеріальна
точка C
одночасно бере участь у двох гармонічних
коливаннях з однаковою частотою у двох
взаємно
перпендикулярних напрямках як вздовж
осі Х,
так і вздовж осі Y
(рис. 31). Якщо збудити обидва коливання,
матеріальна т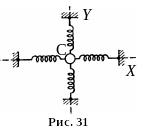 очка
буде рухатись вздовж деякої криволінійної
траєкторії, форма якої залежить від
різниці фаз обох коливань.
очка
буде рухатись вздовж деякої криволінійної
траєкторії, форма якої залежить від
різниці фаз обох коливань.
Виберемо початок відліку часу так, щоб початкова фаза першого коливання дорівнювала нулю. Тоді рівняння коливань матимуть такий вигляд:
![]() ,
,
![]() .
.
де - різниця фаз обох коливань.
Ці вирази –
параметрична форма
рівняння
траєкторії, вздовж якої рухається точка,
що бере участь в обох коливаннях. Щоб
отримати рівняння траєкторії у звичайному
вигляді, треба виключити з цих рівнянь
параметр
![]() .
Проведемо наступні перетворення:
.
Проведемо наступні перетворення:
![]() ,
,
![]() ,
,
![]()
![]()
;
![]() ,
,![]()
![]()
.
В результаті отримаємо
![]() .
.
Це рівняння еліпса, осі якого повернуті відносно координатних осей OX і OY. Орієнтація еліпса і величини його півосей залежать від амплітуд OA і OB і різниці фаз .
Розглянемо частинні випадки.
1).
![]()
![]()
Тоді ![]() ;
;
звідси ![]() .
.
Р езультуюче
коливання є гармонічним вздовж прямої
з частотою
езультуюче
коливання є гармонічним вздовж прямої
з частотою
![]() і амплітудою
і амплітудою
![]() (рис. 32). Пряма утворює з віссю X кут
(рис. 32). Пряма утворює з віссю X кут
![]() .
.
2).
![]() ,
,
![]()
У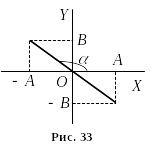 цьому випадку
цьому випадку
![]() ;
;
і
![]() .
.
Результуючий рух – це гармонічне коливання вздовж прямої (рис. 33).
3).
![]()
![]()
В результаті
![]() .
.
Це рівняння еліпса, осі якого збігаються з осями координат, а його півосі дорівнюють відповідним амплітудам (рис. 34).
Якщо А=В, то еліпс вироджується в коло. Випадки
![]() і
і
![]()
відрізняються напрямком руху по еліпсу чи колу.
Якщо частоти взаємно перпендикулярних коливань, що додаються, різні, то замкнена траєкторія результуючого коливання досить складна.
Замкнені траєкторії, що кресляться точкою, яка здійснює одночасно два взаємно перпендикулярні коливання, називаються фігурами Ліссажу. Форма цих кривих залежить від співвідношення амплітуд, частот і різниці фаз коливань, що додаються (рис. 35).