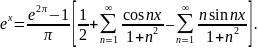Представление непериодической функции рядом Фурье.
1) Пусть у = f (x) непериодическая функция, заданная на всей числовой оси. Такая функция не может быть разложена в ряд Фурье, т. к. сумма ряда Фурье есть функция периодическая и следовательно не может быть равна f(x) для любого х.
Однако непериодическую функцию f (x) можно представить в виде ряда Фурье на любом конечном отрезке [a; b], на котором она удовлетворяет условиям Дирихле. Для этого можно поместить начало координат в середину [a; b] и построить функцию f1 (x) периода Т = 2ℓ, такую, что f1 (x) = f (x) при х∈ [-ℓ; ℓ]. Вне промежутка [-ℓ; ℓ] сумма ряда и f (x) являются совершенно различными функциями.
2) Пусть f (x) – непериодическая функция. Требуется разложить ее в ряд Фурье на [0; ℓ] (Это частный случай п. 1: начало координат перенесено в точку х = а отрезка [a; b]; область определения f (x) будет иметь вид [0; ℓ], где ℓ=b – a|).
Такую функцию можно произвольным образом доопределить на [- ℓ; 0], а потом осуществить ее периодическое продолжение с Т = 2ℓ. Разложив в ряд Фурье на [- ℓ; ℓ] полученную таким образом функцию f1 (x), получим искомый ряд для f (x) при х ∈ [0; ℓ].
В частности, f (x) можно доопределить на [- ℓ; 0] четным образом. В этом случае f (x) разлагается в ряд по косинусам.
Е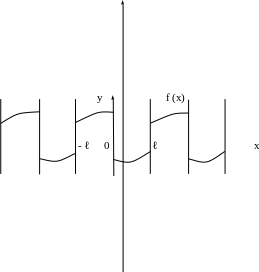
сли
же f
(x)
продолжить на [-
ℓ;
0] нечетным образом, то она разложится
в ряд по синусам.
Ряд косинусов и
ряд синусов для функции f
(x)
заданной на [0; ℓ]
имеет одну и ту же сумму. Если х0
– точка разрыва функции f
(x),
то сумма как одного, так и другого ряда
равна одному и тому же числу
.
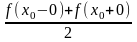Замечание. Все, что было сказано о разложении в ряд Фурье функции f(x) на [0; ℓ] переносится практически без изменения на случай, когда f (x) задана на [0; π].
Примеры решения практических задач
Пример 14.1. Разложить в ряд Фурье функцию
.
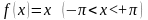Решение. Заданная функция удовлетворяет условиям Дирихле и
может быть разложена
в ряд Фурье. На интервале
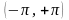функция
– нечетная. Следоватнльно, ряд Фурье
этой функции содержит только синусы
(при косинусах все коэффициенты
,
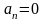n
= 0, 1, 2, 3, …).
Коэффициенты bn определим по формуле
,
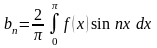в
которую вместо
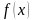надо подставить x.
а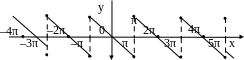
)
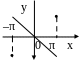б)
в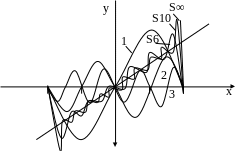
)
Рис.14.1
а) график функции (–π < x < π), б) график функции ( –π < x < π) с ее периодическим продолжением, в) Сумма S6, S10, S∞ шести, десяти гармоник и S∞.
Найдём
⇒
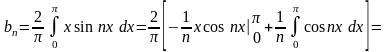
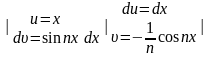
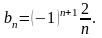
Здесь
учтено, что
.
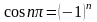Подставим эти значения коэффициентов
в формулу
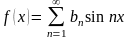
и вынесем постоянный множитель 2 за знак суммы:
.
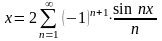Придавая n значения 1, 2, 3, …, получим разложение в развёрнутом виде
.
(*)
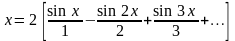В интервале это равенство справедливо в точках непрерывности функций f(x), то есть в данном случае во всех внутренних точках интервала . Вне интервала этот ряд изображает периодическое продолжение рассматриваемой функции.
В
точках разрыва (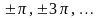
)
сумма ряда равна среднему арифметическому
ее левостороннего и правостороннего
пределов в этих точках.
Найдем эти пределы:
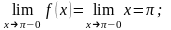
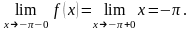
Среднее арифметическое этих пределов
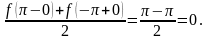
Во всех точках разрыва этой функции получим то же самое.
Таким
образом, в точках разрыва сумма ряда
равна нулю. На рис.14.1(в) к этой задаче
представлены первый, второй и третий
члены ряда, а также – сумма шести, десяти
членов ряда, а также
.
Разложение (*) можно записать так:
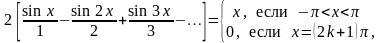
где k – любое целое число.
Если
подставить в разложение (*)
,
которая является точкой непрерывности
заданной функции, получим известную
формулу
.
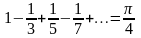Пример 14. 2. Разложить функцию
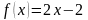
в ряды Фурье из синусов и из косинусов на отрезке [0, 2].
На отрезке [0, 2] данная функция удовлетворяет условиям Дирихле (см. рис. 14.2). Построим графики функций, которые являются нечетным и четным продолжением функции f(x) на отрезок [–2, 0], и затем с отрезка [–2, 2] периодически продолжаем их на всю числовую ось (рис.14.2, рис. 14.3).
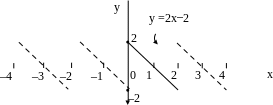
Рис. 14.2
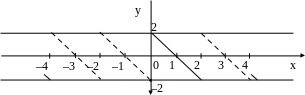
Рис. 14.3
1) Разложение в ряд Фурье из синусов для функции f(x) имеет вид
,
где
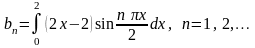
Для вычисления коэффициентов bn применим формулу интегрирования по частям:
.
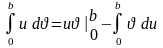Полагая
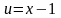(общий множитель 2 вынесем за знак
интеграла),
,
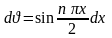находим
,
(
)
.
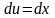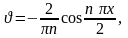
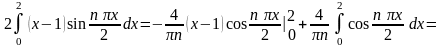
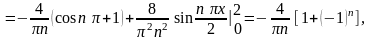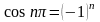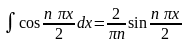Отсюда следует
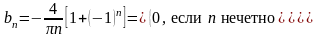
Положив
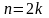(k
= 1, 2…), получаем искомое разложение
функции f(x):
.
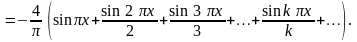
2) Разложение функции f(x) в ряд Фурье из косинусов имеет вид
,
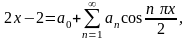где
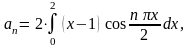
По формуле интегрирования по частям находим
=
;
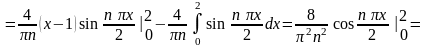
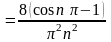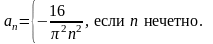
Положив –1 (k = 1, 2,…), получаем разложение данной функции в ряд Фурье из косинусов:
,
.
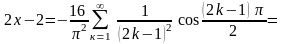
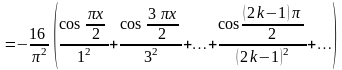ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
14.1. Разложить в ряд Фурье функцию
f(x) = x2 для значений x на отрезке [ ̶ π; + π].
Ответ:
x2=
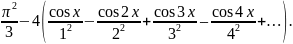
14.2. . Разложить в ряд Фурье функцию
f(x)
=
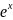для значений x
из интервала [ 0; 2π ].
Ответ:
