Разложение в ряд Фурье 2π – периодических функций.
Будем рассматривать функции f (x), имеющие период Т = 2π.
Теорема Дирихле (достаточное условие разложимости функции в ряд Фурье). Пусть 2π – периодичность f (x) на [- π; π] удовлетворяет условиям:
1) f (x) кусочно-непрерывная, т. е. непрерывна или имеет конечное число точек разрыва первого рода;
2) f (x) кусочно-монотонная, т. е. монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна. Тогда ряд Фурье функции f (x) сходится на [- π; π] и его сумма равна:
1) f (x) во всех точках непрерывности функции f (x), лежащих внутри [-π; π];
2)
во всех точках разрыва;
3)
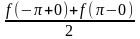на концах промежутка.
Определение. Будем говорить, что функция F (x) определенная на всей числовой прямой и периодическая с Т = 2π является периодическим продолжением функции f (x), если на [- π; π] F (x) = f (x).
Теорема Дирихле справедлива и для периодического продолжения функции f (x).
Ряды Фурье для четных и нечетных функций.
Как известно, если функция f (x) интегрируема на симметричном отрезке [- a; a], то
(*)
Теорема 14.2.(о разложении в ряд Фурье четной функции). Пусть функция f (x) определена на [- π; π] и является четной, т. е. f (x) = f (- x). Тогда ее ряд Фурье имеет вид
,
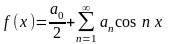(bn=0)
(14.6)
где
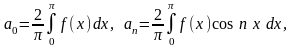(14.7)
Доказательство. Действительно f (x) – четная, следовательно, и f (x)∙cosnx – четная. По формуле(*) а0, аn определяются формулами (14.7) и
Теорема 14.3. (о разложении в ряд Фурье нечетной функции). Пусть функция f(x) нечетная и определена на [- π; π]. Тогда ее ряд Фурье имеет вид
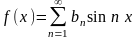(14.8)
где
.
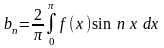(14.9)
Доказательство. Действительно
f (x) – нечетная, f (x)∙sin n x – четная; f (x)∙cos n x – нечетная. Отсюда по формуле (*) вытекает (14.9), а0 = 0, ап = 0.
Ряды, стоящие в правой части формул (14.6) и (14.8) называются неполными тригонометрическими рядами, или рядами из косинусов и синусов соответственно.
Разложение в ряд Фурье функций на отрезке [-ℓ; ℓ].
Теорема 14.4. Пусть f (x) определена на [- ℓ; ℓ] (ℓ – произвольное положительное число) и удовлетворяет на этом отрезке условиям Дирихле, тогда ее разложение в ряд Фурье на [-ℓ; ℓ] имеет вид
(14.10)
,
,
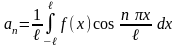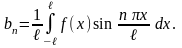(14.11)
Доказательство.
Преобразуем f
(x),
сделав подстановку
,
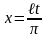в функцию
,
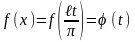которая определена на [-
π;
π]
и имеет периодом 2π.
Кроме того φ (t) удовлетворяет условиям Дирихле. Разложим φ (t) на [- π; π] в ряд Фурье
,
,
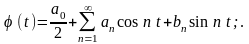
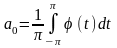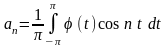Возвращаясь к переменной
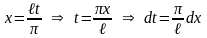
получим (14.10)
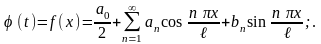
где аi, bi находятся по формулам (14.11).
Замечание. Все теоремы, имеющие место для рядов Фурье 2π – периодических функций остаются в силе и для рядов Фурье 2ℓ – периодических функций.
В частности, если f (x) на [- ℓ; ℓ] четная, то ее ряд Фурье имеет вид
,
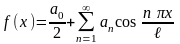где
;
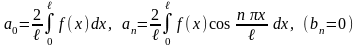если f (x) нечетная, то
.
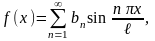
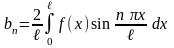