Выпуклые оболочки / diplom

Министерство науки и образования Российской Федерации ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Факультет информатики

Кафедра теоретических основ информатики

УДК 681.03

ДОПУСТИТЬ К ЗАЩИТЕ В ГАК Зав. кафедрой, д.т.н., проф.

__________ Костюк Ю. Л. «___»____________ 2004 г.

Чаднов Роман Витальевич

АЛГОРИТМЫ ПОСТРОЕНИЯ ВЫПУКЛЫХ ОБОЛОЧЕК И ИХ ПРИМЕНЕНИЕ В ГИС И САПР

Дипломная работа

Электронная версия дипломной работы помещена в электронную библиотеку. Файл Администратор

Томск – 2004

Реферат

Дипломная работа 61 с., 49 рис., 17 источников.

ВЫПУКЛЫЕ ОБОЛОЧКИ, ТРИАНГУЛЯЦИЯ ДЕЛОНЕ, ВЫЧИСЛИТЕЛЬНАЯ ГЕОМЕТРИЯ, КОМПЬЮТЕРНАЯ ГРАФИКА, ГЕОИНФОРМАЦИОННЫЕ СИСТЕМЫ, СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ, ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ

Объект исследования – алгоритмы построения выпуклых оболочек на плоскости и в трехмерном пространстве.

Цель работы – анализ и исследование известных алгоритмов построения выпуклых оболочек с целью определения наиболее продуктивных алгоритмов для применения на практике; разработка эффективных алгоритмов построения выпуклых оболочек; исследование возможностей применения алгоритмов построения выпуклых оболочек в трехмерном пространстве для построения триангуляции Делоне.

Метод исследования – экспериментальный.

Результаты работы – описаны широко известные и новые алгоритмы построения выпуклых оболочек в двух- и трехмерном пространствах, исследована их производительность и возможность практического применения. Описан комбинированный алгоритм построения выпуклой оболочки на плоскости, устойчивый к типу распределения исходных данных.

Степень внедрения – разработана библиотека алгоритмов построения выпуклой оболочки на плоскости и в пространстве, которая может быть применена в различных приложениях. В настоящее время разработанная библиотека используется в коммерческой геоинформационной системе IndorGIS 5.0 для построения выпуклых оболочек на плоскости.

Прогноз о развитии исследования – автором планируется продолжение исследования и разработки эффективных алгоритмов вычислительной геометрии. В ближайшее время автор планирует заняться разработкой алгоритмов построения выпуклой оболочки в трехмерном пространстве, а также применением этих алгоритмов для построения триангуляции с ограничениями.

2

3

Введение

Вычислительная геометрия [1,2] занимается изучением разработки и исследования алгоритмов для решения геометрических проблем. Задача построения выпуклых оболочек, является одной из центральных задач вычислительной геометрии. Важность этой задачи происходит не только из-за огромного количества приложений (в распознавании образов, обработке изображений, базах данных, в задаче раскроя и компоновки материалов, математической статистике), но также и из-за полезности выпуклой оболочки как инструмента решения множества задач вычислительной геометрии.

Эта задача позволяет разрешить целый ряд других, иногда с первого взгляда не связанных с ней вопросов: построение диаграмм Вороного, построение триангуляций и т.д. Построение выпуклой оболочки конечного множества точек на плоскости довольно широко исследовано и имеет множество приложений. Очень широко алгоритмы построения выпуклой оболочки используются в геонформатике и геоинформационных системах.

Задача построения выпуклой оболочки имеет давнюю историю. Она является одной из первых задач вычислительной геометрии, с которой начала зарождаться эта наука. В настоящее время известно достаточно большое число алгоритмов построения выпуклой оболочки, однако существует проблема, связанная с недостаточным количеством работ, посвященных анализу и/или обзору этих алгоритмов, особенно в трехмерном пространстве. В данной работе предпринята попытка восполнить этот недостаток.

Вглаве 1 дано формальное описание задачи построения выпуклой оболочки.

Вглаве 2 изложены результаты выполненного автором описания и некоторого анализа наиболее распространенных современных алгоритмов построения выпуклой оболочки, как в двумерном, так и в трехмерном пространствах.

Вглаве 3 описаны предложенные автором модификации нескольких существующих алгоритмов, нацеленные на увеличение скорости их работы.

Вглаве 4 данной работы приведены результаты экспериментального сравнения скорости работы алгоритмов на различных классах входных данных.

Вглаве 5 описаны практические результаты работы – внедрение результатов работы в ГИС и САПР.

4

1 Определения и постановка задачи

1.1 Задача построения выпуклой оболочки

Понятие выпуклой оболочки формально определяется следующим образом [1]:

Определение 1. Выпуклой оболочкой (ВО) множества точек S называется наименьшее выпуклое множество, содержащее S.

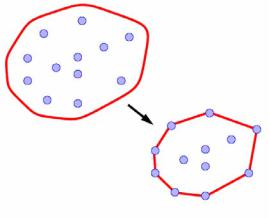
В случае, когда S – конечное множество точек на плоскости, это определение можно представить наглядно. Предположим, что множество точек охвачено большой растянутой резиновой лентой. Эта лента имеет форму выпуклой оболочки. (см. рис. 1.)

Однако приведенное выше простое определение выпуклой оболочки неконструктивно. Для более формального описания необходимо ввести некоторые дополнительные понятия. Будем рассматривать d-мерное евклидово пространство Ed.

Определение 2. Область F, принадлежащая пространству Ed, будем называть выпуклой, если для любой пары точек f1 и f2, принадлежащих F, отрезок f1f2 целиком принадлежит D.

Определение 3. Выпуклой оболочкой множества точек S, принадлежащих пространству Ed, называется граница наименьшей выпуклой области в Ed, которая охватывает S.

Рис. 1. Иллюстрация определения выпуклой оболочки в пространстве Ed

Выпуклая оболочка множества точек S обычно обозначается как CH(S) [1].

Задача построения выпуклой оболочки на плоскости обычно ставится в двух вариантах.

Задача CH1. В Ed задано множество S, содержащее n точек. Требуется определить те из них, которые являются вершинами выпуклой оболочки CH(S).

Задача CH2. В Ed задано множество S, содержащее n точек. Требуется построить их выпуклую оболочку (т.е. найти полное описание границы CH(S)). Ответом этой задачи является упорядоченный список граней выпуклой оболочки.

В двумерном случае гранями являются вершины и ребра оболочки. В трехмерном случае выпуклая оболочка описывается набором граней, ребер, и точек, принадлежащих ей.

Задача CH1 обычно возникает в теории, а на практике она используется редко ввиду низкой практической полезности результатов решения этой задачи.

На рис. 2 проиллюстрирован пример задачи построения выпуклой оболочки на плоскости. Множество S состоит из тринадцати точек. Результатом работы алгоритма построения

5

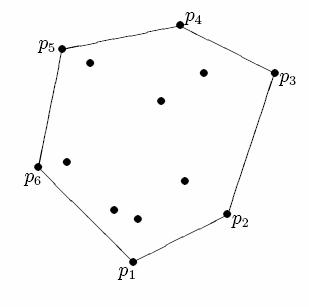
выпуклой оболочки должен быть список (p1, p2, p3, p4, p5, p6). Стоит отметить, что список, содержащий вершины выпуклой оболочки может начинаться с любой из вершин, входящих в неё. К примеру, список (p3, p4, p5, p6, p1, p2) тоже является правильным результатом.

Рис. 2. Тринадцать точек, шесть из которых являются вершинами выпуклой оболочки

Замечание: если pq является ребром выпуклой оболочки множества S, и существует точка r S \{p,q}, которая находится на ребре pq, то считается, что точка r не является вершиной выпуклой оболочки.

1.2 Трудоемкость алгоритмов построения выпуклой оболочки

Сведем задачу сортировки n положительных действительных чисел x1,.., xn к задаче CH2. Поставим в соответствие числу xi точку (xi, xi2) и присвоим ей номер i. Выпуклая оболочка этого множества, представленная в стандартном виде будет представлять собой упорядоченное относительно значения абсциссы множество всех точек из исходного. Из него за линейное время можно получить отсортированный список.

Задача сортировки за линейное время сводится к задаче построения выпуклой оболочки, и, следовательно, трудоемкость нахождения упорядоченной выпуклой оболочки для n точек на плоскости составляет не менее O(n log n).

1.3 Количество граней выпуклой оболочки

Если в пространстве Ed задано множество S, состоящее из n точек, то сколько граней содержит выпуклая оболочка этого множества? Если размерность пространства равна двум, то, очевидно, что количество граней не превысит 2n, т.к. выпуклая оболочка S – это многоугольник, состоящий из не более n вершин и n ребер. Для d = 3, используя формулу Эйлера (V-E+F=2, где V – количество вершин, Е – количество ребер, F – количество граней), можно определить, что количество ребер и граней линейно соотносится с исходным количеством точек, так что общее число граней также имеет порядок O(n). Как показано в [3], для более высоких размерностей, к примеру, для d=4 или d=5 число граней может быть квадратичным,

а для d ≥6 это число имеет порядок O( n d / 2 ).

6

2 Обзор алгоритмов

2.1 Алгоритмы построения выпуклых оболочек в двухмерном пространстве

2.1.1 Алгоритм обхода Джарвиса (Jarvis march)

Этот алгоритм, предложенный Джарвисом в 1973 в [4], очень легок для понимания. Он также известен под названием «метод заворачивания подарка», так как этот алгоритм обрабатывает точки выпуклой оболочки одну за другой, как если бы мы оборачивали множество точек листом бумаги. Джарвис обратил внимание на то, что многоугольник, которым является выпуклая оболочка, с одинаковым успехом можно задать упорядоченным множеством, как его ребер, так и его вершин. Если задано множество точек, то довольно трудно быстро определить, является или нет некоторая точка крайней. Однако если даны две точки, то непосредственно можно проверить, является или нет соединяющий их отрезок ребром выпуклой оболочки.

Алгоритм начинает свою работу с нахождения точки p1 из S, которая гарантированно является вершиной выпуклой оболочки. Обычно за точку p1 берется самая нижняя из точек множества S. Если S содержит несколько точек с минимальной ординатой, то берется самая левая из них. Очевидно, что точка p1 может быть найдена за время O(n).

Так как p1 является вершиной выпуклой оболочки, то обязательно должна существовать такая точка p2, которая также является вершиной выпуклой оболочки, а ребро, соединяющее эту точку с точкой p1p2, является ребром выпуклой оболочки. Таких точек всегда две. Возьмем точку p2 такой, что ребро p1p2 расположено против часовой стрелки.

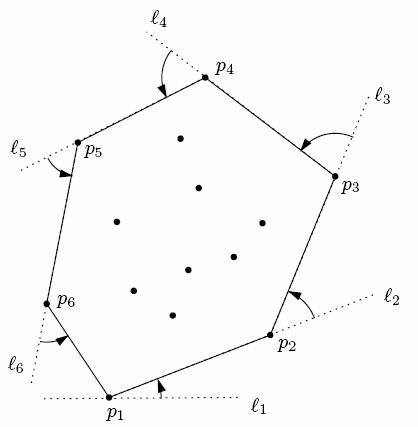
Точка p2 находится следующим образом. Пусть l1 – горизонтальная линия, проходящая через p1. Тогда p2 – первая точка, которой коснется линия l1, если её поворачивать относительно точки p1 против часовой стрелки. Пусть для каждой точки q S \ {p1} определен угол αq – угол между l1 и отрезком p1q. Заметим, что 0 ≤ αq < 2π. Следовательно, p2 – это такая точка из S \ {p1}, для которой этот угол минимален. Если таких точек несколько, то p2 – так из них, которая наиболее удалена от p1.

Таким образом, имея p1, мы можем найти следующую вершину выпуклой оболочки, рассмотрев все точки q S \ {p1}, и выбрав из них ту, для которой угол αq минимален. Это можно сделать за время O(n). Проще говоря, р2 - это точка, имеющая наименьший положительный полярный угол относительно точки p1 как начала координат.

Дальнейший ход алгоритма идет тем же путем. Пусть l2 –линия, проходящая через p1 и p2. Тогда для каждой точки q S \ {p2} определим угол αq – угол между l2 и отрезком p2q. (Теперь αq – это угол, на который мы должны повернуть l2 против часовой стрелки, чтобы коснуться ею точки q). Тогда p3, следующая вершина выпуклой оболочки – это та точка, чей α-угол минимален. Следовательно, p3 можно найти за время O(n).

Мы продолжаем нахождение вершин выпуклой оболочки p4, p5, … до тех пор, пока не вернемся в p1. Алгоритм Джарвиса обходит кругом выпуклую оболочку (отсюда и соответствующее название — обход Джарвиса), порождая в нужном порядке последовательность вершин выпуклой оболочки, по одной на каждом шаге (рис. 3).Более формально, если ph+1 = p1, то мы останавливаемся, и можем вывести выпуклую оболочку (p1, p2, ….. , ph). Ко-

нец алгоритма. ■

Трудоемкость этого алгоритма составляет O(hn), где h – общее количество вершин, входящих в выпуклую оболочку. Первая вершина p1 находится за время O(n). Имея p1, 2, … pk

7

мы находим следующую вершину выпуклой оболочки за время O(n). Таким образом, общее время выполнения алгоритма может быть вычислено как

O ∑h+1 n = O(n (h +1))= O(n h)k =1

Так как h может принять любое значение от 2 до n (все n точек множества могут лежать на его выпуклой оболочке), то трудоемкость алгоритма Джарвиса в худшем случае является квадратичной. Однако если h мало, то этот алгоритм является весьма эффективным.

Рис. 3. Построение выпуклой оболочки методом Джарвиса.

Достоинства:

•Алгоритм Джарвиса может быть применен в пространствах размерности больше двух.

•При априорном знании малости числа вершин оболочки в теории даёт оптимальную трудоемкость.

Недостатки:

•Высокая квадратичная трудоемкость в худшем случае.

8

2.1.2 Алгоритм обхода Грэхема (Graham Scan)

Алгоритм Грэхема называют ([1]) первым алгоритмом вычислительной геометрии. Этот алгоритм был описан в одной из первых работ Грэхема [5], специально посвященной вопросу разработки эффективных геометрических алгоритмов, показал, что, выполнив предварительно сортировку точек, крайние точки можно найти за линейное время. Использованный им метод стал очень мощным средством в области вычислительной геометрии.

Алгоритм начинает свою работу с нахождения начальной точки p1 из S, которая гарантированно является вершиной выпуклой оболочки. За точку p1 берется самая левая из самых нижних точек множества S, также, как и в методе Джарвиса. Очевидно, что точка p1 может быть найдена за время O(n).

Далее все точки исходного множества сортируются по возрастанию полярного угла, образованного каждой текущей точкой q, при условии, что точки, находящиеся точно выше начальной точки, обладают нулевым углом, а полярные углы растут по направлению часовой стрелки.

Рисунок 4. Порядок расположения точек в алгоритме Грэхема

Отсортированные точки следует поместить в двусвязный список (p1, p2, …, pn). Обход Грэхема заключается в сканировании полученного отсортированного списка и удалении из него точек, не входящих в выпуклую оболочку.

Для дальнейшего описания алгоритма введем следующее обозначение: будем говорить, что три точки a, b и c образуют левый поворот, если точка c находится слева от прямой, образованной вектором, направленным из точки a в b.

Это делается путём «метода трех монет». Его суть такова: на каждом шаге проверяется взаимное расположение трех точек (которые «помечены монетами»). Изначально помечаются первые три точки в отсортированном списке. Проверка состоит в определении, образуют ли три проверяемые точки левый или правый поворот. Если точки образуют левый поворот, то средняя из них удаляется из списка, и «монеты» двигаются назад, то есть после удаления некоторой точки pt из тройки pt-1, pt, pt+1, точка pt+1 (вследствие удаления) становится на место pt, а помеченными становятся точки pt-2, pt-1, pt и проверка повторяется. Процесс останавливается, когда первой проверяемой точкой опять становится первая точка множества p1.

Конец алгоритма. ■

Так как за каждый просмотр мы или удаляем одну точку, или переходим к следующей, а просмотр заканчиваем при достижении начальной точки, которая не удалится, то мы выполняем не более n шагов.

Итого общая трудоёмкость алгоритма Грэхема составляет сумму трудоемкости алгоритма сортировки и трудоемкости сканирования

9

О(n log n) + О(n) = О(n log n).

Недостатки:

•Теоретически алгоритм Грэхема является оптимальным в худшем случае, однако он не оптимален в среднем.

•Алгоритм не является открытым, для его работы необходимо априорное знание всего набора точек.

•Неизвестны обобщения алгоритма на пространства размерности больше двух.

Достоинства:

•Алгоритм Грэхема имеет гарантированную линейно-логарифмическую трудоемкость.

2.1.3 Алгоритм монотонных цепочек Эндрю (Monotone Chain)

Алгоритм Эндрю, описанный в 1979 в [6], является модификацией алгоритма Грэхема, которая использует лексикографическое упорядочение точек по координатам. Это является большим преимуществом, так как в этом случае не приходится использовать вещественные числа и тригонометрические операции. Алгоритм Эндрю по отдельности вычисляет верхнюю и нижнюю оболочки из последовательных цепей точек.

Пусть a и b – самая нижняя из самых левых и самая верхняя из самых правых точек исходного множества, соответственно. Очевидно, что a и b являются лексикографически самой большой и самой маленькой точками множества S. Заметим, что a и b также являются вершинами выпуклой оболочки.

Пусьт (p1, p2, …, ph) – вершины выпуклой оболочки множества S, выстроенные таким образом, что p1=a. Пусть r – индекс, такой, что p1=b. Линия, соединяющая a и b, разделяет вы-

пуклую оболочку на две полигональных цепочки (p1, p2, …, pr) и (pr, pr+1, …, ph, p1). Эти це-

почки называются верхней и нижней оболочками (см. Рис 7.).

Рисунок 5. Линия, проходящая через a=p1 и b=p4 делит выпуклую оболочку на верхнюю и нижнюю оболочки.

После такого разбиения для построения выпуклой оболочки S достаточно построить верхнюю и нижнюю оболочки, и после объединить их. Далее будет показано, как строится верхняя оболочка. Нижняя оболочка строится симметричным образом.

10