Выпуклые оболочки / diplom

Первый шаг этого алгоритма имеет трудоемкость O(n log n). Трудоемкость второго шага равна O(∑ik=0 hi ) = O(n) . Таким образом, иерархическое представление какого-либо множества может быть получено за время O(n log n).

Однако даже вышеприведенный алгоритм не годится для применения на практике из-за большого количества используемой памяти. Автором было предложено хранить только число k – количество уровней в иерархическом представлении, а для выполнения экстремальных запросов использовать следующий алгоритм, имитирующий прохождение по слоям иерархического представления:

Шаг 1. Зная k, сравнить углы для точек p0 и p2k . Используя формулу (4), выбрать точку p, сохранить её индекс r.

нию к l, сохраняем в p, а её индекс – в r.

После окончания этого алгоритма в p будет лежать точка, являющаяся ответом на экстремальный запрос к исходному множеству точек.

2.3 Алгоритмы построения выпуклых оболочек в трехмерном пространстве

2.3.1 Алгоритм «грубой силы»

Этот алгоритм является простейшим алгоритмом для построения выпуклой оболочки множества S, состоящего из n точек в трехмерном пространстве.

Смысл алгоритма заключается в проверке каждой тройки точек на образование потенциальной грани выпуклой оболочки путем перебора всех остальных точек и проверки их взаимного расположения.

Проверка осуществляется следующим образом: для каждой тройки точек pi,pj,pk мы перебираем точки q S \ {pi , p j , pk }. Если все точки q находятся по одну сторону от треугольни-

ка abc, то этот треугольник является гранью выпуклой оболочки.

В целях ограничения перебора нам необходимо выбирать точки pi,pj,pk таким образом, чтобы проверять каждую тройку только один раз. Это можно сделать, наложив на точки pi,pj,pk следующие условия: индексы j и k, и проекция пространственного треугольника pi,pj,pk на плоскость xOy должна образовывать левый поворот. Конец алгоритма. ■

Трудоемкость этого алгоритма составляет O(n4).

2.3.2 Алгоритм «заворачивания подарка»

Алгоритм, использующий метод «заворачивания подарка», строит выпуклую оболочку множества S, состоящего из n точек в трехмерном пространстве за время O(nh), где h – это количество граней выпуклой оболочки.

Основная идея этого метода состоит в последовательной генерации граней выпуклой оболочки путем поиска в ширину или в глубину.

Алгоритм состоит из двух стадий: инициализации и серии шагов «заворачивания».

22

Инициализация. Сначала необходимо найти точку p с минимальной z-координатой (Если таких точек несколько, то берется та из них, которая имеет наименьшую абсциссу, а если и таких точек несколько, то та, которая имеет наименьшую ординату). Пусть H – плоскость, проходящая через p и перпендикулярная к оси z, и l – линия на плоскости H, на которой лежит точка p. Далее мы находим точку q, которая образует минимальный угол между H и плоскостью G, которая содержит q и линию l. Пусть m – линия, проходящая через p и q. Заметим, что m принадлежит плоскости G. Завершается стадия инициализации нахождением точки r, которая образует минимальный угол между G и плоскостью F, которая содержит r и линию m. Плоскость F содержит грань выпуклой оболочки множества S, которая образована треугольником T = ∆pqr . Определим стек Q текущих ребер и поместим в него все ребра

треугольника T.

Шаг алгоритма. На каждом шаге «заворачивания» мы извлекаем из стека Q одно из ребер e. Это ребро инцидентно какой-то грани T выпуклой оболочки S. Мы находим треугольник U, отличный от T, такой, что он является гранью выпуклой оболочки. Это делается путем нахождения точки s, которая образует минимальный угол между плоскостью F, содержащей T, и плоскостью E, которая содержит s и e. Если треугольник U, определяемый точкой s и ребром e, ещё не был обнаружен ранее, то мы добавляем два его ребра, отличные от e в стек Q и, естественно, запоминаем треугольник U.

Этот шаг повторяется до тех пор, пока стек Q не станет пустым. Когда это выполнится, в списке сохраненных треугольников мы будем иметь выпуклую оболочку множества S. Конец алгоритма. ■

Так как на каждом шаге мы находим одну точку из исходного множества S, то трудоемкость шага этого алгоритма равна O(n). Учитывая, что h – это количество граней выпуклой оболочки, мы сделаем не более h шагов. Таким образом, трудоемкость алгоритма «заворачивания подарка» равна O(nh). Как и в плоском случае, алгоритм, основанный на этой методике, будет полезен при малых h, так как в случае, когда все точки множества S входят в выпуклую оболочку, этот алгоритм будет иметь квадратичную трудоемкость.

2.3.3 Алгоритм «разделяй и властвуй»

Этот алгоритм, предложенный Препаратой и Хонгом в [12], основан на методике «разделяй и властвуй», и, в отличие от предыдущего, имеет гарантированную линейнологарифмическую трудоемкость в худшем случае.

Алгоритм начинает свою работу с разделения множества S на примерно равные по мощности подмножества S1 и S2, отделяемые друг от друга некоторой плоскостью H, которая перпендикулярна оси, по которой координаты точек множества S имеют наибольший размах.

Далее мы рекурсивно находим выпуклые оболочки множеств S1 и S2 – C1 и C2 соответственно. Затем необходимо найти «мост» между этими двумя многогранник. Сначала мы проецируем C1 и C2 на некоторую плоскость G в направлении r , параллельном H, и находим некоторое ребро e между двумя спроецированными двумерными выпуклыми оболочками. Проецируя точки назад в трехмерное пространство, мы можем увидеть, что ребро e переходит в ребро, (p,q) соединяющее точки p на С1 и q на С2. Более того, плоскость W, содержащая это ребро и вектор r , является касательной к выпуклой оболочке множества S. Дальнейшее вычисление моста заключается в последовательном нахождении треугольников, принадлежащих выпуклой оболочке, состоящих из ребра на одном из многогранников C1 или C2, и точки на другом из них.

Нахождение треугольников, формирующих мост, начинается с уже найденного ребра (p,q). Таким образом, на каждом шаге мы имеем некоторое ребро (p,q) такое, что p находится на С1 и q находится на С2. Проверив вершины С1, инцидентные вершине p, мы можем найти

23

ребро (p,r) на С1, которое образует минимальный угол с плоскостью W. Аналогично, проверив вершины из С2, инцидентные q, мы можем найти ребро (q,s) на С2, которое образует минимальный угол с плоскостью W. Тот из треугольников pqs и prq, который образует минимальный угол с плоскостью W, будет являться следующим треугольником моста. Далее алгоритм продолжает вычисления, начиная с другого ребра полученного треугольника, вершины которого находятся на C1 и C2. Эти вычисления продолжаются до тех пор, пока алгоритм не вернется к первому ребру. Конец алгоритма. ■

Такой алгоритм вычисления моста имеет трудоемкость O(n). Тогда общая трудоемкость алгоритма построения выпуклой оболочки будет равна O(n log n).

2.4 Обзор областей применения

2.4.1 В ГИС и САПР

В ГИС и САПР одно из наиболее серьезных применений средств вычислительной геометрии является задача моделирования различных поверхностей, представляемых в виде триангуляций, в частности триангуляции Делоне [13]. В настоящее время одним из перспективных направлений быстрого вычисления триангуляции Делоне является применение алгоритма построения трехмерной выпуклой оболочки по специально сформированному набору точек в пространстве . В настоящее время разработаны различные программы построения триангуляции Делоне на основе трехмерных выпуклых оболочек, имеющих очень приличное время работы по сравнению с другими известными алгоритмами [14].

Другой пример применения – это диаграмм Вороного и различные виды их обобщения. Диаграммы Вороного очень удобно строить по триангуляции Делоне, которая, в свою очередь, может быть построена с помощью трехмерных выпуклых оболочек.

2.4.2 Другие области

Также алгоритмы построения выпуклых оболочек широко используются во многих областях науки и техники.

Ниже следует перечисление некоторых областей применения алгоритмов построения выпуклых оболочек:

•СУБД. Для выполнения запросов на экстремальность данных по нескольким параметрам.

•Робототехника. Для определения оптимальных путей обхода препятствий

•Материаловедение. В широко используемом методе конечных автоматов.

•Кристаллография. Для облегчения изучения поверхностей кристаллов.

•Компьютерные сети. Выпуклые оболочки используются в алгоритмах маршрутизации.

2.5 Существующие проблемы в области разработки алгоритмов построения выпуклых оболочек

Существует несколько проблем, ограничивающих использование стандартных теоретических алгоритмов построения выпуклой оболочки. Приведем некоторые из них:

1. Стремительный рост объёмов данных. В настоящее время в коммерческих системах, использующих алгоритмы построения выпуклой оболочки, объёмы данных настолько велики, что существующие алгоритмы, которые имеют временную сложность O(n3/2) или O(n log n), не справляются с задачей за приемлемое время. Вследствие этого возникает необ-

24

ходимость разработки алгоритмов с временной сложностью O(n) в среднем или близкой к ней.

2.Вычислительная устойчивость. Существующие алгоритмы построения выпуклой оболочки являются чисто теоретическими, не привязанными к конкретным данным, моделям вычислений и платформам. Вследствие этого в практических реализациях этих алгоритмов имеет место вычислительная неустойчивость, что неизбежно ведет к потерям в качестве работы алгоритмов.

3.Недостаточное количество работ, посвященных анализу и/или обзору алгоритмов построения выпуклой оболочки, особенно на русском языке.

25

3 Модификации алгоритмов

В данной главе описаны некоторые известные и предложенные автором модификации существующих алгоритмов, предназначенные для ускорения скорости их быстродействия.

3.1 Модификации алгоритмов на плоскости

3.1.1 Отсечение восьмиугольником

В качестве предварительной обработки исходного множества точек для отсечения тех точек, которые заведомо не попадут в выпуклую оболочку, было предложено провести отсечение точек, которые попадают в специально построенный восьмиугольник. Похожая методика была применена Эклом в

Алгоритм построения восьмиугольника таков: его вершинами являются точки, имеющие наибольшую x-координату; наибольшую сумму координат; наибольшую y-координату; наименьшую разность координат x и y; наименьшую x-координату; наименьшую сумму координат; наименьшую y-координату; наибольшую разность координат x и y соответственно. Восьмиугольник представляется в виде множества точек f0, f1,…, f8, причем точки с индексами от 0 до 7 определяются в вышеприведенном порядке, а точка f8 принимается равной точке f0.

Рисунок 14. Формирование восьмиугольника

Далее для каждой точки pi S проводится проверка попадания в восьмиугольник. Для каждого j=0..7 если точки pi,fj,fj+1 образуют левый поворот, то точка pi выбрасывается из дальнейшего рассмотрения алгоритмом построения выпуклой оболочки.

Однако данный метод предобработки исходного множества точек имеет свои недостатки: восьмикратная проверка всех точек с вычислением на каждом шаге ориентированной площади треугольника может занять слишком большое время.

Трудоемкость данного метода отсечения составляет, очевидно, O(n).

26

Всилу того факта, что множество точек, оставшихся после отсечения, сильно растянуто

ккраям, автором рекомендуется использовать для окончательного построения выпуклой оболочки метод Грэхема, который имеет высокое быстродействие на таких распределениях входных данных.

Рисунок 15. В результате отсечения из двадцати точек останутся только девять.

3.1.2 Отсечение прямоугольником

Метод отсечения прямоугольником является гораздо более эффективным, чем предыдущий метод, потому что он избавлен от необходимости вычисления площадей.

Суть метода отсечения прямоугольником состоит в следующем. Сначала находятся четыре точки, на основании которых будет построен прямоугольник. Этими точками являются точки, обладающие следующими свойствами:

•Точка p1 - имеющая наибольшую сумму координат x и y;

•Точка p2 - имеющая наименьшую разность координат x и y;

•Точка p3 - имеющая наименьшую сумму координат x и y;

•Точка p4 - имеющая наибольшую разность координат x и y.

27

Несмотря на приемлемую теоретическую трудоемкость, алгоритм Чена делает слишком много излишних действий, которые, несомненно, уменьшают его быстродействие:

•Каждый шаг подбора значения h включает в себя построение выпуклых оболочек частей исходного множества точек. Однако результаты этого построения учитываются однобоко – только для построения текущего участка выпуклой оболочки. При этом

валгоритме не предусмотрено какого-либо влияния результатов одного шага на другой.

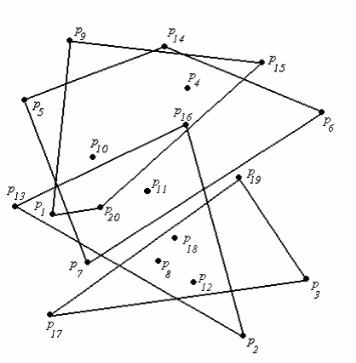
Сточки зрения автора, весьма целесообразным было бы использовать результаты построения выпуклых оболочек частей исходного множества для отсечения точек, которые заведомо не попадут в выпуклую оболочку множества в целом. Очевидно, что точки, отброшенные во время построения выпуклой оболочки какой-либо части исходного множества, должны быть отброшены и из точек – потенциальных вершин выпуклой оболочки всего множества. Рассмотрим рис. 18. Мы можем отбросить точ-

ки p1, p4, p8, p10, p11, p12, p18.

Рисунок 18. Отсечения в алгоритме Чена

Использование этого отсечения позволит улучшить скорость работы алгоритма Чена.

•После построения части выпуклой оболочки, если H оказалось меньше реального h, то алгоритм Чена увеличивает H и начинает построение оболочки снова.

Если же сохранять часть оболочки, полученную на предыдущих шагах, то можно увеличить скорость работы алгоритма.

Алгоритм Чена, использующий приведенные улучшения: первоначальное отсечение точек прямоугольником, отсечение точек на каждом шаге работы алгоритма, а также сохранение уже построенных граней выпуклой оболочки, автором был назван модифицированным алгоритмом Чена.

29