
Задание №5
Регрессия общего вида.
По экспериментальным данным построить
регрессию общего вида, используя
аппроксимирующую функцию F(x)
= k1*1(x)
+ k2*2(x)
+ … + km*m(x),
где
![]() и 1(x)
=
и 1(x)
=
![]() ;
2(x)
=
;
2(x)
=
![]() ;
3(x)
= 1.
;
3(x)
= 1.
Пример: Пусть есть экспериментальные данные
x |
f |
2 |
7 |
3 |
3.2 |
5 |
1.3 |
8 |
-0.9 |
11 |
0.9 |
14 |
1.1 |
17 |
2.2 |
19 |
2.2 |
23 |
3 |
Найдем аппроксимацию, используя метод наименьших квадратов.
Попытаемся найти F(x) в виде: k1*1(x) + k2*2(x) + k3.
Построив точечный график набора пар данных, предположим, искать 1,2(x) в виде 1(x) = ; 2(x) = ,
где a и b некоторые константы, которые попытаемся оптимизировать в поиске решения.
1) Лист Excel оформим следующим образом:
2 |
7 |
|
F= |
15.48120196 |
3 |
3.2 |
|
|
0.0025 |
5 |
1.3 |
|
|
5.364580513 |
8 |
-0.9 |
|
|
25.11123457 |
11 |
0.9 |
|
|
13.3037817 |
14 |
1.1 |
|
|
14.74291222 |
17 |
2.2 |
|
|
9.598819958 |
19 |
2.2 |
|
|
11.0365873 |
23 |
3 |
|
|
8.647399793 |
|
|
|
|
|
|
|
|
|
|
k1 |
1 |
|
Невязка = |
103.289018 |
k2 |
1 |
|
|
|
k3 |
1 |
|
|
|
a |
1 |
|
|
|
b |
1 |
|
|
|
Формула функции F на примере ячейки:
E1 =($B$12/($B$15*A2+1)+$B$13*КОРЕНЬ(A2+$B$16)+$B$14-B2)^2
Невязка равна сумме всех значений F на данных (xi;yi).
Чтобы аппроксимировать заданный точками участок кривой необходимо в ячейки В12-В16 ввести любые начальные значения для их оптимизации.
Теперь входим в поиск решения и устанавливаем:
1.Установить целевую ячейку |
2.Е12 |
||
Равной |
по максимуму |
по минимуму |
по значению |
|
× |
|
|
3.Изменяя ячейки |
4.В12:В16 |
||
5.Ограничения |
|||
Ограничений нет |
|||
Результат:
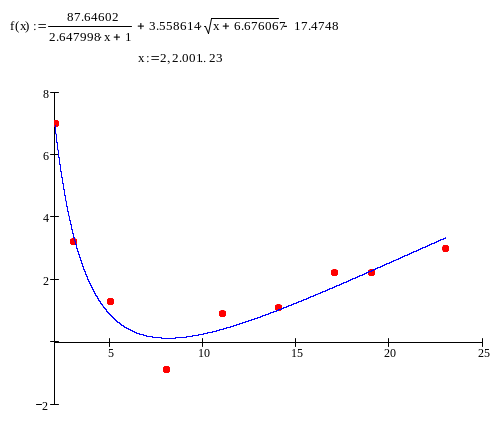
Вариант №1
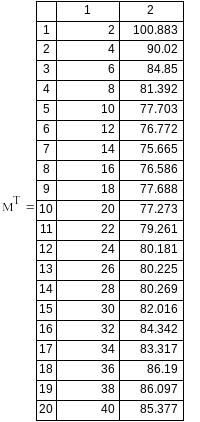
Вариант №2
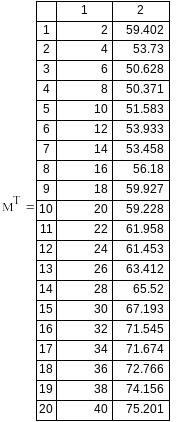
Вариант №3
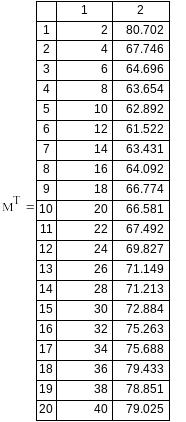
Вариант №4
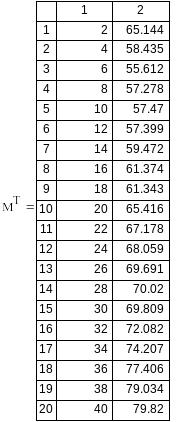
Вариант №5
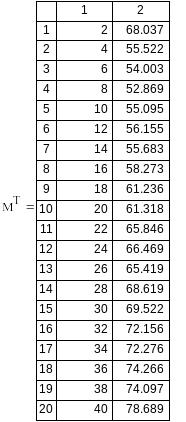
Вариант №6
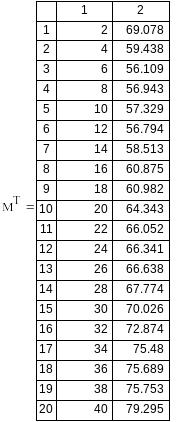
Вариант №7
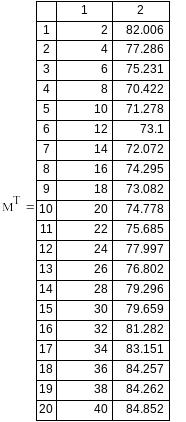
Вариант №8
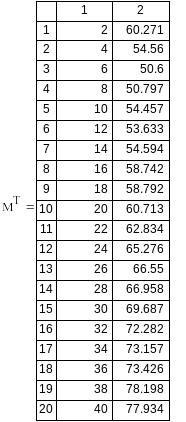
Вариант №9
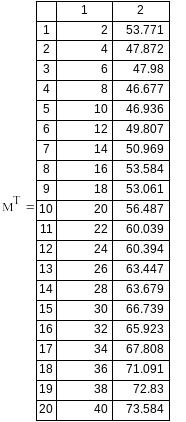
Вариант №10
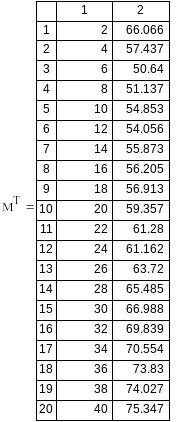
Вариант №11

Вариант №12
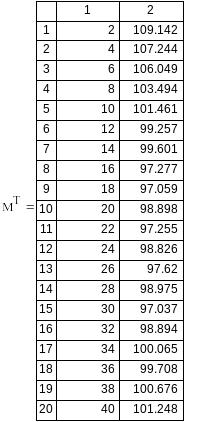
Вариант №13
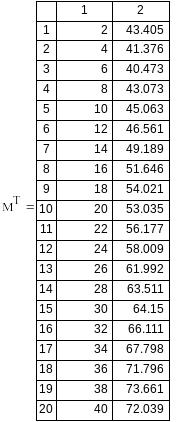
Вариант №14
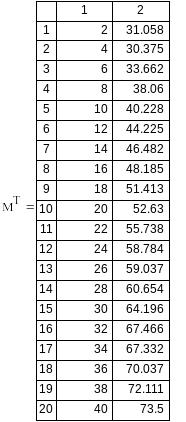
Вариант №15
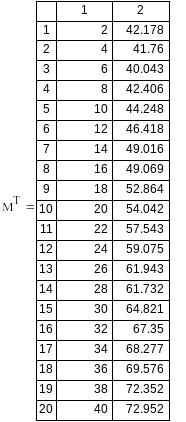
Отчет должен содержать:
название и цель работы;
задания на лабораторную работу;
исходные данные;
описание метода решения задачи;
описание пошагового выполнения расчета в Excel;
проверка полученных результатов;
сопроводительные иллюстрации;
выводы по результатам выполнения лабораторной работы.
