Пример оформления контрольной работы

(Задания данного примера вымышлены и не являются заданиями какого-либо из предлагаемых вариантов)

Псковский государственный политехнический институт

факультет Информатики

Контрольная работа

по дискретной математике

студента группы 682-0902

Иванова Ивана Ивановича

(№ зачетной книжки 0308033)

Вариант № 13

Преподаватель:

Петров Петр Петрович

Псков

2009

Задание 1

Даны множества: Определить множества:

A = {1, 2, 3, 4, 5, 6, 7, 8}; D₁ = B \ (A  C);

B = {2, 4, 6, 8, 10, 12, 14, 16}; D₂ = (A  B)  C;

C = {1, 3, 5, 7, 9, 11, 13, 15}. D = D₁  D₂.

A  C = {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 15}

D₁ = B \ (A  C) = {10, 12, 14, 16}

A  B = {1, 3, 5, 7, 10, 12, 14, 16}

D₂ = (A  B)  C = {1, 3, 5, 7}

D = D₁  D₂ = {(10, 1), (10, 3), (10, 5), (10, 7), (12, 1), (12, 3), (12, 5), (12, 7), (14, 1), (14, 3), (14, 5), (14, 7), (16, 1), (16, 3), (16, 5), (16, 7)}

Задание 2

A = {1, 2, 3, 4, 5, 6, 7, 8};

B = {2, 4, 6, 8, 10, 12, 14, 16}.

Задать списком:

а) отношение R  B  A = {(b, a)  b является делителем a};

б) обратное отношение R^–1;

в) композицию отношений R  R^–1;

г) проекцию множества векторов на вторую ось Пр₂(R  R^–1).

а) R = {(2, 2), (2, 4), (2, 6), (2, 8), (4, 4), (4, 8), (6, 6), (8, 8)}

б) R^–1 = {(2, 2), (4, 2), (6, 2), (8, 2), (4, 4), (8, 4), (6, 6), (8, 8)}

в) R  R^–1 = {(2, 2), (2, 4), (2, 6), (2, 8), (4, 2), (4, 4), (4, 8), (6, 2), (6, 6), (8, 2), (8, 4), (8, 8)}

г) Пр₂(R  R^–1) = {2, 4, 6, 8}

Задание 3

R = {(7, 8), (1, 3), (2, 8), (8, 3)}.

Найти:

а) OO_R (область определения соответствия R);

б) ОЗ_R (область значений соответствия R);

в) образ элемента 8;

г) прообраз элемента 8;

д) является ли соответствие R инъективным? почему?

а) OO_R = {7, 1, 2, 8}

б) ОЗ_R = {8, 3}

в) образ элемента 8 = {3}

г) прообраз элемента 8 = {7, 2}

д) соответствие R не является инъективным, так как не соблюдается условие единственности прообраза. Например, у элемента 3 существует два прообраза: 1 и 8

Задание 4

Н арисовать сильно связный орграф с пятью вершинами, имеющий минимальное количество дуг.

В сильно связном орграфе должен существовать путь из любой вершины в любую другую вершину. Минимальным по количеству дуг будет контур, проходящий по всем вершинам. Покажем существование пути из каждой вершины в каждую. Путь из v₁ в v₂: v₁, v₂. Путь из v₂ в v₁: v₂, v₃, v₄, v₅, v₁. Аналогично можно указать пути и между любыми другими парами вершин. Существует ли сильно связный орграф с пятью вершинами и меньшим количеством дуг, чем 5? Если дуг будет 4, то в лучшем случае, если граф останется связным, мы получим ордерево, в котором только из корня есть путь ко всем остальным вершинам.

Задание 5

Нарисовать граф по следующей матрице. Обозначить вершины (узлы) и/или ребра (дуги) метками v₁, v₂, … и е₁, е₂, … согласно данной матрице.

	1	2	3	4
1	1	1	0	0
2	1	0	1	0
3	0	1	0	1
4	0	0	1	0

В данном случае представленная матрица может быть как матрицей смежности неориентированного графа G₁ (матрица квадратная, симметрична относительно главной диагонали), так и матрицей инцидентности неориентированного графа G₂ (в каждом столбце матрицы не более двух единиц, но при этом нет отрицательных значений).

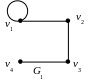
Задание 6

П о следующему графу приведите пример цепи, не являющейся простой (в виде соответствующей последовательности вершин).

b, d, c, g, d, e – данный маршрут является цепью, так как не проходит по одним и тем же ребрам дважды, но не является простой цепью, потому что вершина d встречается в нем более одного раза.

Задание 7

Доказать справедливость соотношения

((a  (c  b))  (b  (a  d))  (d  (b  c))  (a  c))  a = 1

((a  (c  b))  (b  (a  d))  (d  (b  c))  (a  c))  a = 

= ((a + (c  b))  (b + ad)  (d + (b  c))  (a c + ac))  a =

= ((a + (c  b))  (d + (b  c))  (b + ad)  (a c + ac))  a =

= ((a d + (c  b))  (ab c +abc + a cd))  a =

= ((a d + b c +bc)  (ab c +abc + a cd))  a =

= (ab c d + ab c + ab cd)  a = ab c  (d + 1 + d)  a =

= (ab c  1)  a = ab c  a =   =a +b + c + a = 1 +b + c = 1

Задание 8

Найти МДНФ следующей функции без использования карты Карно:

x	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
y	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
z	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
t	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
f	1	–	–	–	0	1	0	0	1	0	–	–	1	–	–	1

= 0000 + 0001 + 0010 + 0011 + 0101 + 1000 + 1010 +

+ 1011 + 1100 + 1101 + 1110 + 1111

0 группа: 0000 *

1: 0001 * 0010 * 1000 *

2: 0011 * 0101 * 1010 * 1100 *

3: 1011 * 1101 * 1110 *

4: 1111 *

0 группа: 000- * 00-0 * -000 *

1: 00-1 * 001- * 0-01 -010 * 10-0 * 1-00 *

2: -011 * 101- * -101 110- * 1-10 * 11-0 *

3: 1-11 * 11-1 * 111- *

0 группа: 00-- 00-- -0-0 -0-0

1: -01- -01- 1--0 1--0 0-01

2: 1-1- 11-- 1-1- 11-- -101

	0000	0101	1000	1100	1111
00--	
-0-0			
-01-
1--0				
0-01		
1-1-					
11--					
-101		

= -0-0 + 11-- + 0-01 =

Задание 9

Определить следующие свойства логической функции, заданной таблицей

x1	0	0	0	0	1	1	1	1
x2	0	0	1	1	0	0	1	1
x3	0	1	0	1	0	1	0	1
f	0	1	0	1	0	1	0	1

1. Является ли f существенно зависящей от аргумента x₁?

2. Является ли f существенно зависящей от аргумента x₂?

3. Является ли f существенно зависящей от аргумента x₃?

4. Является ли f сохраняющей ноль?

5. Является ли f сохраняющей единицу?

6. Является ли f самодвойственной?

7. Является ли f монотонной?

8. Является ли f линейной?

Все положения ответа должны быть обоснованы.

f(0, 0, 0) = f(1, 0, 0)

f(0, 0, 1) = f(1, 0, 1)

f(0, 1, 0) = f(1, 1, 0)

f(0, 1, 1) = f(1, 1, 1)  f не зависит существенно от x₁

f(0, 0, 0) = f(0, 1, 0)

f(0, 0, 1) = f(0, 1, 1)

f(1, 0, 0) = f(1, 1, 0)

f(1, 0, 1) = f(1, 1, 1)  f не зависит существенно от x₂

f(0, 0, 0)  f(0, 0, 1)  f существенно зависит от x₃

f(0, 0, 0) = 0  f сохраняет ноль

f(1, 1, 1) = 1  f сохраняет единицу

f(0, 0, 0)  f(1, 1, 1)

f(0, 0, 1)  f(1, 1, 0)

f(0, 1, 0)  f(1, 0, 1)

f(0, 1, 1)  f(1, 0, 0)  f самодвойственна

f(1, 1, 1) > f(0, 0, 0)

f(1, 1, 0) = f(1, 0, 0)

f(1, 1, 0) = f(0, 1, 0)

f(1, 0, 1) > f(1, 0, 0)

f(1, 0, 1) = f(0, 0, 1)

f(0, 1, 1) > f(0, 1, 0)

f(0, 1, 1) = f(0, 0, 1)  f монотонна

Из таблицы значений функции f понятно, что f = x₃. Эта запись одновременно является и полиномом Жегалкина для функции f. Данный полином – линейный (так как в нем нет слагаемых, являющихся конъюнкциями нескольких переменных), следовательно, и функция f является линейной.