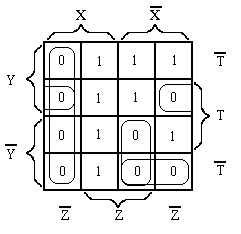
8.4. Нахождение мкнф с помощью карты Карно

Алгоритм поиска МКНФ с использованием карт Карно:

1. Составить карту Карно.

2. Обвести контурами нулевые ячейки.

3. При записи МКНФ переменные, образующие контур, инвертируются, объединяются в дизъюнкции, а затем – в конъюнкции.

Пример. Найти МКНФ функции, заданной таблицей, с помощью карты Карно.

x	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
y	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
z	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
t	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
f	0	1	0	0	1	0	1	1	0	0	1	1	0	0	1	1

8.5. Минимизация логических функций, представленных в конъюнктивной форме, с использованием правил, аналогичных правилам минимизации логических функций в дизъюнктивной форме

КНФ КСНФ СокКНФ ТКНФ МКНФ

a) При табличном задании записать функцию в виде конъюнкции конституент нуля, соответствующих наборам, на которых функция равна нулю. Если функция задана произвольной КНФ, то применить формулы развертывания:

b) Выполнить все возможные операции неполного склеивания и поглощения:

c) и d) Построить матрицу, столбцы которой образуют конституенты нуля КСНФ, а строки – члены СокКНФ. В МКНФ должно входить минимальное число строк, перекрывающих все столбцы.

Пример. Функция задана таблицей

x	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
y	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
z	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
t	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
f	0	1	0	0	1	0	1	1	0	0	1	1	0	0	1	1

1 - 2 * 2 - 3 * 3 - 4 4 - 5

1 - 3 2 - 4 3 - 5 4 - 6

1 - 4 2 - 5 3 – 6 4 - 7

1 - 5 * 2 - 6 3 – 7 4 - 8 *

1 - 6 2 - 7 3 - 8

1 - 7 2 - 8

1 - 8

5 - 6 * 6 - 7 7 - 8 *

5 - 7* 6 - 8*

5 - 8

1 - 2 2 - 3 3 - 4 4 - 5 5 - 6 6 - 7 * 7 - 8

1 - 3 2 - 4 3 - 5 4 - 6 5 - 7 6 - 8

1 - 4 2 - 5 3 - 6 4 - 7 5 - 8 *

1 - 5 2 - 6 3 - 7 4 - 8

1 - 6 2 - 7 3 - 8

1 - 7 2 - 8

1 - 8

								
		
					
			
							