2.1.6. Построение статистических оценок плотности распределения

Статистическими оценками плотности распределения являются полигон частот и гистограмма.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат интервалы (разряды) статистического ряда длиною , а высота равна отношению (плотность относительной частоты). Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

Учитывая свойство плотности распределения можно записать:

P(x^j-1 X<x^j )= f( _j)*l_j , (j= ) , где l_j – длина j-го интервала, f( _j) – средняя на интервале плотность распределения f(x).

Заменяя P(x^j X<x^j+1 ) относительной частотой p^*_j статистического ряда, получим следующее выражение для приближенного значения f^*_j плотности распределения на интервале (разряде):

f^*_j= p^*_j/ l_j , j= .

Таким образом, гистограмма относительных частот строится следующим образом: на оси Оx отложим границы разрядов и на них, как на основаниях, построим прямоугольники, имеющие площадь p^*_j и высоту равную f^*_j (см. рис.3.).

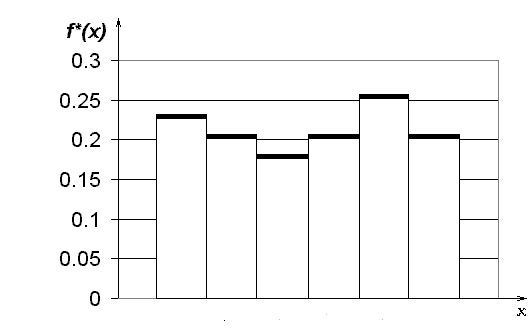
Рис.3. Оценка плотности распределения, построенная по относительным частотам

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат интервалы длиною , а высота равна отношению (см. рис.4.).

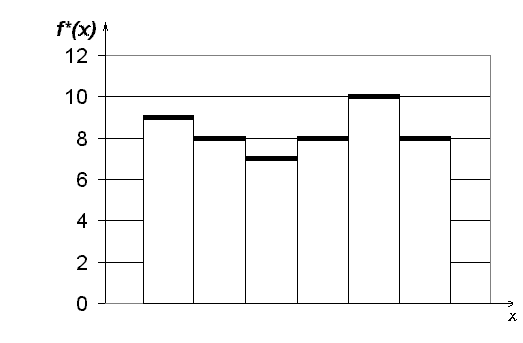
Рис.4. Оценка плотности распределения, построенная по частотам n_j

Сглаженную гистограмму относительных частот в виде ломаной линии называют полигоном относительных частот, являющимся вторым способом оценки f(x). Она строится по точкам ( , ) , j= (см. рис. 5).

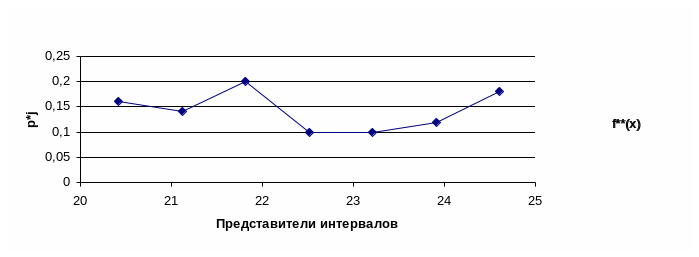
Рис.5. Полигон относительных частот

Полигон частот строим по точкам, координаты которых равны ( , n_j) , j= (см. рис.6).

Рис.6. Полигон частот

2.2. Проверка статистических гипотез о законе распределения случайной величины по критериям согласия

2.2.1. Критерий согласия χ 2 Пирсона

Критерием согласия χ ² Пирсона называют критерий проверки гипотезы о предполагаемой плотности распределения f(x).

Пусть имеется выборка измерений xⁿ=(x₁,…,x_n) и требуется проверить гипотезу Н_о, состоящую в том, что непрерывная случайная величина Х имеет закон нормальный распределения (закон Гаусса). В данном случае в качестве гипотезы выступает параметрический закон распределения с плотностью распределения f(x/ ).

Гипотезу Н_о формируют в виде Х є f(x/ ), где – точечная оценка параметра (найденная по методу максимального правдоподобия).

Тогда алгоритм проверки состоит в следующем:

1. Формулируем гипотезу Н_о: случайная величина имеет закон распределения f₀(x, ₁,…, _r) с r неизвестными параметрами ₁,…, _r .

2. По выборке измерений методом максимального правдоподобия находим точечные оценки неизвестных параметров ₁,…, _r. (например, необходимо найти точечные оценки двух параметров нормального закона m и σ²).

3. Разбиваем выборку на q интервалов, находим их границы х^j ( j= ) и частоты 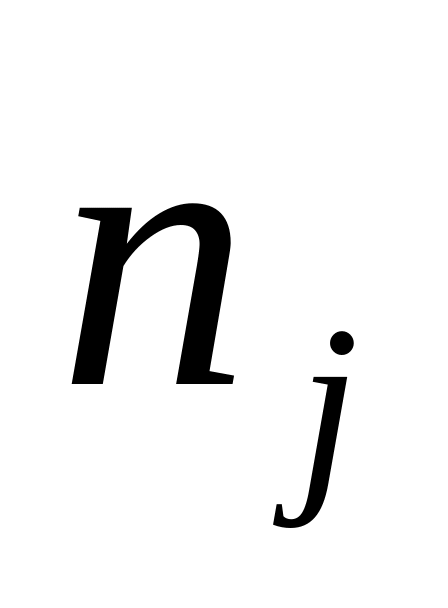(используем данные статистического ряда).

4. Вычисляем вероятность попадания случайной величины в j-ый интервал по формуле:

, j= .

5. Вычисляется наблюдаемое значение критерия:

.

6. Используя таблицу критических точек распределения χ² (Приложение 7), по заданному уровню значимости α и числу степеней свободы k=q-r-1, где q – число интервалов (разрядов), а r – число параметров предполагаемого закона, находят критическую точку χ²_кр(α; k).

Если ( <χ²_кр), гипотеза Н₀ принимается;

Если ( χ²_кр), гипотеза Н₀ отклоняется.

Показано, что точность выводов повышается, если разряды выбирают с соблюдением условия: каждый разряд содержит не менее пяти реализаций х_i.