
- •Введение
- •Задание на расчетно-графическую работу
- •Содержание
- •1. Получение выборки измерений случайной величины 8
- •2. Краткие теоретические сведения 10
- •2.1. Описание первичной статистической обработки результатов измерений случайной величины 10
- •1. Получение выборки измерений случайной величины
- •2. Краткие теоретические сведения
- •2.1. Описание первичной статистической обработки результатов измерений случайной величины
- •2.1.1. Математическое моделирование результатов измерений случайной величины. Выборка измерений
- •2.1.2. Построение вариационного ряда
- •2.1.3. Исключение грубых ошибок измерений
- •2.1.4. Построение статистических оценок математического ожидания и дисперсии
- •Построение точечных оценок
- •Построение интервальных оценок
- •2.1.5. Построение статистического ряда
- •2.1.5. Построение статистических оценок функции распределения Статистическая оценка функции распределения
- •2.1.6. Построение статистических оценок плотности распределения
- •2.2. Проверка статистических гипотез о законе распределения случайной величины по критериям согласия
- •2.2.1. Критерий согласия χ 2 Пирсона
- •2.2.2. Критерий согласия Колмогорова
- •3. Требования к оформлению пояснительной записки к расчетно-графической работе
- •4. Пример выполнения расчетно-графической работы
- •4.1. Исходные данные к расчетно-графической работе
- •4.1.1. Получение выборки измерений
- •4.2. Выполнение расчетно-графической работы
- •4.2.1. Первичная обработка результатов измерений
- •4.2.1.1. Построение вариационного ряда
- •4.2.1.2. Исключение грубых ошибок измерений
- •4.2.1.3. Построение статистических оценок математического ожидания и дисперсии Точечные оценки
- •Интервальные оценки
- •4.2.1.4. Построение статистического ряда
- •Статистический ряд
- •4.2.1.5. Построение статистических оценок функции распределения
- •1. Статистическая функция распределения
- •2. Кумулятивная ломаная
- •4.2.1.6. Статистические оценки плотности распределения
- •Гистограмма
- •Полигон частот
- •4.2.2. Проверка статистических гипотез о законе распределения св
- •4.2.2.1. Критерий согласия χ2 Пирсона
- •4.2.2.2. Критерий согласия Колмогорова
- •Список литературы
- •Приложения
- •Приложение 2. Интервальная таблица
- •Приложение 4. Критерий Колмогорова
- •Приложение 5. Критерий Пирсона
- •Приложение 7. Критические точки распределения Хи–квадрат
- •Приложение 8. Критические точки распределения Колмогорова
- •Министерство образования и науки Российской Федерации Государственное образовательное учреждение
- •Казань 2010
2.1.3. Исключение грубых ошибок измерений
Грубая ошибка измерения – это результат измерения, не соответствующий закону распределения СВ.
В процессе измерений предполагаемая статистическая обстановка может нарушиться, поэтому среди реализаций x1,…,xn могут появиться ошибочные значения, которые не соответствуют закону распределения СВ. Обычно в качестве грубых ошибок подразумевают xmin и xmax.
Для исключения грубых ошибок используют, в частности, приближенный (логический) и точный счетный метод.
По приближенному методу грубые ошибки измерения исключаются по признаку наибольшего отличия проверяемого результата измерения от других результатов измерений.
В соответствии с приближенным методом для выявления грубых ошибок вычисляется расстояние l=x(n-1)-x(2). Затем сравнивается расстояние между последним (максимальным) элементом и предпоследним x(n-1) с вычисленным расстоянием l:
если (x(n) - x(n-1)) < l, то x(n) – не является грубой ошибкой,
если
(x(n)
-
x(n-1))
![]() l,
то x(n)
–
грубая ошибка, которая исключается из
выборки.
l,
то x(n)
–
грубая ошибка, которая исключается из
выборки.
Аналогично проводится проверка на грубую ошибку первого (минимального) элемента вариационного ряда:
если (x(2) - x(1)) < l, то x(1) – не является грубой ошибкой,
если (x(2) - x(1)) l, то x(1) – грубая ошибка, которая исключается из выборки.
При
определении грубых ошибок точным счетным
методом вводится случайная величина
 – статистика проверки статистической
гипотезы о том, что реализация Xmax
является грубой ошибкой. Здесь
– статистика проверки статистической
гипотезы о том, что реализация Xmax
является грубой ошибкой. Здесь
![]() – среднее значение независимых случайных
величин:
– среднее значение независимых случайных
величин:
![]() ,
S
–
точечная оценка стандартного отклонения:
,
S
–
точечная оценка стандартного отклонения:
 .
.
Реализация
статистики T
имеет
вид:
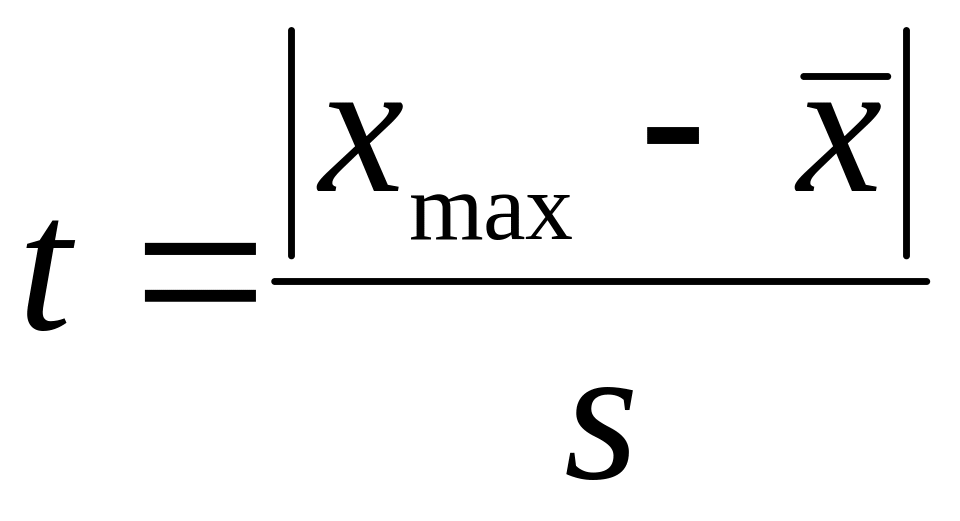 ,
где
,
где
![]() ,
,
 .
.
Для проверки гипотезы о грубой ошибке задается α – уровень значимости, определяющий вероятность практически невозможного события
P(t ta)= α,
состоящего в том, что t – реализация статистики превысит критическое значение ta .
Значение величины ta определяется по таблице приложения 10 по объему выборки n и уровню значимости α. Например, для объема выборки n = 50 и уровня значимости α = 0,05, значение ta=2,987.
Затем
вычисляются значения величин x*min
=
![]() -
sta
и
x*max
=
+
sta.
Если xmin
-
sta
и
x*max
=
+
sta.
Если xmin
![]() x*min
,
или xmax
x*max
то
xmin
и
xmax
не являются грубыми ошибками. В
противоположном случае они являются
грубыми ошибками и исключаются из
выборки.
x*min
,
или xmax
x*max
то
xmin
и
xmax
не являются грубыми ошибками. В
противоположном случае они являются
грубыми ошибками и исключаются из
выборки.
2.1.4. Построение статистических оценок математического ожидания и дисперсии
Статистические оценки математического ожидания и дисперсии разделяют на точечные и интервальные (доверительные).
Построение точечных оценок
Математическим
ожиданием
M[X]
дискретной случайной величины X
называется сумма произведений всех
возможных значений случайной величины
![]() на вероятности
на вероятности
![]() этих значений:
этих значений:
M[X]
=
![]()
Дисперсией случайной величины называется математическое ожидание квадрата соответствующей центрированной случайной величины:
D[X]
= M[(X-
M[X])![]() ]
=
]
=
![]() p
p![]() .
.
Статистической оценкой а* неизвестного параметра а теоретического распределения называют функцию от случайной выборки g(X1, X2, …, Xn).
Точечной оценкой неизвестного параметра а называют статистическую оценку, реализация которой определяется одним числом a*= g(x1, x2, …, xn), где x1, x2, …, xn – выборка измерений, т.е. результаты n измерений случайной величины Х.
Реализация точечной оценки математического ожидания СВ определяется по формуле:
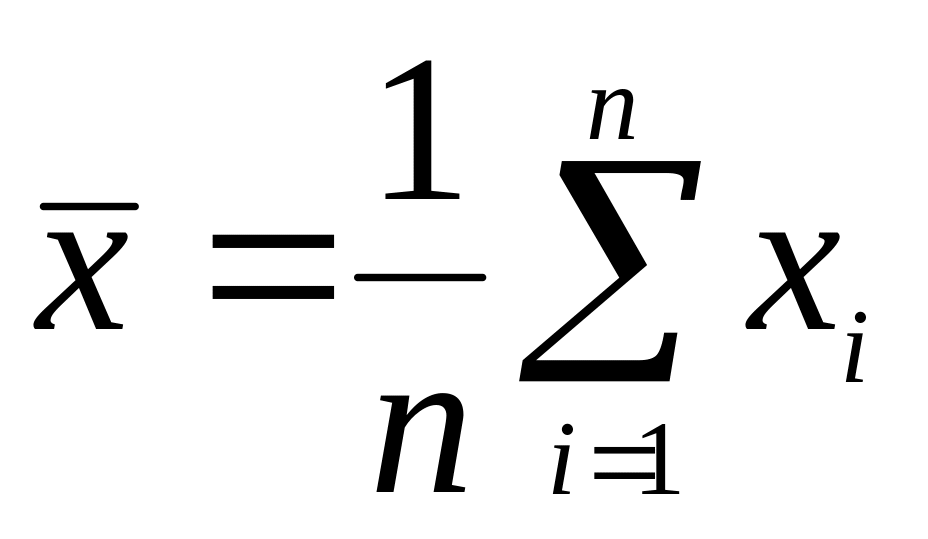 ,
,
где
![]() объем выборки
объем выборки
![]() .
.
В том случае, когда математическое ожидание известно, реализация точечной оценки дисперсии СВ определяется по формуле:
![]() =
=
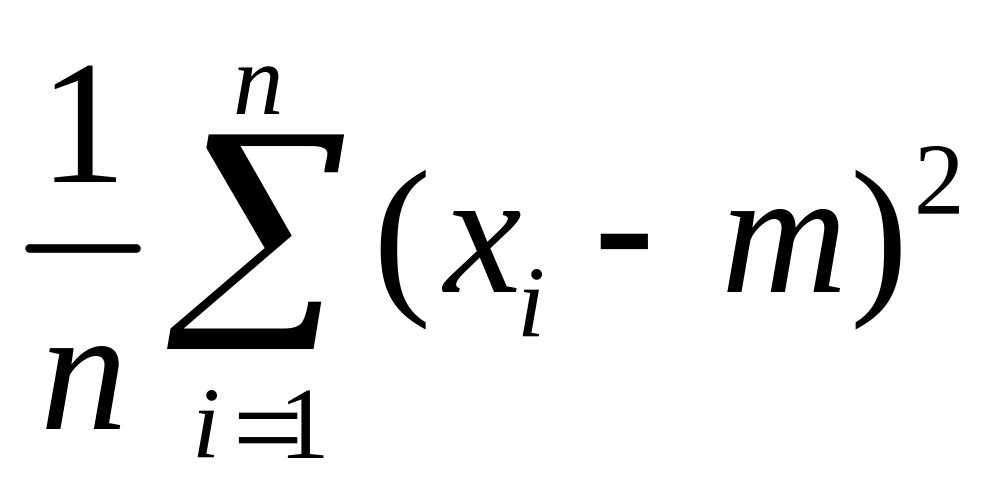 .
.
Если
математическое ожидание
неизвестно, то в качестве математического
ожидания определяется его оценка
![]() .
В
этом случае, реализация точечной оценки
дисперсии СВ определяется по формуле:
.
В
этом случае, реализация точечной оценки
дисперсии СВ определяется по формуле:
=
![]() .
.
Выборочная
дисперсия характеризует рассеяние
наблюдаемых значений выборки около
среднего значения
![]() .
.
