1.2. Аналитическая запись переключательных функций, разложения функций

Способ, предполагающий перечисление наборов, на которых функция принимает значение 1, удобен для функций, имеющих небольшое число единиц в таблице истинности. В некоторых случаях существенно упростить задание функции удается с помощью аналитической записи, когда переключательную функцию представляют в виде некоторой логической формулы. Строго говоря, при рассмотрении аналитических представлений фактически мы имеем дело не с переключательными функциями, а с представляющими их формулами, которых значительно больше, чем переключательных функций, поскольку каждой переключательной функции соответствует множество формул. Обычно множество различных формул, соответствующих рассматриваемой переключательной функции, получают с помощью эквивалентных преобразований, основанных на свойствах булевых алгебр. При этом две формулы считаются эквивалентными, если они представляют одну и ту же переключательную функцию. Следует помнить, что логическая схема реализует переключательную функцию, а структура логической схемы определяется видом формулы, представляющей эту функцию.

Переключательные функции обладают интересными, с точки зрения практического применения, свойствами. Для удобства дальнейшего изложения введем обозначения. Пусть

(1.1)

откуда следует, что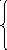

при ,

при .

Произведения вида называют конъюнкциямиl переменных и записывают в векторной форме следующим образом: . В такой записи вектор переменных определяет, какие переменные образуют конъюнкцию, а наборзадает порядок расстановки знаков инверсии над ними. Например:К_(0,1,0,1) (x₁,х₂,х₃,х₄) = .

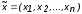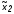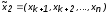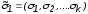Разобьем вектор переменных на два подвектораи таким образом, чтобы подвектор состоял изk, а подвектор изn - k переменных: и. Такому разбиению вектора переменных соответствует разбиение вектора значенийтакже на два подвектора:и.

Любую переключательную функцию, зависящую от n переменных, можно представить в виде дизъюнктивного разложения по k < n переменным:

по всем наборам

или в развернутом виде

по всем наборам

Следствие. Любую переключательную функцию можно представить в виде дизъюнктивного разложения по k = n переменным:

по всем наборам

или в развернутом виде

(1.2)

по всем наборам

Выражение вида называют дизъюнкцией / переменных и обозначают:.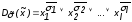

Любую переключательную функцию, зависящую от n переменных, можно представить в виде конъюнктивного разложения по kn переменным:

по всем наборам

или в развернутом виде

по всем наборам

Cледствие. Любую переключательную функцию можно представить в виде конъюнктивного разложения по k = n переменным:

(1.3)

по всем наборам

Полученные в настоящем параграфе разложения являются основой для построения аналитических выражений переключательных функций.

1.3. Совершенные дизъюнктивные и конъюнктивные нормальные формы

Прежде чем перейти к изучению аналитических форм записи, рассмотрим две простейшие функции: элементарную конъюнкцию и элементарную дизъюнкцию, которые часто называют конституентами единицы и нуля соответственно.

Элементарной конъюнкцией n переменных или конституентой единицы называется выражение, представляющее собой конъюнкцию всех n переменных, причем каждая переменная может входить либо в прямом, либо в инверсном виде. Согласно принятым обозначениям элементарную конъюнкцию можно записать так: . Из этой записи следует, что существует всего 2ⁿ различных элементарных конъюнкций n переменных, поскольку каждая конъюнкция определяется одним двоичным набором , состоящим изn компонентов.

В дальнейшем нам потребуется следующее свойство функции (1.1):

1 при ,

0 при .

Справедливость этого утверждения нетрудно проверить с помощью подстановки различных значений х и в выражение (1.1).

Рассмотрим теперь два свойства элементарных конъюнкций. Элементарная конъюнкция равна единице только в том случае, когда наборсовпадает с набором значений переменных. В таблице истинности, задающей элементарную конъюнкцию, должна быть всего одна единица в столбце значений функции. Эта единица расположена в строке, отмеченной двоичным набором, совпадающим с набором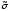. Таким образом, каждому набору в таблице соответствует единственная элементарная конъюнкция, равная единице на этом наборе. Для того чтобы построить эту элементарную конъюнкцию, нужно расставить инверсии над переменными согласно заданному набору. Например, конъюнкция, равная единице на наборе (0,1,1,1,0), имеет вид:.

Конъюнкция двух различных элементарных конъюнкций n переменных равна нулю: .

Элементарной дизъюнкцией n переменных или конституентой нуля называется выражение, представляющее собой дизъюнкцию всех переменных, причем каждая переменная может входить либо в прямом, либо в инверсном виде. Согласно принятым обозначениям условимся обозначать элементарные дизъюнкции следующим образом:

()=....

Из такой записи видно, что существует 2ⁿ различных элементарных дизъюнкций.

Два набора называются противоположными, если все компоненты одного из них можно получить с помощью инверсии компонентов другого набора. Например, наборы ₁=(₁,₂,₃,₄,₅) и 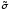₂=(₁,₂,₃,₄,₅) противоположны. Элементарная дизъюнкция () равна нулю только в том случае, когда набор является противоположным набору значений переменных.

В таблице истинности, задающей элементарную дизъюнкцию, должен быть всего один нуль в столбце значений функций. Этот нуль расположен в строке таблицы, отмеченной набором, противоположным набору . Следовательно, каждому набору соответствует единственная элементарная дизъюнкция, равная нулю на этом наборе. Для того чтобы построить эту дизъюнкцию, нужно инвертировать компоненты заданного набора и расставить знаки над переменными согласно противоположному набору. Например, дизъюнкция, равная нулю на наборе (0, 1, 1, 1, 0), имеет вид:.

Дизъюнкция двух различных элементарных дизъюнкций n переменных равна единице:

.

Любую переключательную функцию на основании (1.2) можно представить в совершенной дизъюнктивной нормальной форме (СДНФ), и притом, единственным образом, в следующем виде:

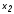(,, ...,) =... (1. 4)

по всем наборам, где (,,...,) = 1.

Покажем единственность СДНФ. Каждому набору , для которого() = 1, соответствует единственная элементарная конъюнкция. Следовательно, совокупности наборов, на которых функция равна единице, соответствует единственная совокупность элементарных конъюнкций, являющаяся СДНФ заданной функции.

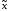Любую переключательную функцию можно представить в совершенной конъюнктивной нормальной форме (СКНФ), и притом, единственным образом. Поскольку инверсия функции () равна единице на тех наборах, на которых () равна нулю, то СДНФ для () можно записать

следующим образом:

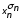(,, ...,) =... (1.5)

по всем наборам, где (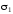,,...,)= 0

Найдем инверсию правой и левой части выражения (1. 5):

(,, ...,) =

по всем наборам, где (,,...,)= 0

Применяя дважды к полученному выражению правила де Моргана, получаем:

() = ( ... ).

по всем наборам, где (,,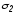...,)= 0

Последнее выражение и является СКНФ. Единственность СКНФ следует из единственности СДНФ.

ПРИМЕЧАНИЕ. СКНФ по аналогии с СДНФ можно получить также на основании разложения (1.3).

Пример 1.1. Построить СДНФ и СКНФ для функции из табл. 1.6:

Таблица 1.6

0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

Для построения СДНФ выпишем все наборы, на которых функция y равна 1: 000, 010, 101, 110. Для каждого набора построим элементарную конъюнкцию, равную единице на этом наборе:, , , . Соединяя эти конъюнкции знаками дизъюнкции, получаем СДНФ заданной функции: .

Для построения СКНФ выписываем все наборы, на которых функция y равна нулю: 001,011,100,111. Для каждого набора построим элементарную дизъюнкцию, равную нулю на этом наборе: , ,,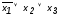. Объединяя с помощью конъюнкции все элементарные дизъюнкции, получаем СКНФ заданной функции:

В заключение отметим, что совершенные нормальные формы не являются самым простым способом задания переключательных функций. Как правило, они допускают преобразование с помощью правил булевой алгебры к более простому виду. Способам построения простейших представлений переключательных функций посвящена следующая глава пособия.