
- •Введение
- •1. Переключательные функции и их свойства
- •1.1. Алгебра переключательных функций
- •1.2. Аналитическая запись переключательных функций, разложения функций
- •1.3. Совершенные дизъюнктивные и конъюнктивные нормальные формы
- •1.4. Графическое и геометрическое представление переключательных функций
- •2. Минимальные формы переключательных функций
- •2.1. Общие положения
Введение
Курс «Дискретная математика» посвящен в основном теоретико-множественному подходу к построению различных математических моделей и, в частности, математическому аппарату анализа и синтеза логических схем без памяти (комбинационных схем). Методы, излагаемые в этом курсе, используются в дальнейшем в курсе “Элементы и узлы вычислительных машин» для описания работы элементов и блоков (функциональных устройств) цифровых машин, в курсе «Цифровые вычислительные машины и системы” для описания взаимодействия отдельных блоков и устройств машины, а также являются базой учебных курсов, посвященных автоматизации проектирования цифровых устройств.
Основной задачей курсовой работы “Реализация переключательных функций в универсальных базисах” является закрепление у студентов теоретических положений курса «Дискретная математика», приобретение практических навыков построения цифровых схем.
В
курсовой работе требуется построить
из элементов универсального структурного
базиса комбинационную схему, выполняющую
преобразование чисел из позиционной
системы счисления с основанием
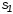 в позиционную систему счисления с
основанием
в позиционную систему счисления с
основанием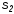 .
.
Курсовая
работа выполняется по индивидуальным
заданиям, которые выдаются руководителем
курсовой работы. В задании указываются
диапазон изменения чисел, основания
исходной (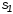 )
и результирующей (
)
и результирующей (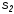 )
систем счисления, параметры двоичного
кодирования на входе и выходе комбинационной
схемы, ограничения, налагаемые на
элементы используемого функционального
и структурного базиса (местность
операторов функционального базиса и
число входов элементов структурного
базиса).
)
систем счисления, параметры двоичного
кодирования на входе и выходе комбинационной
схемы, ограничения, налагаемые на
элементы используемого функционального
и структурного базиса (местность
операторов функционального базиса и
число входов элементов структурного
базиса).
1. Переключательные функции и их свойства
Рассмотрим
множество из двух элементов B(2)
= {0,1} и определим совокупность
переменных (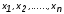 ),
таких, что каждая переменная может
принимать значения только изB(2).
Совокупность таких переменных назовем
вектором двоичных переменных и обозначим
символом
),
таких, что каждая переменная может
принимать значения только изB(2).
Совокупность таких переменных назовем
вектором двоичных переменных и обозначим
символом
 .
Назовем последовательность нулей и
единиц, получающуюся из
.
Назовем последовательность нулей и
единиц, получающуюся из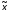 после замены переменных их значениями,двоичным
набором.
Любой такой набор можно рассматривать
как целое двоичное число. Условимся
называть десятичный эквивалент этого
числа номером
набора.
Если обозначить произвольный двоичный
набор символом
после замены переменных их значениями,двоичным
набором.
Любой такой набор можно рассматривать
как целое двоичное число. Условимся
называть десятичный эквивалент этого
числа номером
набора.
Если обозначить произвольный двоичный
набор символом
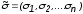 ,
а номер этого набораj(
,
а номер этого набораj(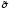 ),
то для заданного
),
то для заданного
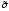 его номер вычисляется следующим образом:j(
его номер вычисляется следующим образом:j(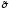 )=
)=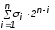 .
.
Например, номер набора j(0, 1, 0, 1, 0, 1) = 24 + 22 + 20 = 21. Наборы из n компонентов нумеруются числами от 0 до 2n - 1. Следовательно, всего имеется 2n различных двоичных наборов.
Двоичный
набор
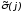 полностью определяется своим номеромj
и числом компонентов n.
Например, для j
= 12 и n=
6 имеем
полностью определяется своим номеромj
и числом компонентов n.
Например, для j
= 12 и n=
6 имеем
 (12) = (0,0,1,1,0,0).
(12) = (0,0,1,1,0,0).
Далее,
введем функции, зависящие от вектора
аргументов
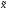 ,
которые обозначим
,
которые обозначим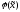 или
или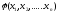 ,
и условимся, что такие функции могут
принимать значения только из множестваB(2)
и называются переключательными
функциями.
Областью определения переключательной
функции от n
переменных является множество из 2n
двоичных наборов. Для того чтобы задать
переключательную функцию, нужно указать
соответствие между этими наборами и
значениями функции. Такое соответствие
проще всего описать с помощью таблицы
истинности,
число строк в которой определяется
числом наборов, а число столбцов на
единицу больше числа переменных. Пример
такой формы задания функции приведен
в табл. 1.1. Обозначим множество
переключательных функций, зависящих
от n
аргументов: Р
(n)
= {
,
и условимся, что такие функции могут
принимать значения только из множестваB(2)
и называются переключательными
функциями.
Областью определения переключательной
функции от n
переменных является множество из 2n
двоичных наборов. Для того чтобы задать
переключательную функцию, нужно указать
соответствие между этими наборами и
значениями функции. Такое соответствие
проще всего описать с помощью таблицы
истинности,
число строк в которой определяется
числом наборов, а число столбцов на
единицу больше числа переменных. Пример
такой формы задания функции приведен
в табл. 1.1. Обозначим множество
переключательных функций, зависящих
от n
аргументов: Р
(n)
= {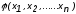 },
и найдем число элементов этого множества
|Р
(n)|,
т. е. число различных переключательных
функций от n
аргументов. В случае табличного задания
столбцы значений различных функций
должны иметь различие хотя бы в одной
строке. Следовательно, для того чтобы
найти число различных функций n
переменных, нужно подсчитать, какое
количество различных столбцов значений
может быть в таблице, имеющей 2n
строк. Если каждую позицию в столбце
считать двоичной переменной, то задача
сводится к определению числа наборов
для 2n
переменных. Исходя из этого, получаем,
что |Р
(n)|
=
},
и найдем число элементов этого множества
|Р
(n)|,
т. е. число различных переключательных
функций от n
аргументов. В случае табличного задания
столбцы значений различных функций
должны иметь различие хотя бы в одной
строке. Следовательно, для того чтобы
найти число различных функций n
переменных, нужно подсчитать, какое
количество различных столбцов значений
может быть в таблице, имеющей 2n
строк. Если каждую позицию в столбце
считать двоичной переменной, то задача
сводится к определению числа наборов
для 2n
переменных. Исходя из этого, получаем,
что |Р
(n)|
=
 .
.
Зависимость числа переключательных функций от числа переменных показана в табл. 1.2:
Таблица 1.1
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
|
1 Из табл. 1.2 видно, что число переключательных функций очень быстро растет при незначительном увеличении числа переменных. |
1 |
1 |
1 |
Таблица 1.2
|
n |
|Р (n)|
|
|
1 |
4 |
|
2 |
16 |
|
3 |
256 |
|
4 |
65536 |
|
5 |
|
