2.9 Синтез комбинационных схем с несколькими выходами. Схемы с разветвлениями. Совместная минимизация

Математической моделью комбинационной схемы (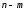полюсника) является система изm переключательных функций от переменных:

Возможные подходы к минимизации такой системы функций:

– раздельная минимизация, при которой каждая из ПФ системы минимизируется отдельно; далее каждой из минимальных форм сопоставляется схема без ветвлений, являющаяся частью комбинационной схемы;

– совместная минимизация, при которой в процессе минимизации учитываются свойства всей системы ПФ как единого целого. Подобный подход может дать более простую комбинационную схему КСх за счет использования общих подформул в формулах, соответствующих различным функциям системы.

Совместная минимизация по методу Квайна - Мак-Класки.

Этап 1. Вначале для каждой функции системы находится множество минималей (простых импликант). Затем эти множества, в общем случае пересекающиеся, объединяются в множество минималей системы ПФ. Следует иметь в виду, что минимали функции могут склеиваться с минималями функцииили поглощаться ими, однако эта операция на данном шаге не применяется!

Этап 2. Для каждой функции системы ищутся альтернативные неизбыточные ДНФ как результат покрытия конституент 1 данной функции множеством минималей всей системы ПФ. Очевидно, что в покрытие могут войти минимали, общие с другими функциями.

Заключительной операцией является выбор совокупности тупиковых ДНФ для , обладающей минимальной сложностью (минимального покрытия системы ПФ). Очевидно, что это минимальное покрытие системы будет в максимальной степени использовать общие импликанты, в том числе не являющиеся минималями для некоторых функций системы.

Минимальному покрытию системы ПФ при наличии общих импликант будет соответствовать схема с ветвлениями, в которой выход элемента 1-го яруса, реализующего общую импликанту, соединяется с несколькими входами элементов второго яруса по числу вхождений этой общей импликанты в покрытия отдельных функций системы.

При минимизации на картах Карно это соответствует выделению смежных областей, общих для нескольких карт. Общим смежным областям соответствуют общие импликанты (не обязательно минимали с точки зрения минимизации отдельной функции!).

Результат совместной минимизации удобно представлять в виде обобщенной таблицы покрытий, строки которой соответствуют импликантам (интервалам), входящим в покрытие системы, а столбцы – отдельным функциям системы. Если -я импликанта входит в покрытие функции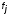, в соответствующей клетке таблицы ставится 1, в противном случае - прочерк. Сложность покрытия системы по Квайну равна сумме рангов всех интервалов с рангамиплюс сумма единиц во всех столбцах таблицы, содержащих не менее 2-х единиц.

Пример 2.11. Необходимо минимизировать систему 3-х переключательных функций от 3-х переменных, заданных множествами единичных наборов:

Выполним вначале раздельную минимизацию функций системы.

	1	0	0	0			1	1	0	0			1	1	0	0
	0	0	0	0			0	1	0	0			0	1	1	1

Минимальные покрытия функций системы имеют вид:

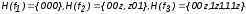
со сложностью соответственно

Отметим что это не единственный вариант минимальных покрытий функций системы. Альтернативное покрытие возможно для функции за счет использования минималивместо минимали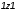. Минимальные покрытия в этом случае имеют вид:

со сложностью соответственно

Теперь выполним совместную минимизацию. Множество минималей системы как результат объединения множеств минималей отдельных функций системы, имеет вид: .

Построим избыточную обобщенную таблицу покрытий системы функций.

Ранг импликант	Импликанты	Функции
3	000	1	1	1
2	00z	–	1	1
2	Z01	–	1	1
2	1z1	–	–	1
2	11z	–	–	1

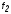Следует обратить внимание на то, что общая, для всех трех функций импликанта не является минималью для функциии, поскольку поглощается интервалом {000,001}, соответствующим минимали , общей для функцийи.

Однако при совместной минимализации выгодно использовать эту общую для всех трех функций импликанту 000, что позволяет отказаться от использования импликанты . Минимальное совместное покрытие будет иметь вид:

	1	0	0	0			1	1	0	0			1	1	0	0
	0	0	0	0			0	1	0	0			0	1	1	1

Результат совместной минимизации представим обобщенной таблицей минимальных покрытий:

Ранг импликант	Импликанты	Функции
3	000	1	1	1
2	z01	–	1	1
2	11Z	–	–	1

Сложность минимальной совместной системы функций: =(3+2+2)+(2+3)=7+5=12. Первое(7) и второе(5) слагаемые в этой оценке соответствуют числу входов элементов на 1-м и 2-м ярусах комбинационной схемы КСх соответственно. Таким образом, сложность минимальной совместной системы ПФ на 6 единиц меньше сложности раздельной системы минимальных ПФ. Схема с разветвлениями, соответствующая минмальной совместной системе функций, приведена на рис.2.7.