Разложение числа в цепную дробь

a>b

. . .

a<b

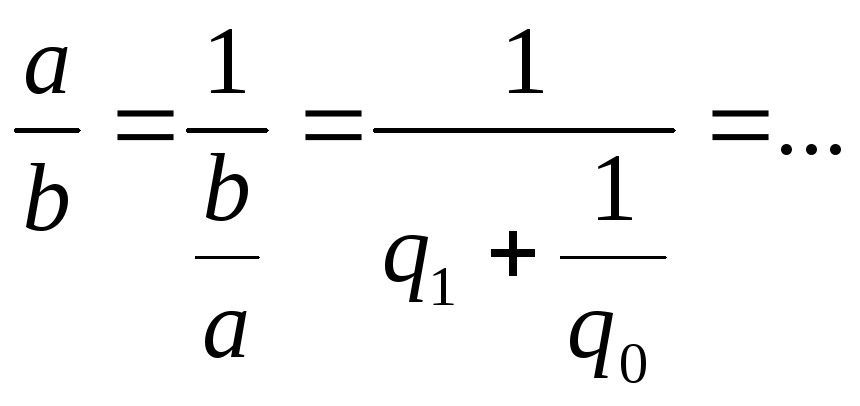
a/b<0

Теорема: 6

Любое рациональное число можно разложить в цепную дробь, одним и только одним способом, где все q_i>0, i>=1, a последнееq_k>1

(Еслиq_k не>1то 2 разл: (q₀,q₁,…,q_k-1,1)

ZR имитируем алгоритм Евклида для вещественного числа

Z=q₀+₁ q₀=[Z] – выделим целую часть числа

_(0,1), Z₁>1

Z=q₀+1/Z₁ (разложение числа в цепную дробь)

Z₁=q₁+₂ q₁=[Z₁]

_(0,1)

Z₁=q₁+1/Z₂, Z₂>1

Z₂=q₂+₃

….

=q₀,q₁…q_k+1

Пример:

(5,(3,2,10)) т.е. цепная периодическая дробь

a=bq₀+r₀

b=r₀q₁+r₁

r₀=r₁q₂+r₂

… …

r_k-2=r_k-1q_k+r_k

r_k-1=r_kq_k+1

D(a,b)=r_k=r_k-2 -r_k-1q_k=r_k-2-(r_k-3-r_k-2q_k-1)q_k=…=ax+by

1. y₀=0, y₁=1, y_i+1=y_i-1-q_k+1-i

D(a,b)=ax_k+2+by_k+2

X_i+1=y_i

Рекуррентная последовательность

d=ax+by

76501=29719 2+17063

29719=17063 1+12056

17069=12056 1+4407

12056=4407 2+3842

4407=3842 1+565

3842=565 6+452

565=452 1+113

453=113 4

76501x+29719y=113

по формуле 1 находим y

d 1 6 1 2 1 1 2

y 1 –1 7 –8 23 –31 54 –139

y=-139 x=54

обрываем процесс на 1 шаге, 2 и т.д.

_=q₀

_=q₀+1/q_1…

_=q₀+1/q₁+1/q_2… подходящие дроби

Вычисление подходящих дробей

_k=-P_k/Q_k – подходящая дробь

Найдем формулы для вычисления P_k Q_k

Вводим условную дробь _=1/0 т.е.P_-1,Q_-1=0

		1	2	3	4	5	6	7	8
Qs		2	1	1	2	1	6	1	4
Ps	1	2	3	5	13	18	121	139	677
Qs	0	1	1	2	5	7	47	54	263

h_s=P_sQ_s-1-Q_sP_s-1

(q_sP_s-1+P_s-2)Q_s-1-(q_sQ_s-1+Q_s-2)

P_s-1=P_s-2Q_s-1-Q_s-2P_s-1=-(Q_s-2P_s-1-P_s-2Q_s-1)=-h_s-1

h_s=-h_s-1=(-1)²h_s-2=…=h₀(-1)^s

h₀=-1, h_s=(-1)^s+1

;

Q_-1=0; Q₁=1; Q₂=q₂Q₁+Q₀ (последующиеQ_i монотонно возрастают)

h_s=(-1)^S+1=(Q_s-1P_s-P_s-1Q_s)

P_sQ_s || d делятся наd=1

D(P_s-2,Q_s)=1 взаимно просты

R

=q₀+₁ q₀=[]

_=q₁+₂ q₁=[_]



_S=q_S+_S+1

подпоследовательность нечетных дробей убывает

подпоследовательность четных дробей возрастает

;

=(5,(3,2,3,10)) =5,29150267

0,0001 1/Q_S²<0,0001 => Q_S>100

		1	2	3	4	5	6	7
Qs		5	3	2	3	10	3	2
Ps	1	5	16	37	127	1037	4018	9403
Qs	0	1	3	6	24	247	465	1777

16/3=5,3(3)

37/7=5,2857

127/24=5,2915

1037/247=5,2915

Теорема: №7

Пусть b<=Q_s=>bQ_s+1<=Q_s+1Q_s=>|a Q_s+1-b P₊₁|<1 = 0

; b<=Q_s+1>Q_s

Диафантовы уравнения

ax+by=c a,b,c,x,yZ x,y - ?

Теорема:8

d=D(a,b) уравнениеax+by=c разрешимо <=> c||d при этом множество решений описывается следующими уравнениями

x=x₀-(b/d)t

y=y₀-(a/d)t tZ

Если существует (x₀,y₀) – частное решение.

Доказательство:

1. Существует если a||d тоb||d , тогда есть решение еслиc||d

Пусть a=de₁; b=de₂; c=de₃ => ax₀+by₀=d имеет решение –x₁,y₁

a(e₃x)+b(e₃y)=c решение есть -(e₃x, e₃y)

2. Пусть существует x₀,y₀ : ax₀+by₀=c

a(x-x₀)+b(y-y₀)=0 <=> Числовое тождество<=> (a/d)(x-x₀)=-(b/d)(y-y₀)

((a/d);(b/d))=1 (иначеd не НОД)

-(b/d)(y-y₀)|| (a/d) => y-y₀=(a/d)t => y=y₀+(a/d)t

аналогично x=x₀+(b/d)t,т.е. если существует решениеx,y то отношение имеет такой вид.

Доказательство в обратную сторону, в результате подстановки получается тождество.

Дополнение: ax+by=c разрешимо, если D(a,b)=1

Пример 1:

15x+19y=1

19=15 1+4

15=4 3+3

4=3 1+1

3=1 3

q 1 3 4

0 1 -1 4 -5

x₀=-5 x=-5+19t

y₀=4 y=-(-4+15t)

126x-102y=18

D(126,102)=6

21x-3y=3

ax+by=D(a,b)

Решим 21x-17y=1 для этого решим 21x+17y=1

21=17 1+4

17=4 4+1

4=4 1

q 4 1

0. 1 –4 5

21(+4)-17(+5)=1

21(-4)-17(-5)=1

x₀=-5 x=-4 3=12

y₀=-4 y=-5 3=15

Общее решение : x=-12+17t

Теорема:9

a₁x₁+a₂x₂+…+a_nx_n=С <=> С||D(a₁a₂ …a_n) Если ???||D => С||D

Доказательство:

1) C=d c По методу математической индукции

a₁x₁+a₂x₂+…+a_nx_n=d =D(a₁a₂ …a_n)

докажем, что всегда разрешимо при любых n.

n=2 a₁x₁+a₂x₂=d =D(a₁,a₂) разрешимо (база)

2) Индукционный переход. Докажем для n+1

a₁U₁+a₂U₂+…+a_nU_n+a_n+1U_n+1 =D(a₁a₂ …a_n, a_n+1)=D(d, a_n+1)=

dy+a_n+1U_n+1=

_ _ _ _ _

(y, U_n+1), гдеd=a₁x₁+a₂x₂+…+a_nx_n

a₁(y,x₁)+a₂(y,x₂)+…+a_n(y,x_n)+ a_n+1U_n+1=