2 Фундаментальные циклы графа

Пространство подграфов

Зафиксируем некоторое множество и рассмотрим множество всех графов с множеством вершин . Буквой будем обозначать пустой граф из этого множества: .

Для графов и из определим их сумму по модулю (в дальнейшем в этом разделе будем называть ее просто суммой) как граф , где обозначает симметрическую разность множеств и . Иначе говоря, ребро принадлежит графу тогда и только тогда, когда оно принадлежит в точности одному из графов и . Пример показан на рис. 7.1.

Рис. 7.1. 

Следующие свойства введенной операции очевидны или легко проверяются.

Коммутативность: для любых и .

Ассоциативность: для любых .

.

.

Отсюда следует, что множество относительно операции образует абелеву группу. Нейтральным элементом ("нулем") этой группы служит граф , а противоположным к каждому графу является сам этот граф. Уравнение с неизвестным и заданными графами и имеет единственное решение . Благодаря свойству ассоциативности мы можем образовывать выражения вида , не используя скобок для указания порядка действий. Легко понять, что ребро принадлежит графу тогда и только тогда, когда оно принадлежит нечетному количеству из графов .

Рассмотрим множество из двух элементов . Оно является полем относительно операций умножения и сложения по модулю 2. Определим операцию умножения элементов этого поля на графы: , для любого графа . Множество с введенными операциями сложения графов и умножения на элементы поля является линейным векторным пространством.

Зафиксируем некоторый граф и рассмотрим множество всех его остовных подграфов, которое будем обозначать . Это множество состоит из элементов, среди них сам граф и граф . Оно замкнуто относительно сложения графов и умножения на элементы поля, следовательно, является подпространством пространства . Его называют пространством подграфов графа .

Любой граф из может быть выражен как сумма однореберных подграфов. Всего у графа имеется однореберных подграфов и они, очевидно, линейно независимы. Следовательно, однореберные подграфы образуют базис пространства , а размерность этого пространства равна .

В пространстве можно очень естественным способом ввести координаты. Занумеруем ребра графа : . Теперь остовному подграфу можно поставить в соответствие характеристический вектор его множества ребер:

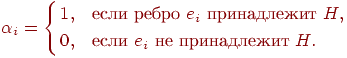
Получаем взаимно однозначное соответствие между множеством и множеством всех двоичных векторов с координатами. Сумме графов соответствует векторная (покоординатная) сумма по модулю 2 их характеристических векторов.

Компактное представление пространства дает его базис. Если выписать все простые циклы графа , то это в большинстве случаев не будет его базисом, так как некоторые из этих циклов могут быть суммами других. Построить базис пространства , состоящий из простых циклов, можно следующим образом. Выберем в графе какой-нибудь каркас . Пусть - все ребра графа , не принадлежащие . Если добавить к ребро , то в полученном графе образуется единственный (простой) цикл . Таким образом, получаем семейство из циклов, они называются фундаментальными циклами относительно каркаса .

Теорема. Множество всех фундаментальных циклов относительно любого каркаса графа образует базис пространства циклов этого графа.

Доказательство. Зафиксируем некоторый каркас и рассмотрим фундаментальные циклы относительно этого каркаса. В каждом из этих циклов имеется ребро , принадлежащее данному циклу и не принадлежащее никакому из остальных. Поэтому при сложении этого цикла с другими фундаментальными циклами данное ребро не "уничтожится" - оно будет присутствовать в суммарном графе. Следовательно, сумма различных фундаментальных циклов никогда не будет пустым графом, то есть фундаментальные циклы линейно независимы.

Покажем теперь, что любой квазицикл графа является суммой фундаментальных циклов. Действительно, пусть - такой квазицикл. Пусть - все ребра , не принадлежащие . Рассмотрим граф . Каждое из ребер , , входит ровно в два слагаемых этой суммы - в и в . Следовательно, при сложении все эти ребра уничтожатся. Все остальные ребра, присутствующие в графах-слагаемых, принадлежат . Значит, - подграф графа . Так как все слагаемые являются квазициклами, значит, - тоже квазицикл. Но в нет циклов, поэтому имеется единственная возможность: , откуда получаем .

Из этой теоремы следует, что размерность пространства циклов графа равна числу ребер, не входящих в его каркас. Так как каркас содержит ребер, где - число компонент связности графа, то эта размерность равна . Это число называют цикломатическим числом графа.