§ 5 Метод Эйлера численного решения задачи Коши

Пусть функции непрерывны в прямоугольной области

Из теоремы существования (§2) следует:

1) в некоторой окрестности существует единственное решениеу(х) задачи Коши ;(1)

2) через каждую точкуМ(х,у) этой окрестности проходит «своя» интегральная кривая, причем ДУ определяет касательную прямую к этой интегральной кривой:tg(α_kac)=f(x,y).

Постановка задачи:«найти приближенное значениеy*(x*)решенияy(x*)задачи Коши (1) в точке».

Для нахождения приближенного значения у*(x*) разделим промежуток[ x₀,x*] точкамиx_0,x_i= x₀+ih; i=1:n наn равных частей с шагомh=(x*-x₀)/n.

1)За приближенное значение решения задачи Коши в точке х₁=x_o+h примем ординату касательной к интегральной кривой в точке М₀ : . Известно, что погрешность такой замены .

2) Повторив аналогичные построения для точки М₁, примем за приближенное значение решения в точкеx₂=x₁+h :

3) Очевидно, что общая формула подобной «по-шаговой» итерационной процедуры метода Эйлера имеет вид: 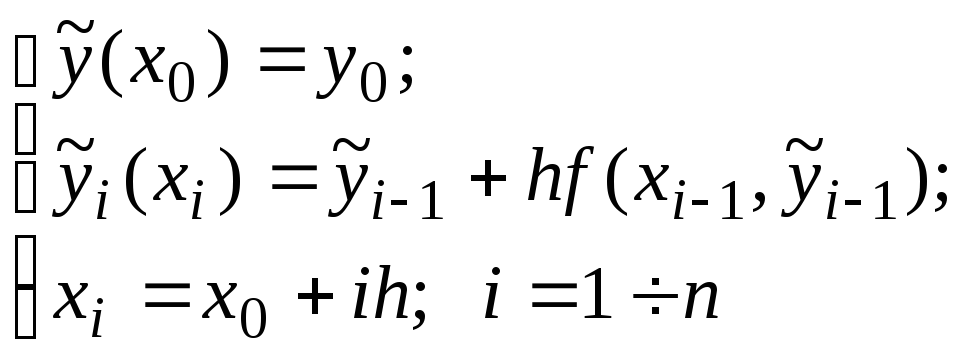и приближенное значение

Замечания.

1) Геометрически метод Эйлера численного решения задачи Коши сводится к замене на промежутке [x₀,x*] интегральной кривойy(x) «ломаной Эйлера», составленной из отрезков касательных к соответствующим интегральным кривым в точках разбиенияx_i=x_o+ih.

2) На практике для получения приближенного значения с заданной погрешностью εиспользуют «алгоритм измельчения разбиений отрезка [x₀;x]”:

- Вычисляют значение при разбиении с шагомh1.

- Вычисляют значение при разбиении с шагомh2=h1/2и сравнивают модуль разностис заданной погрешностьюε.

= процедуру измельчения продолжают до тех пор, пока для двух последовательных разбиений не будет выполнено неравенство

==================================================================

§ 6 Типовой расчет по теме «Численное решение задачи Коши».

Задание. Исследовать существование и единственность решения задачи Коши

и методом Эйлера найти с заданной погрешностьюEPSприближенное значение решения в точкеx_k=x₀+0.25, используя равномерное разбиение интервала [X₀,X_k] с начальным шагомh=0.05.

_{[I] Так как функции непрерывны в R}²_{, задача Коши имеет единственное решение.}

_{[II] Введем равномерное разбиение промежутка [0;0.25] на n частей с шагом h=0.25/n : x0; xi=i∙h; i=1,2,..,n и выполним вычисления по рекуррентной формуле:}

_{для nk =5∙k;k=1,2,.., последовательно удваивая количество интервалов разбиения до тех пор, пока не будет выполнено неравенство ∆k= |y5k-y5(k-1)|≤EPS.}

_{Заметим, что все промежуточные вычисления следует выполнять в «полной разрядной сетке».}

_{В таблице приведены результаты вычислений для n1=5 и n2=10, округленные до 10}^-5_.

i		xi	yi		f(xi,yi)		h∙f(xi,yi)
n1	n2
0	0	0.00	0.90000		0.19000		0.00475
	1	0.025		0.90475		0.20517		0.00475
1	2	0.050	0.90950	0.90988	0.22060	0.21987	0.01103	0.00513
	3	0.075		0.91538		0.23410		0.00550
2	4	0.10	0.92053	0.92123	0.24920	0.24790	0.01246	0.00585
	5	0.125		0.92743		0.26129		0.00620
3	6	0.15	0.93.298	0.93396	0.27600	0.27426	0.01380	0.00653
	7	0.175		0.94082		0.28686		0.00686
4	8	0.20	0.94678	0.94799	0.3011	0.29907	0.01506	0.00717
	9	0.225		0.95547		0.31091		0.00748
5	10	0.25	0.96184	0.96324				0.00777

_{Так как ∆y=|0.96324-0.96184|=0.00140<EPS=0.002, итерационный процесс прекращаем.}

_{Результат: y(0.25)≈ 0.96324}