§3 Линейные дифференциальные уравнения 1 порядка (лду); метод вариации постоянной.

Напомним, что уравнение называется линейным относительно переменных u,v, если сумма степеней этих переменных в каждом слагаемом равна 1 или 0:au+bv=cLY(u,v). Пустьy(x) – дифференцируемая функция иy’,dy– ее производная и дифференциал.

Определение.

ЛДУ 1 порядка с коэффициентами a(x), b(x) и правой частью f(x) называется ДУ вида

Если f(x), q(x)≡0, уравнение называется «однородным ЛДУ (ОЛДУ)», в противном случае его называют «неоднородным ЛДУ». Очевидно, что для всякого неоднородного ЛДУ можно записатьсоответствующее емуОЛДУ.

Можно показать, что задача Коши для ЛДУ с непрерывными коэффициентами имеет единственное решение при любом начальном условии y(x₀)=y₀.

1. Рассмотрим сначала однородное ЛДУ и найдем его общее решение :

Заметим, что общее решение ОЛДУ имеет вид У_o(x,C)=CF(x) () и при С=0 включает частное решение У_о(х)≡0.

2) Решение неоднородного ЛДУ y’(x)+p(x)=q(x) будем искать «методом вариации постоянной»-в видеy(x)=C(x)F(x), гдеF(x) – решение соответствующего ОЛДУ(F^/+p(x)F(x)≡0), аС(х)-неизвестная дифференцируемая функция. После подстановкиy(x)=C(x)F(x) в ЛДУ для С(х) получим ДУРП:

Таким образом,

• решение неоднородного ЛДУ сводится к последовательному решению двух ДУРП, первое из которых является соответствующим однородным ЛДУ;

• общее решение неоднородного ЛДУ равно аддитивной сумме общего решения соответствующего ОЛДУ Y₀(x,C), которое не зависит от правой части q(x), и частного решения y*(x) неоднородного ЛДУ, которое определяется как решением ОЛДУ, так и правой частью ЛДУ:Y_Н (x,C)=Y₀(x,C)+y*(x)

Замечание.Структура решения ЛДУ соответствует фундаментальному свойству линейного физического объекта: его движение (состояние) складывается из «внутреннего движения» (Y₀(x,C)) и движенияy*(x) под действием «возмущения»q(x), при этомвозмущение не влияет на внутреннее движение.

Рассмотрим пример решения ЛДУ

Найдем решение задачи Коши с начальным условием

Замечания.

[1] Если ДУ записано «в дифференциалах», его решение можно искать либо как функцию y(x),либо как функциюx(y).“Свободу выбора” удобно использовать, если относительно одной из этих функций ДУ оказывается линейным.

1) (x-2xy-y²)dy+y²dx=0 x(1-2y)dy+y²dx=y²dy--- ЛДУ(x(y),dx)

2)x²dy+(3-2xy)dx=0 x²dy-2xydx=-3dx; --- ЛДУ(y,dy)

3) (8y+10x)dx+(5y+7x)dy=0 – не ЛДУ, но однородное:

[2] ДУ Бернулли приводится к ЛДУ(U,dU), если ввести функциюU(x)=y^1-n ЛДУ(U,U’)

ДЗ Определить тип ДУ; найти его общее решение и решение задачи Коши с начальным условиемy(1)=2 .

ОЛДУ(x,dx)Xo(y,C)=Cy²e^1/y;C(y)=C+e^-1/y;

§4 Ду 1 порядка «в полных дифференциалах».

Напомним, что для дважды непрерывно-дифференцируемой функции F(x,y):

1)

2)

3)

Определение. ДУ «в полных дифференциалах» называется ДУ 1 порядка

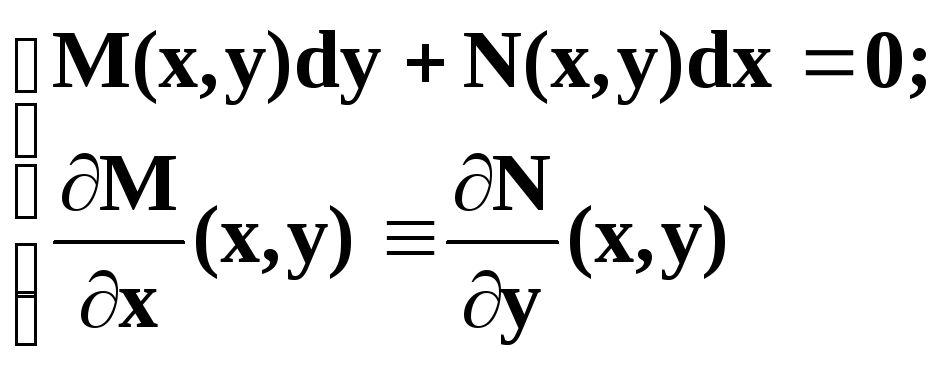(1)

Рассмотрим дважды непрерывно дифференцируемую функцию двух переменных F(x,y):

Из (1) и (2) следует, что обыкновенное ДУ (1) равносильно ДУ в частных производных

(3)

решение которого dF(x,y)=0 F(x,y)=C являетсяобщим интегралом для исходного ОДУ.

Известно, что решение системы (3) нажодится в два этапа:

(а) После интегрирования любой из частных производных искомая функция F(x,y)находится “с точностю ” до произвольной функции C(y) одной переменной.

б)Подстановка полученного результата во второе уравнение системы дает для этой функции ОДУ 1 порядка :

Общий интеграл исходного ДУ «в полных дифференциалах» записывается в виде:

Например, ДУ (2x+3yx²)dx+(x³+3y²)dy=0 является ДУ «в полных дифференциалах», так как:

Найдем функциюF(x,y):

Д/З: Найти общий интеграл ДУ e^ydx+(xe^y-2y)dy=0