Глава Обыкновенные Дифференциальные Уравнения (ДУ) 1

§1 Дифференциальные уравнения : основные понятия, примеры. 1

§2 ДУ 1 порядка с разделяющимися переменными 3

§3 Линейные дифференциальные уравнения 1 порядка (ЛДУ); метод вариации постоянной. 8

§4 ДУ 1 порядка «в полных дифференциалах». 12

§ 5 Метод Эйлера численного решения задачи Коши 14

§ 6 Типовой расчет по теме «Численное решение задачи Коши». 16

§7 Системы ЛДУ 1 порядка с постоянными коэффициентами; операционный метод решения задачи Коши. 17

Глава Обыкновенные Дифференциальные Уравнения (ДУ)

§1 Дифференциальные уравнения : основные понятия, примеры.

Пусть nраз дифференцируемая функцияkпеременных (вD_fопределеныnфункцийf^(m)(x),m=0,1,..,nи (n-1) из них непрерывны).

Определение 1. Дифференциальным уравнением (ДУ) порядка “n” называется уравнение;, связывающее аргументх, функциюfи ее производные функции , порядок старшей из которых равен“n”, при этом ДУ относительнофункции одной переменной(к=1) называют«обыкновенным ДУ», а ДУ относительнофункции нескольких переменных(k>1) и ее частных производныхназывают «ДУ в частных производных» .

Например, (1) xy^//+2y^/+xy=x; (2)y”=x - обыкновенные ДУ второго порядка.

(3) 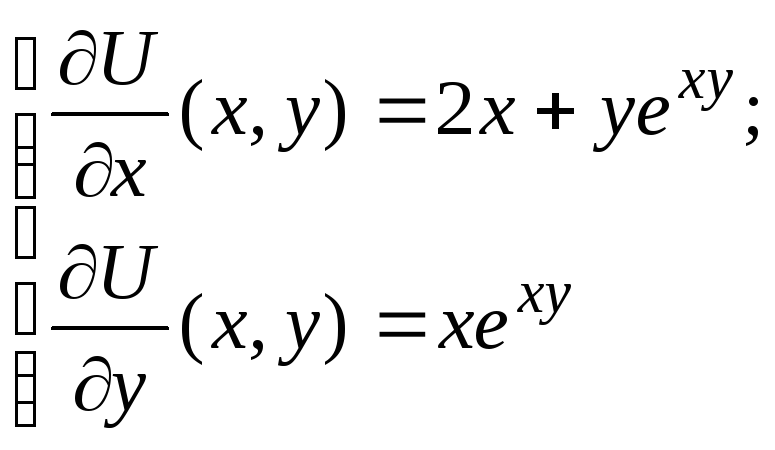- система двух дифференциальных уравнений в частных производных первого порядка относительно дифференцируемой функцииU(x,y) двух переменных.

Определение 2.Дифференцируемая функцияf, подстановка которой обращает ДУ в тождество в области , называетсярешением ДУ. График решения ОДУy=f(x) называетсяинтегральной кривой ДУ. Нахождение множества решений ДУ называютинтегрированием ДУ.

Например, функция y₁(x)=1+sin(x)/x является решением ДУ (1), так как

.

Проверьте, что:

• функция y₂(x)=1+cos(x)/x так же является решением ДУ (1);

• множество функций включает все решения ДУ(2);

• функция U(x,y) =x²+xe^xy+1 является решением системы ДУ(3), удовлетворяющим начальному условиюU(1;0)=3.

В дальнейшем будут рассматриваться только обыкновенные ДУ.

Поскольку есть Уравнение, возникают вопросы: 1)существует ли решение?; 2)единственно ли оно?; 3) как найти множество решений?

Рассмотрим несколько примеров.

1) Известно, что ДУ первого порядка y^/(x)=f(x):(а) имеет решение для любой кусочно непрерывной (интегрируемой) функцииf(x)и это решениеy=F(x) называется первообразной для функцииf; (б) существует бесчисленное множество решений и (в) это множество называется неопределенным интегралом , содержит одну аддитивную произвольную константу и соответствующие интегральные кривые представляют семейство параллельных гладких линийy=F(x)+C, причем через каждую точку проходит единственная интегральная криваяy=F(x)+(y₀-F(x₀).

Например,

2) Найдем множество решений ДУ 2 порядка

Это множество содержит двепроизвольные константы, фиксированные значения которых С₁=С₀, С₂=D₀определяют единственную интегральную кривуюy(x,C₀,D₀)=x³/6+C₀x+D₀, проходящую через точкуM₀(x₀,y₀);y₀=x₀²/6+C ₀x₀+D₀, тангенс угла наклона которой в этой точке равенtg(α₀)=y’(x₀,C₀)=x₀²/6+C₀^.

Определение 3. Решениеf(x)ДУ порядка “n”, удовлетворяющее “n” начальным условиям , называетсярешением задачи Коши с начальнымиусловиями:Например, функцияf(x)=x²/2+1 является решением задачи Коши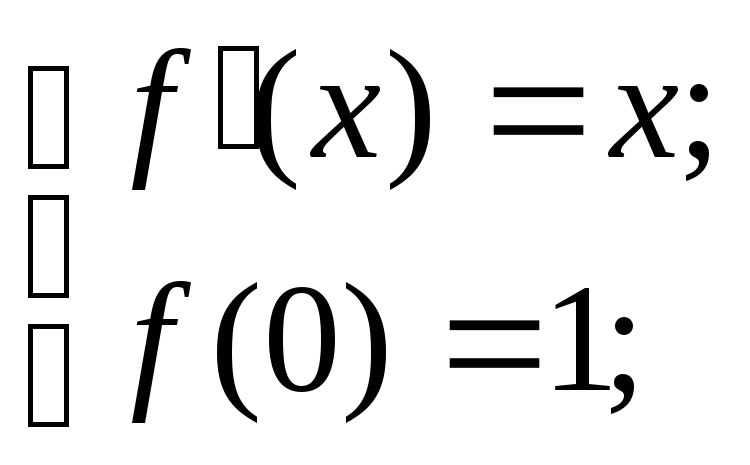

Найдем решение задачи Коши для ДУ 2 порядка :

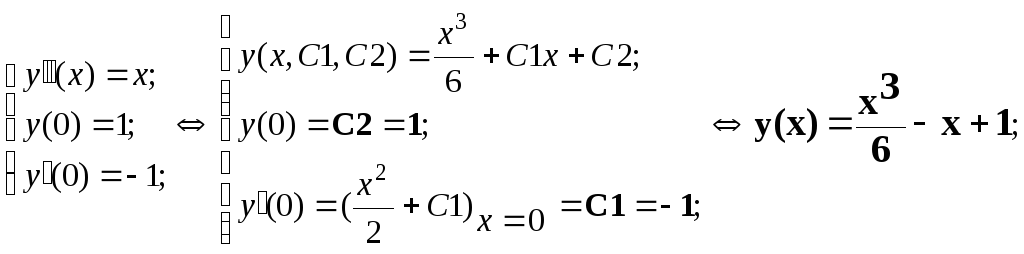
ЭКЗ. Для ДУ 2 порядка найти: 1)множество решений; 2)решение задачи Коши с начальными условиями :