
- •Вопрос 1. Обобщающие статистические показатели.
- •Вопрос 2. Статистическая сводка и группировка.
- •Вопрос 3. Статистика уровня жизни.
- •Вопрос 1. Счета бухгалтерского учета и их строение.
- •Вопрос 2. Типы хозяйственных операций и их влияние на бухгалтерский баланс.
- •Логическая структура бухгалтерского баланса.
Статистика
Вопрос 1. Обобщающие статистические показатели.
Данные, полученные в результате статистического наблюдения, сводки и группировки, подлежат дальнейшей обработке и анализу путем вычисления обобщающих показателей. Для выражения размеров и количественных соотношений явлений в статистике применяются абсолютные и относительные величины.
С помощью метода обобщающих показателей решается одна из важнейших задач правовой статистики: определяется количественная характеристика изучаемой совокупности социально-правовых явлений.
Абсолютные величины и их виды:
Абсолютные величины получают в результате сводки первичного статистического материала. Они характеризуют размеры или объем признака явления применительно к конкретным условиям места и времени.
По способу выражения абсолютные величины делятся на индивидуальные и суммарные.
1. Индивидуальные величины выражают размеры количественных признаков отдельных единиц изучаемой совокупности, например: возраст, доход, заработная плата одного работника и т. д. Их получают в результате статистического наблюдения и отражают в соответствующих учетных документах. Они являются основой для осуществления в последующем группировок различных видов.
2. Суммарные величины выражают величину того или иного признака для всех единиц изучаемой совокупности или отдельных ее групп. Их получают в результате суммирования индивидуальных абсолютных величин или подсчета количества единиц совокупности.
Статистические абсолютные величины всегда являются именованными числами и выражаются в определенных единицах измерения. В правовой статистике различают натуральные, стоимостные и трудовые единицы измерения (рис. 1).
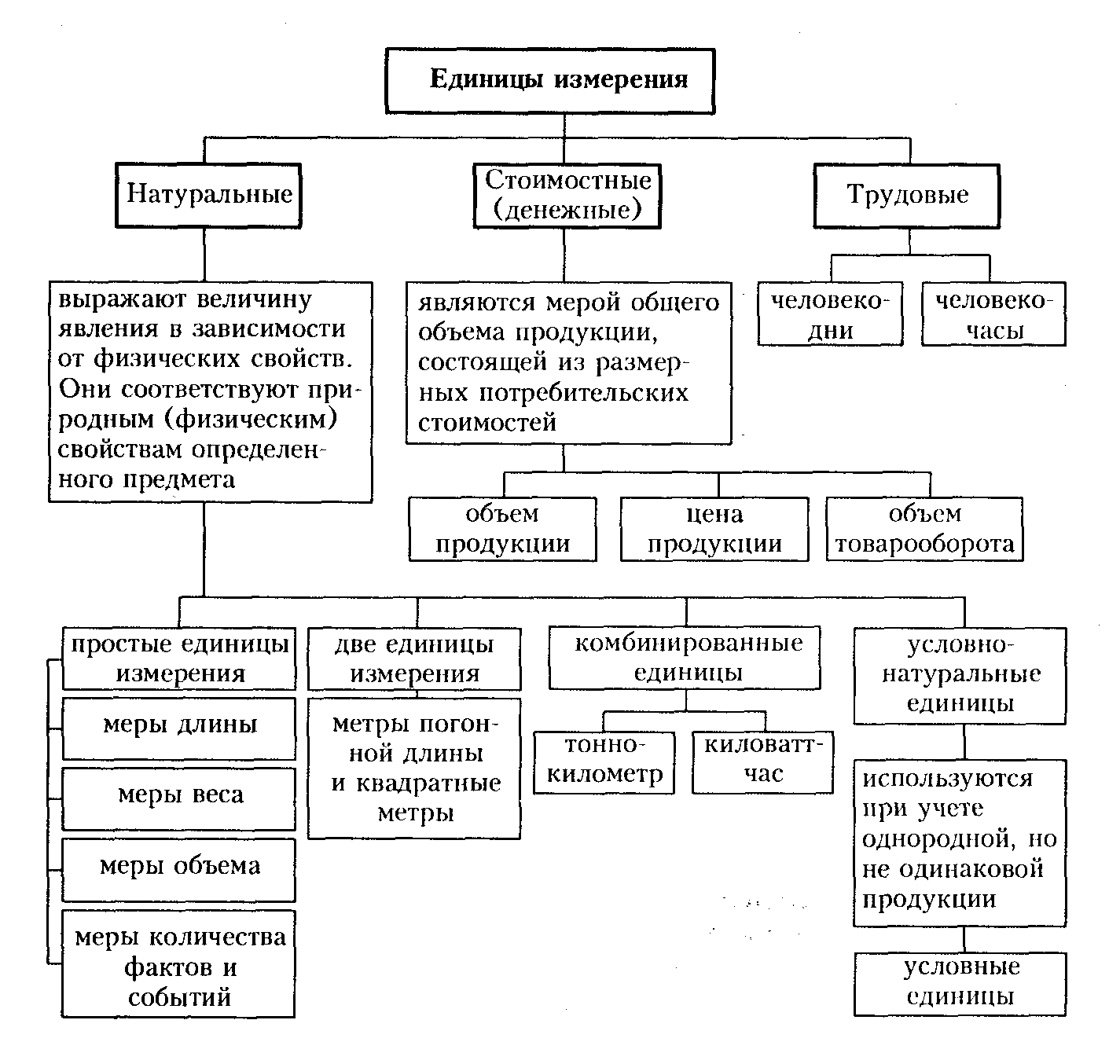
Рис 1. Единицы измерения
Абсолютные величины имеют практическое и познавательное значение. Они выражают размеры различных правовых явлений, характеризуют движение материальных ценностей, служат основой экономического анализа хозяйственной деятельности, а также всех форм и приемов математического моделирования и прогнозирования развития правовых явлений в будущем.
Относительные величины и их виды:
Для анализа, выявления характерных черт и особенностей изучаемых социально-правовых явлений абсолютных величин недостаточно. Возникает необходимость в сравнениях и сопоставлениях. Для этого используют относительные величины, получаемые в результате деления двух показателей, один из которых — знаменатель — является базой для сравнения.
Относительная величина — это обобщающий показатель, который характеризует соотношение между двумя абсолютными, относительными или средними величинами.
Каждая относительная величина представляет собой дробь, в числителе которой — величина, которую хотят сравнить (данные отчетного периода), а в знаменателе — величина, с которой сравнивают (база сравнения). Относительные величины измеряются в коэффициентах, процентах, промиллях, продецимиллях. Относительная величина может быть выражена и именованными числами (например, плотность населения, количество преступлений, правонарушений на тысячу населения и т. д.).
Таким образом, с помощью относительных величин можно получить обобщающую характеристику изучаемого явления; они облегчают анализ статистических данных, позволяют осуществить сравнительный анализ разнородных явлений, более глубоко изучить взаимосвязи и взаимозависимости различных явлений.
По характеру, назначению и сущности выражаемых количественных соотношений различают следующие относительные величины.
1. Относительные величины динамики характеризуют изменение одноименных явлений во времени на определенной территории. Вычисляются они в результате сопоставления показателей каждого последующего периода с предыдущим или первоначальным. Исходя из этого в статистике применяется базисный и цепной способы вычисления относительных величин динамики.
Базисный
способ характеризует динамику явления
относительно определенного предыдущего
периода. Базисные величины получают
делением абсолютных показателей каждого
периода Yі — на уровень какого-либо
одного периода, принятого за базу
сравнения, — Y0, т. е.
![]() .
Этот способ применяется с целью выявления
какой-либо устойчивой тенденции в
развитии явления за длительное время.
.
Этот способ применяется с целью выявления
какой-либо устойчивой тенденции в
развитии явления за длительное время.
Цепной
способ характеризует динамику явления
относительно предыдущего периода.
Базисные величины получают делением
абсолютных показателей каждого
последующего периода Yі+1, на показатель
предыдущего периода Yі, т. е.
![]() .
Данный способ используется для
анализа и сопоставления показателей
отчетного и предыдущих периодов.
Полученные данные характеризуют,
как явление изменяется от одного периода
к другому.
.
Данный способ используется для
анализа и сопоставления показателей
отчетного и предыдущих периодов.
Полученные данные характеризуют,
как явление изменяется от одного периода
к другому.
2. Относительные величины интенсивности характеризуют степень насыщенности изучаемых явлений в определенной среде, т. е. выявляют распространенность определенного признака в наблюдаемой совокупности. Относительные величины интенсивности вычисляют для установления того, как часто данное явление встречается в среде своего функционирования и жизнедеятельности, какова степень его распространенности.
3. Относительные величины структуры характеризуют состав совокупности и показывают, какой удельный вес в общем итоге составляет каждая ее часть. Эти величины получают в результате деления показателей, относящихся к части совокупности, на показатели всей совокупности.
4. Относительные величины координации характеризуют соотношение частей изучаемой совокупности, которое показывает, во сколько раз сравниваемая часть явления больше или меньше части, принимаемой за базу, сравнения. Они позволяют установить соотношение частей совокупности, т. е. отношение одной части к другой.
5. Относительные величины сравнения характеризуют сравнительные размеры одноименных величин, касающихся одного и того же периода или момента времени, но принадлежащих к разным территориям или объектам.
6. Относительные величины выполнения плана характеризуют степень выполнения плана за определенный период времени. Коэффициент выполнения плана рассчитывается как отношение достигнутого уровня к плановому за один и тот же период времени:
КВ.П. = (Фактический объем) / (Плановый объем) * 100%.
7. Относительные величины планового задания характеризуют изменения плановых показателей по сравнению с фактическими — базовыми для плана и определяются как отношение планового задания на предстоящий период к фактически достигнутому уровню за предшествующий период.
Средние величины и их виды:
К обобщающим показателям кроме относительных величин относятся и средние.
Средней величиной называется обобщающий показатель какого-либо варьирующего признака совокупности однотипных явлений, который характеризует типичный уровень этого признака у единицы совокупности.
Основная особенность использования средних величин заключается в том, что их можно вычислять только для качественно однородных совокупностей.
Выбор формулы средней величины зависит от экономической сущности усредняемого признака, т. е. наличия тех или иных исходных данных. Наиболее распространены в правовой статистике средняя арифметическая и средняя гармоническая величины.
Средняя арифметическая величина применяется тогда, когда объем варьирующего признака представляет собой сумму его индивидуальных значений. Средняя арифметическая может быть простой и взвешенной.
Простая средняя арифметическая величина применяется тогда, когда каждое индивидуальное значение признака встречается один раз или одинаковое количество раз.
Рассчитывается она делением суммы индивидуальных значений признака на их количество по формуле
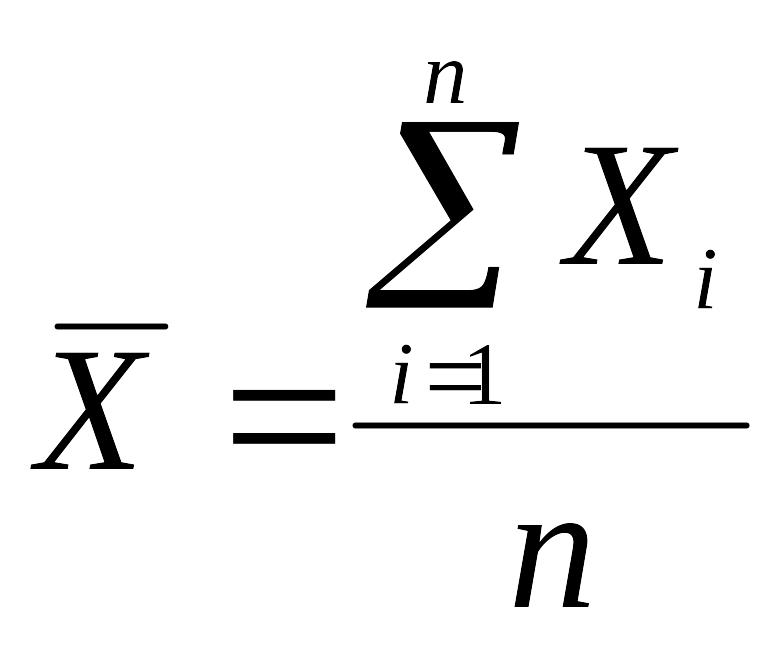 ,
,
где
![]() ,
,
![]() — соответственно среднее и индивидуальное
значение признака; п — количество
индивидуальных значений.
— соответственно среднее и индивидуальное
значение признака; п — количество
индивидуальных значений.
Взвешенная средняя арифметическая величина применяется тогда, когда варианты в изучаемой совокупности повторяются неодинаковое количество раз и вариационный ряд несимметричен. Для вычисления средней арифметической взвешенной необходимо каждую варианту умножить на соответствующую ей частоту и сумму произведений разделить на сумму частот, т. е. формула имеет вид
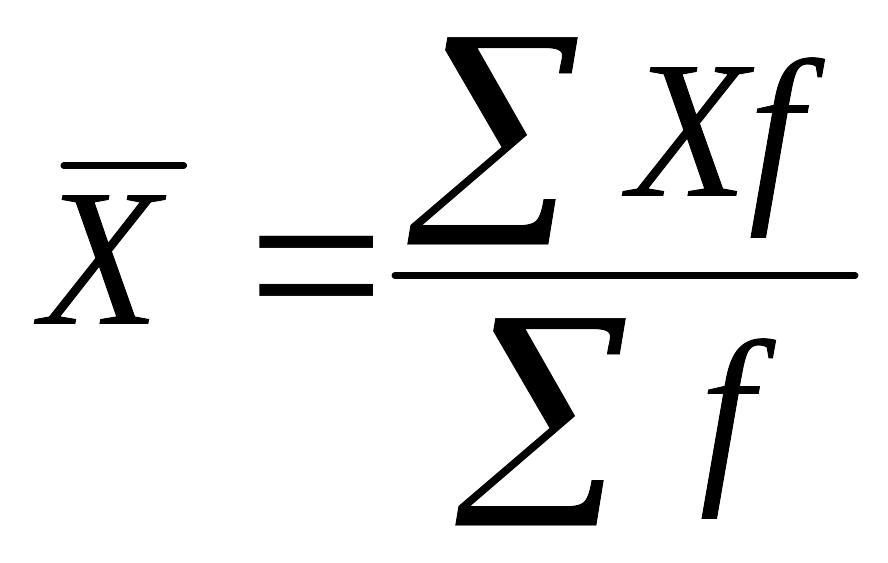 ,
,
где X — варианты; f — частоты.
Средняя гармоническая — это величина, обратная средней арифметической обратных значений признака. Она используется тогда, когда за частоту (вес) принимается не количество единиц совокупности, а величины, которые представляют собой результат умножения вариант на количество единиц, т. е. когда частотами являются показатели, находящиеся в числителе исходного соотношения.
Средняя гармоническая определяется по таким формулам:
простая
—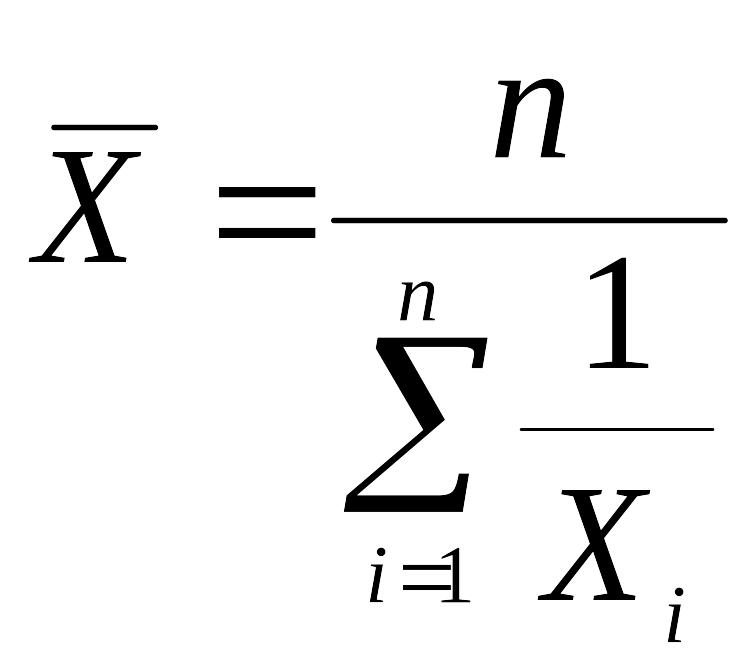 ,
,
взвешенная
—
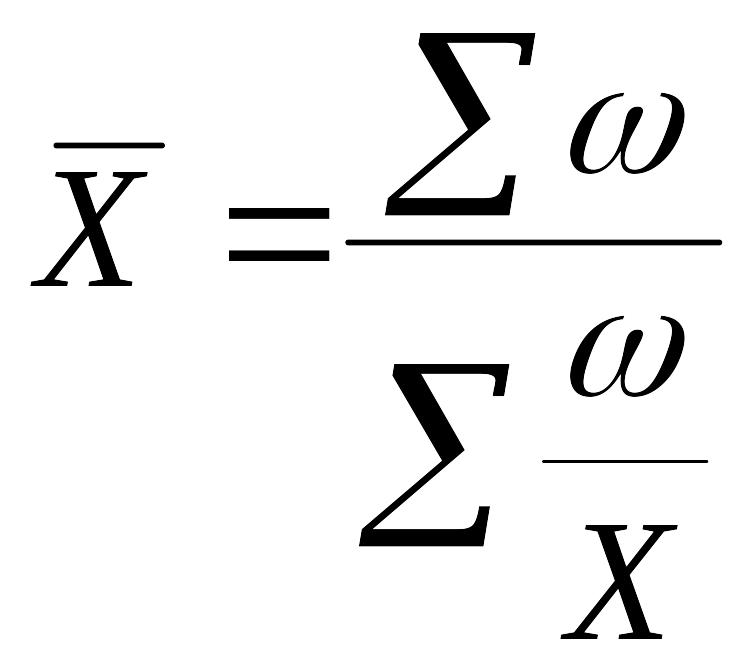 ,
,
где
п — количество вариант;
![]() —
обратное значение варианты; ω —
произведение варианты на частоту, ω=Xf.
—
обратное значение варианты; ω —
произведение варианты на частоту, ω=Xf.
Первая формула используется лишь тогда, когда частота каждой варианты равна единице, т. е. очень редко.
Применение средней арифметической и средней гармонической величин зависит от исходных данных. Если в качестве веса используется произведение; ω, сомножителем которого является определяемый признак, то применяется средняя гармоническая (например, для вычисления средней выработки продукции на одного работающего, среднего процента забракованной продукции). В правовой статистике, как правило, используется средняя арифметическая.
