28.Оцінка статистичної значущості та надійності параметрів em.

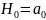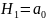Параметри i узаг.ЕМ визначити на практиці неможливо.Параметри вибіркової ЕМ,розр.на основі вибірк.сукупності завжди будуть містити деяку помилку.Важливо оцінити розходж.між параметриами узаг. І вибір. Моделі. Для цього викор. Т-стат.Стьюдента.Форм. основну і альтер.гіпотези. i =0 та i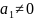 . Якщо основна гіпотеза прийм.,то коеф. i є стат.незначущими і У не залеж від Х.Знаходимо СКВ параметрів моделі. Якщо t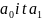 > табл., то основна гіпотеза відх.і прийм. інша i відр. від 0, Х впливає на У.

30.Особливості побудови множ.Em

Для виявл.та оцінки ступеня впливу факторів на резул.величину викор. множинну регресію.

M(Y)=f(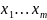 ). Задача багато факт.регрес.аналізу полягає в тому, щоб на основі наявних стат.даних визн.найкр.оцінки параметрів i , перевірити їх стат.надійність та оцінити адекв. Побудованої моделі.Для цього на основі обмеженої вибірки будують вибіркову багатофакторну модель

y=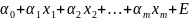 . Параметри i визн. за МНК, мініміз.суму квадратів відхилень модельованих значень від фактичних.

Для оцінки адекв.множ.моделі викор. коеф.множинної кореляції і детермінації.

Ry -хар-зує силу взаємозв. між факт і модел значеннями. - показ.частку заг.дисперсії залеж.змінної У, яка поясн. моделлю.

29.Побудова та аналіз економетричної лінійної моделі з багатьма змінними.

Для того щоб кількісно описати зв’язок між кількома або багатьма змінними, одна з яких є залежною, інші — незалежними змінними, необхіднорозглянути лінійну економетричну модель, яка базується на регресійному

аналізі.Побудуємо модель множинної лінійної регресії.Нехай економетрична модель специфікована у лінійній формі:Y = a₀ + a₁X₁ + a₂X₂ + a₃X₃ + uде a₀, a₁, a₂, a₃ - параметри моделі, u - стохастична складова (залишки), X₁, X₂, X₃ - фактори, Y - показник.

Оцінимо параметри моделі методом МНК:A = (X 'X)^-1X 'Y,де матриця X характеризує всі незалежні змінні моделі. Оскільки модель має вільний член a₀, для якого всі x_i = 1, то матрицю потрібно доповнити першим стовпцем, в якому всі члени є одиницями, X ' - транспонована матриця до даної, а вектор Y - вектор залежної змінної. Таким чином знайдемо 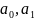… і записуємо модель.