7 Численные ряды, признаки их сх-ти. Абсолютно и условно сх-ся ряды, их св-ва.

Рядом наз. посл-ть .

Числовой ряд – выражение вида , где образуют бесконечную посл-ть.

Суммы , наз частичными суммами ряда, а член - общим членом ряда. Если посл-ть частичных сумм имеет предел (при n ) , то ряд наз-ся сх-ся, а число - суммой ряда. Обознач-е: . Если предела не сущ., то ряд – расх-ся.

Необходимое условие сходимости ряда:

Общий член ряда должен при стремится к нулю: .

Критерий Коши сходимости ряда:

Числовой ряд явл. сх-ся тогда и только тогда, когда для любого >0 существует такое N что для любого и для любого натурального p выполняется: .

Свойства сх-ся рядов:

1. Отбрасывание конечного числа начальных членов ряда или присоединение в начале его нескольких новых членов не отражается на поведении (сх-ти или расх-ти) ряда.

2. Если члены сх-ся ряда умножить на один и тот же множитель с, то его сходимость не нарушится.

3. Сх-ся ряды можно почленно складывать и вычитать: из сходимости ряда с суммой и с суммой следует, что ряд сх-ся и его сумма равна .

Числовые ряды с положительными членами

, - числовой ряд с положительными членами.

Признаки сходимости:

1. Признак сравнения. Если два ряда и имеют положительные члены и, начиная с некоторого n, , то из сходимости первого ряда следует сходимость второго, а из расходимости второго ряда следует расходтмость первого.

2. Признак сравнения в предельной форме. Если существует придел 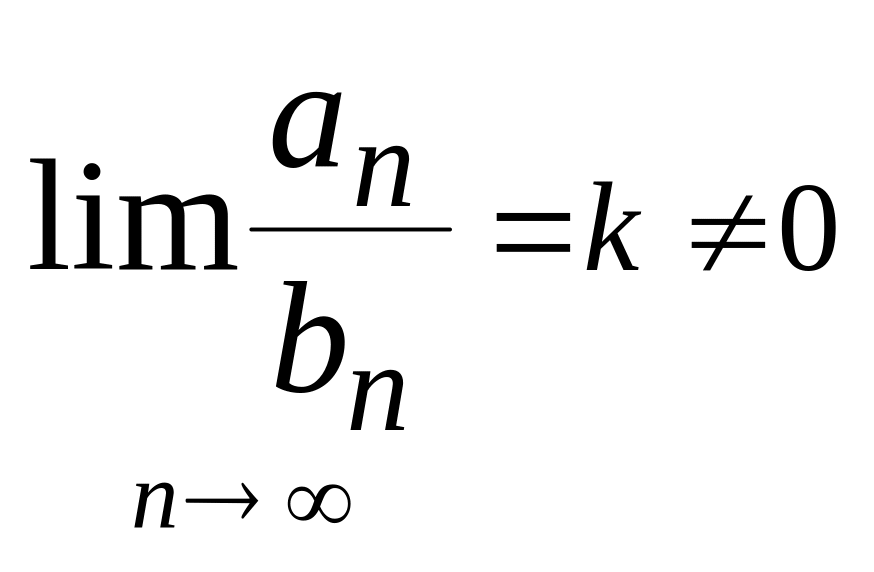. Тогда первый ряд эквивалентен второму (т.е. ведут себя одинаково).

3. Интегральный признак Коши-Маклорена. Пусть ф-я 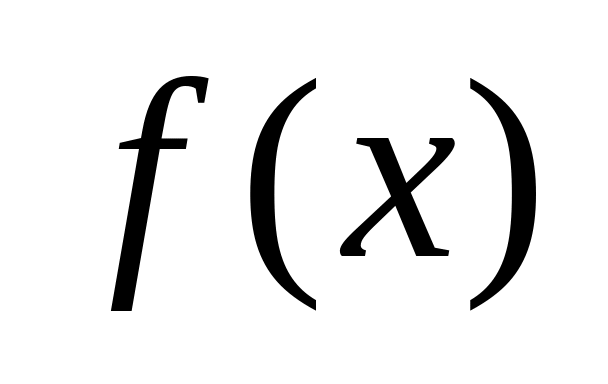неотрицательна и невозрастает на [1,+ ), тогда ряд 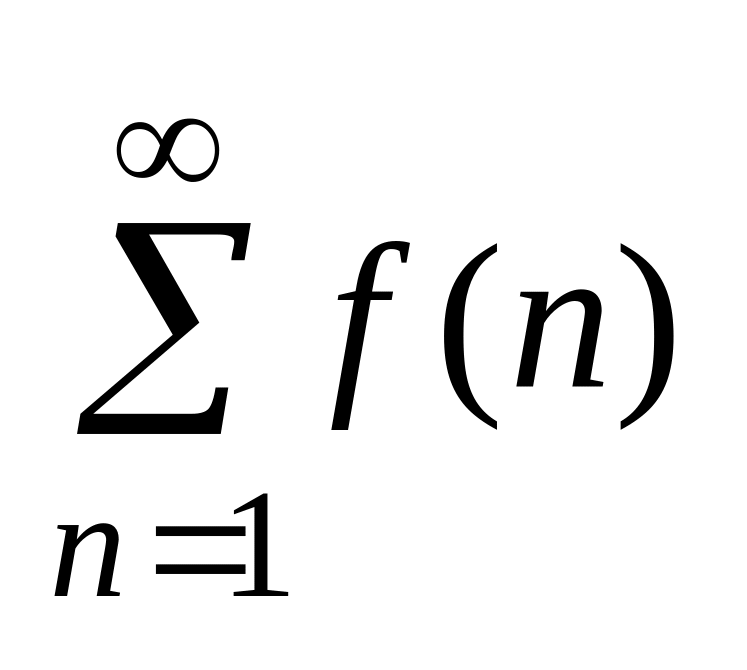и 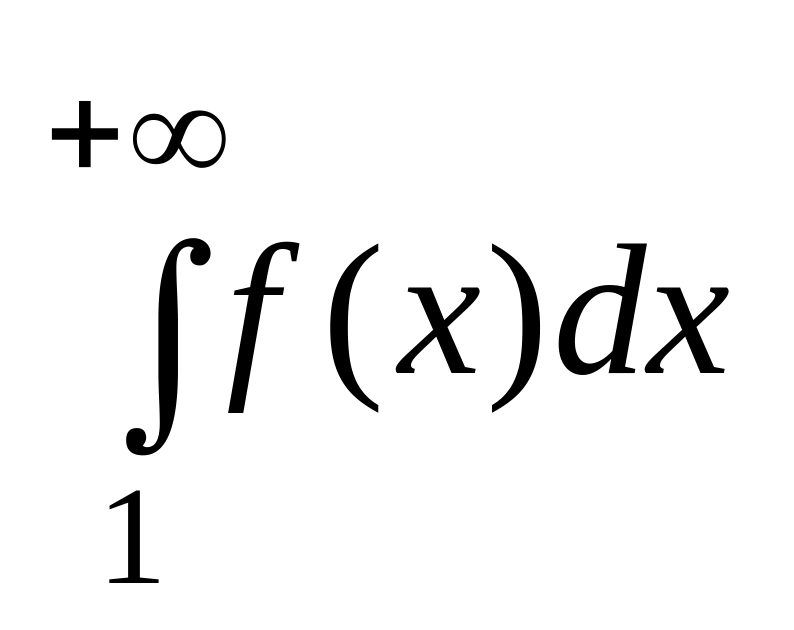ведут себя одинаково. (ф-я невозрастает на (а,b), если для любых 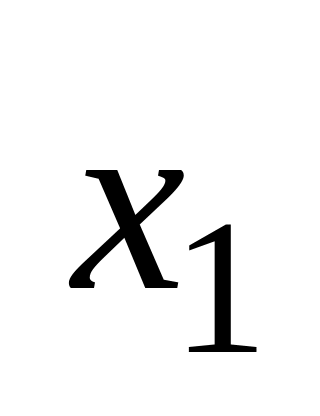и : : ).

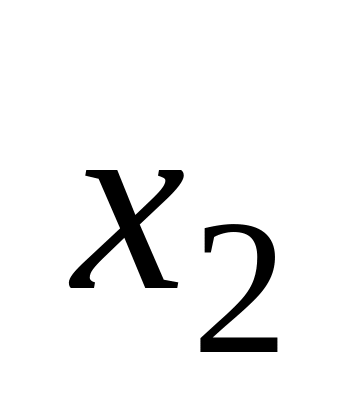
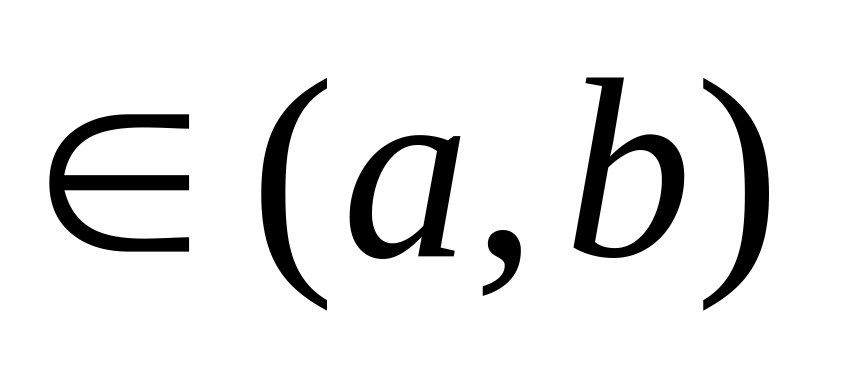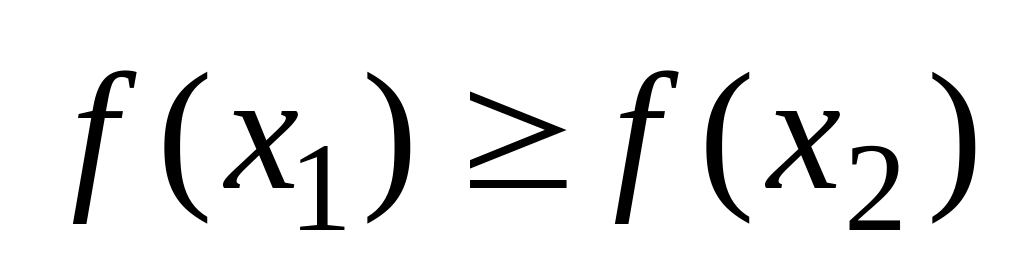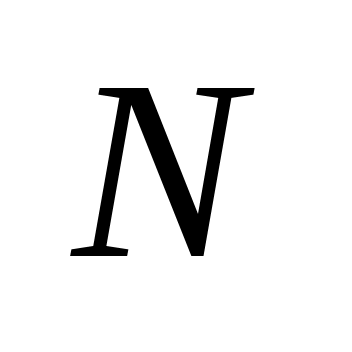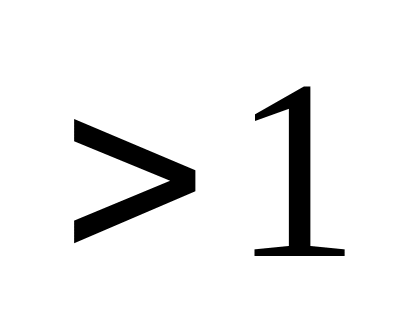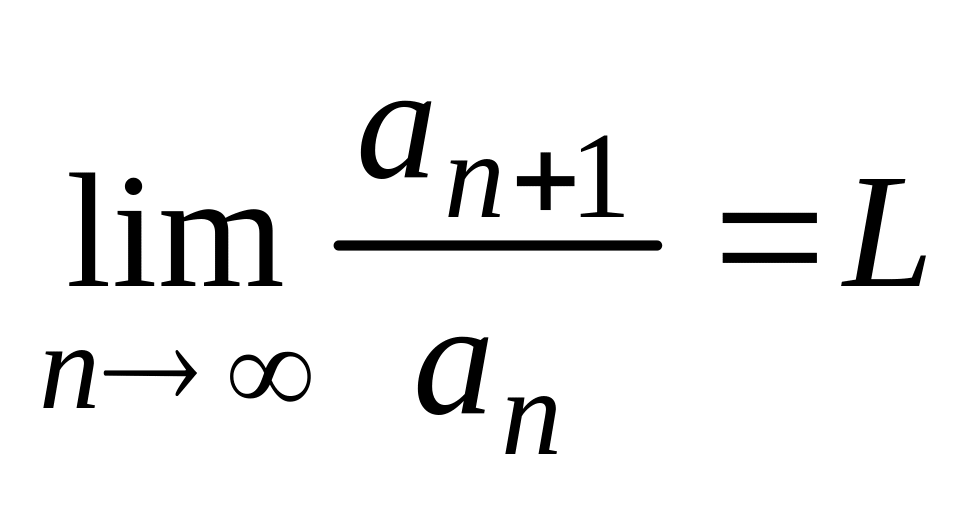4. Признак Даламбера. 1) Если начиная с некоторого номера для любого вып-ся ,то ряд – сх-ся, если это отношение , то ряд – расх-ся. 2) Если , то при - ряд сходится, при - ряд расх-ся, - нельзя сказать.

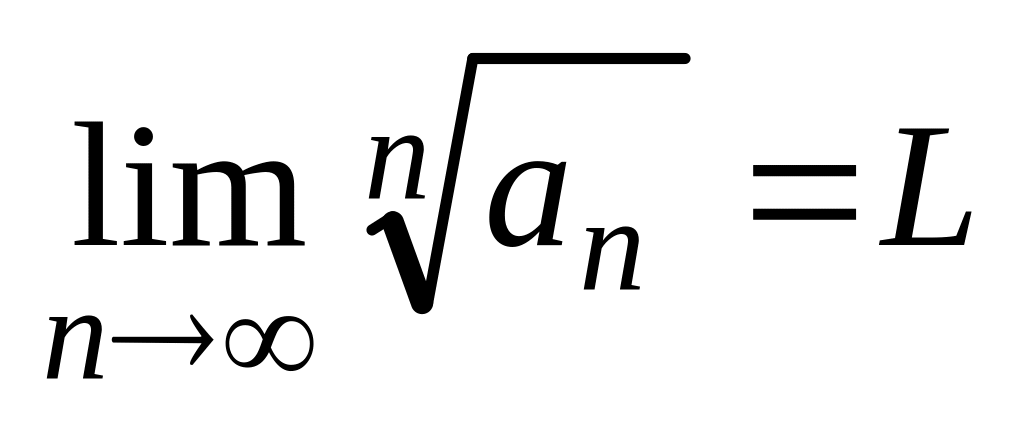5. Признак Коши. 1) Если начиная с некоторого номера для любого вып-ся ,то ряд – сх-ся, если это отношение , то ряд – расх-ся. 2) Если , то при - ряд сх-ся, при - ряд расх-ся, - нельзя сказать.

Абсолютная и условная сходимость.

Одновременно с рядом , члены которого имеют неодинаковые знаки (знакопеременный ряд), удобно рассматривать ряд , составленный из абсолютных величин членов первого ряда. Если второй ряд сх-ся, то и первый сх-ся; в этом случае первый ряд наз-ют абсолютно сх-ся. Если же второй ряд расх-ся, то первый ряд может расх-ся, но может и сх-ся; в последнем случае он называется условно сх-ся.

Свойства абсолютно сх-ся рядов.

1. В абсолютно сх-ся ряде члены можно переставлять местами любым сп-бом; сумма ряда не будет при этом меняться. Переменив же порядок условно сх-ся ряда (т.ч. будет переставлено бесконечное множество членов ряда), можно изменить его сумму, сделать ее равной любому числу и даже сделать ряд расх-ся.

2. Абсолютно сх-ся ряды можно не только почленно складывать и вычитать, но и перемножать, как обыкновенные многочлены, представляя результат в виде ряда.

Знакопеременные числовые ряды

Если - сходится    - сходится.

Признаки сходимости знакопеременных рядов:

1.Признак Дирихле. Пусть - огр., и пусть - монотонно стремится к 0. Тогда - сходится.

2.Признак Абеля. Пусть - огр., и пусть - монотонно и огр.. Тогда - сх-ся.

3.Признак Лейбница. Пусть - монотонно стремится к 0 ( >0). Тогда - сходится.

Теорема Дирихле: Если ряд абсолютно сх-ся то любая его перестановка тоже абсолютно сходится к той же сумме.

Теорема Римана: Пусть - условно сх-ся. Тогда Для любого действ. А сущ. такая перестановка ряда , которая сх-ся к этому числу А.

Опр-я:

Предел переменной величины х – постоянное число а, если для каждого наперед заданного произвольно малого положительного числа можно указать такое значение пер-й х, что все последующие значения пер-й будут удовлетворять нер-ву .

Предел ф-и . Функция при , если для каждого , как бы мало оно ни было, можно указать такое , что для всех и удовлетворяющих неравенству , имеет место неравенство . Если -предел функции при , то пишут .

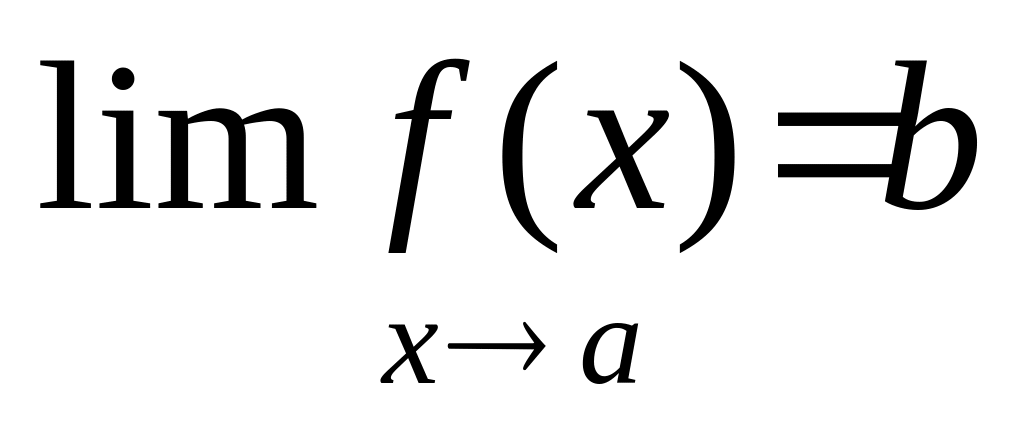Огр. посл-ть – если для заданной посл-ти можно указать такое число , что все без исключения члены последовательности будут .

Монотонные: возрастающие, убывающие, неубывающие, невозрастающие.