9. Магнитное поле в веществе. Условия на границе раздела двух магнетиков.

Намагниченность ,где -магнитный момент магнетика, -магнитный момент отдельной молекулы.

1) Рассматривая характеристики магнитного поля, мы вводили вектор магнитной индукции В, который характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками, и вектор напряженности Н, характеризующий магнитное поле макротоков. => магнитное поле в веществе складывается из двух полей: внешнего поля создаваемого током, и поля, создаваемого намагниченным вещетвом. Тогда вектор магнитной индукции результирующего магнитного поля в магнетике равно векторной сумме магнитных индукций внешнего поля (поля, создаваемого намагничивающим током в вакууме) и поля микротоков (поля, создаваемого молекулярными токами):

где ( - магнитная постоянная).

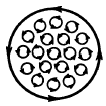Для описания поля, создаваемого молекулярными токами, рассмотрим магнетик в виде кругового цилиндра сечения S и длинны , внесённого в однородное внешнее магнитное поле с индукцией . Возникающее в магнетике магнитное поле молекулярных токов будет направлено противоположно внешнему полю для диамагнетиков и совпадать с ним по направлению для парамагнетиков. Плоскости всех молекулярных токов расположатся перпендикулярно вектору , т.к. векторы их магнитных моментов не параллельны вектору (для диамагнетиков) и параллельны (для парамагнетиков).

Если рассмотреть любое сечение цилиндра, перпендикулярное его оси, то во внутренних участках сечения магнетика молекулярные токи соседних атомов направлены навстречу др. другу и взаимно компенсируются

Некомпенсированными будут лишь молекулярные токи, выходящие на боковую поверхность цилиндра.

Ток, текущий по боковой поверхности цилиндра, подобен току в соленоиде и создает внутри него поле, магнитной индукции которого вычисляется через формулу для магнитной индукции поля внутри соленоида (в вакууме): при N=1(1 виток соленоида), т.е.

Где -сила молекулярного тока, -длина цилиндра, а магнитная проницаемость . - это ток, приходящийся на единицу длины цилиндрара, т.е. его линейная плотность, и следовательно магнитный момент этого тока ,(V-объём магнетика).

P-магнитный момент магнетика объёмом V, а значит - намагниченность магнетика. =>

Из (2)(3)=> или в векторной форме =>



Из опыта: в несильных полях прямо пропорциональна напряжённости поля, вызывающее намагничивание, т.е.

-маг.-я восприимчивость вещ.-ва (безразмерная величина)

из (6) и (4) =>

=>

-маг проницаемость вещества =>

Диамагнетики: . парамагнетики: .

Т.е.

Где и - соответственно суммы макротоков (токов проводимости) и микротоков (молекулярных токов).

Т.о. циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна сумме токов проводимости и молекулярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Вектор характеризует результирующее поле, созданное токами проводимости и микроскопическими токами в магнетиках, поэтому линии не имеют источников и являются замкнутыми.

Теорема о циркуляции вектора :

=>для полного тока , ( - сумма токов проводимости)

=>учитывая(4)

2 )Рассмотрим условия для векторов и на границе раздела двух однородных магнетиков (магнитные проницаемости ₁ и ₂) при отсутствии на границе тока проводимости.

Построим вблизи границы раздела магнетиков 1 и 2 прямой цилиндр очень малой высоты, одно основание в 1 магнетике, а второе во 2. Основания S очень малы => в пределах каждого из них вектор одинаков. По теореме Гаусса

= > , т.к. , то

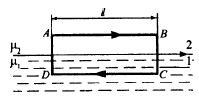
Построим вблизи границы раздела магнетиков 1 и 2 небольшой замкнутый прямоугольный контур ABCDA ( - его длина).

Из (*) => (токов проводимости на границе нет)

=> т.к. знаки интегралов по AB и CD разные (пути интегрирования противоположны), а интегралы по BC и DA очень малы. =>

=>

Т.о., при переходе через границу раздела двух магнетиков нормальная составляющая вектора B(В_n) и тангенциальная составляющая вектора Н(Н_т)

Изменяются непрерывно, а тангенциальная составляющая вектора В(В_т)

И нормальная составляющая вектора Н(Н_n) претерпевают скачок.