Лекции ДиРУр

Дифференциальные и разностные уравнения

1. Введение

1.1. Дифференциальные уравнения. При решении многих научных и практических задач возникают уравнения, содержащие неизвестные функции под знаком производной или дифференциала.

Уравнения, в которых неизвестная функция входит под знаком производной или дифференциала, называются дифференциальными уравнениями.

Решением дифференциального уравнения называется функция, которая при подстановке ее в уравнение обращает его в тождество. Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения. Действительно, задача решения дифференциальных уравнений есть задача обратная к дифференцированию. В качестве примера рассмотрим дифференциальное уравнение вида

Уравнение (1) также можно записать в виде

Из интегрального исчисления известно, что решение уравнения (1) может быть получено в результате интегрирования

по формуле (3) определяется неоднозначно.

Решение уравнения (1) в виде (3), где произвольное постоянное, называ-

ется общим решением. Если при этом каким-либо образом определить константу , то получится так называемое частное решение уравнения (1). Что-

бы в конкретной ситуации определить константу , надо задать некоторые дополнительные условия. Пусть, например, известно, что при неиз-

вестная функция принимает значение . Тогда, полагая получим

1

Пример 1. Материальная точка движется по прямой с постоянным ускорением . Найти закон движения точки.

Решение. Ускорение представляет производную от скорости времени , т.е. . Полученное уравнение можно записать в виде

Для определения константы C2 будем считать, что в начальный момент вре-

мени путь равен s0 . Тогда из (7) находим

s0 0 0 C2 C2 , т.е. C2 s0 .

Таким образом, получаем требуемый закон движения материальной точки

at2

s 2 v0t s0 .

Пример 2. Пусть в банк под % в год положена сумма руб. Требуется оп-

ределить закон изменения вклада при условии, что проценты начисляются непрерывно и построить дифференциальное уравнение, для функции, определяющей этот закон.

2

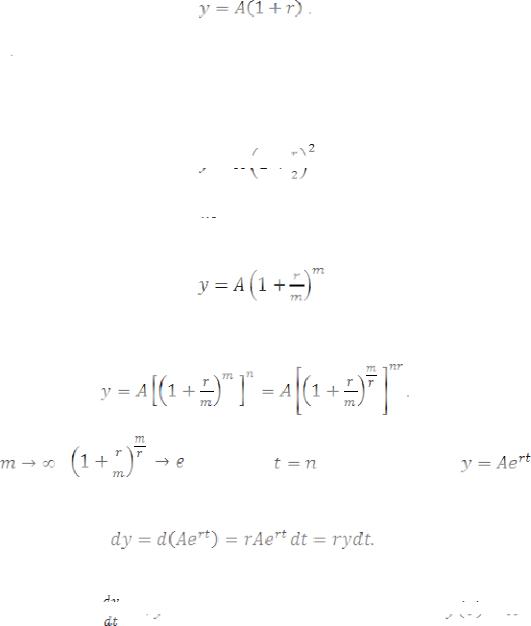
Решение. Если проценты начисляются один раз в год, то по истечении года сумма вклада будет равна

Здесь означает процентную ставку, выраженную в долях.

Если проценты начисляются каждые полгода, то в конце года сумма вклада получится равной

.

Если проценты начисляются раз через равные промежутки времени, то к концу года сумма вклада составит

.

По истечении лет сумма вклада составит

(8)

чение короткого промежутка времени имеем

(9)

Из (9) получаем, что закон изменения вклада описывается дифференциаль-

ным уравнением с заданным начальным условием .

Существуют два основных типа дифференциальных уравнений: обыкновенные, в которых неизвестными функциями являются функции одного переменного, и в частных производных, в которые входят производные искомых функций по нескольким переменным. В данном курсе рассматриваются только обыкновенные дифференциальные уравнения, поэтому в дальнейшем при указании типа дифференциального уравнения слово «обыкновенное» будем опускать.

3

Порядком дифференциального уравнения называется порядок старшей про-

изводной, присутствующей в уравнении.

Говорят, что дифференциальное уравнение записано в нормальной форме, если оно разрешено относительно старшей производной. В противном случае дифференциальное уравнение представлено в общей форме.

Дифференциальное уравнение порядка n называется линейным, если оно имеет вид

Существует огромное количество задач, в которых требуется определить неизвестные функции , , аргумента , удовлетворяющих системе уравнений, содержащих производные этих функций по . Таким образом,

приходят к системам дифференциальных уравнений. Например, закон дви-

жения материальной точки в трехмерном пространстве с заданным вектором скорости в виде функции времени и координат точки определяется решением системы трех дифференциальных уравнений.

Дифференциальное уравнение го порядка легко приводится к системе n

дифференциальных уравнений первого порядка, и наоборот. Это свойство дифференциальных уравнений часто используется при интегрировании дифференциальных уравнений высокого порядка. Система дифференциальных уравнений

4

задает динамическую систему, называемую «гармоническим осциллятором». Её фазовым пространством является плоскость (x,v), где v — скорость точки x. Гармонический осциллятор моделирует разнообразные колебательные процессы — например, поведение груза на пружине. Его фазовыми кривыми являются эллипсы с центром в нуле. С другой стороны, эта система двух дифференциальных уравнений первого порядка эквивалентна дифференциальному уравнению второго порядка

d2 y

dt2 ky.

1.2.Разностные уравнения. В экономике значения величин часто рассматриваются в определенные дискретные моменты времени. Например, когда речь идет о годовом плане производства продукции с отчетностью по каждому месяцу, то удобно значения всех текущих показателей брать соответствующими каждому месяцу. Если рассматривается некоторая величина y, то вме-

сто скорости изменения этой величины берут среднюю скорость за оп-

ределенный конечный интервал времени . Если выбрать масштаб вре-

мени так, что длина рассматриваемого интервала времени равна 1, то скорость изменения y можно представить как разность

yt y(t 1) - y(t),

которую называют правой разностью. В практике также используют левую разность, определяемую как

yt y(t) - y(t 1) yt 1 .

В дальнейшем часто будут использоваться обозначения дискретного аргумента у функции с помощью нижнего индекса, например, yt вместо y(t).

Рассмотренные выше разности есть разности первого порядка. В численном анализе используются разности порядков выше первого: правые разности

5

Обыкновенным разностным уравнением порядка r называется уравнение

вида

Обыкновенное разностное уравнением порядка r можно представить как со-

отношение, связывающее yt и разности i yt или i yt вплоть до порядка r.

Решением разностного уравнения (10) называется функция yt , которая об-

ращает это уравнение в тождество.

В качестве примера рассмотрим паутинообразную модель равновесия. Пусть рынок какого-либо отдельного товара характеризуется следующими объема-

ми спроса и предложения: и . Для существования равновесия цена должна быть такой, чтобы товар на рынке был распродан,

или . Цена равновесия P и соответствующий объем покупок-

продаж, обозначаемый как X, задается уравнением: .

Предположим, что от времени производства товара до его попадания на рынок требуется один временной период. Производитель выпускает товар в период , цена которого в этот период равна . При этом объем про-

изводимого товара равен . Этот товар попадает на рынок в период .

Соответственно объем предложения на рынке в периоде будет , и величина должна установиться так, чтобы был куплен весь объем предложенного товара. Иными словами , и объем покупок-продаж характеризуются уравнением:

Итак, зная исходную цену с помощью уравнения (11) мы можем получить значения и . Затем, используя имеющуюся цену , аналогично получим

6

значения и т.д. В общем, изменение характеризуется разностным уравнением первого порядка (11).

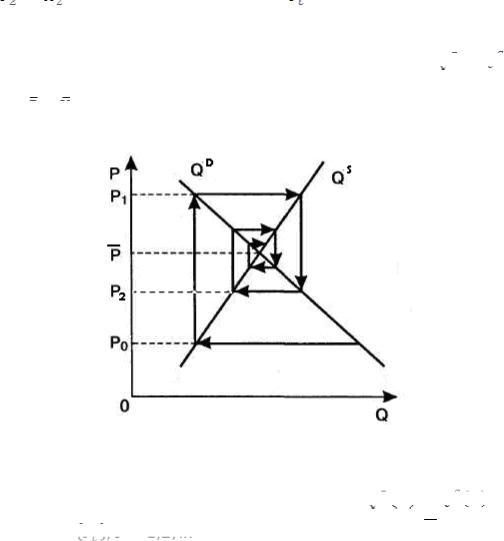
Решение можно проиллюстрировать графиком на рис.1, где и - соответственно графики спроса и предложения, а положение равновесия (со значениями и ) соответствует точке их пересечения.

Рис.1. Устойчивое равновесие спроса и предложения

На рис.1 видно, что для изображенных зависимостей и после-

довательность цен сходится к цене равновесия P.

7

2. Уравнения первого порядка, разрешенные относительно производной

Дифференциальное уравнение первого порядка, разрешенное относительно производной, записывается в виде

Функция f в (1) называется правой частью. В частном случае, когда правая часть зависит только от переменной x, решение уравнения (1) представляется в виде

y f (x)dx C ,

где C - произвольная постоянная, которая может быть определена, если известно значение решения в некоторой точке x0, y(x0) y0 . В таком случае

x

y y0 f (x)dx.

x0

В общем случае, когда правая часть есть функция переменных x и y , задача оказывается гораздо сложнее и для ее решения разрабатываются различные аналитические и численные методы.

Во многих задачах переменные x и y могут рассматриваться как рав-

ноправные. Поэтому, если для определения x и y требуется решить дифференциальное уравнение

8

то иногда имеет смысл для решения задачи рассматривать уравнение

легче интегрировать уравнение (3) чем уравнение (2). Если в некоторых точках одно из уравнений (2) или (3) теряет смысл, то в таких точках можно перейти к решению другого из этих уравнений.

Если оба уравнения (2) и (3) имеют смысл, то они эквивалентны. Действительно, если функция y y(x) является решением уравнения (2),

то обратная функция x x(y) является решением уравнения (3).

2.1. Геометрическое описание дифференциального уравнения Диффе-

ренциальное уравнение (1) в каждой точке x,y задает направление ка-

сательной к графику решения.

С геометрической точки зрения задача нахождения решений дифференциального уравнения (1) сводится к нахождению семейства кривых, у ко-

торых направления касательных совпадают с направлением поля, задаваемого этим дифференциальным уравнением. Графики решений дифференциального уравнения вида (1) называ-

ются интегральными кривыми.

Пример 1. На рис.1 изображены поле направлений и

интегральные кривые дифференциального

9

уравнения dydx x2 .

Рис.1. Поле направлений и интегральные кривые в примере 1

Рассмотрим линии уровня функции f x,y , т.е. линии, на которых функция f сохраняет постоянное значение. Очевидно, что на этих линиях касатель-

ные к интегральным кривым сохраняют постоянное направление. Такие линии называются изоклинами. В примере 1 изоклинами являются прямые, параллельные оси ординат.

Пример 2. Пусть дано дифференциальное уравнение

dy x2 y2 . Очевидно, dx

уравнения изоклин имеют вид:

x2 y2 r, где r- произволь-

ная постоянная, и представляют собой окружности радиуса r с центром в начале координат. На рис.2 изображены соответствующие по-

ле направлений и интегральные кривые. При этом хорошо видны изоклины в виде окружностей.

Рис. 2. Поле направлений и интегральные кривые в примере 2

2.2.Уравнения с разделяющимися переменными

10