5. Энергия системы электрических зарядов. Энергия электрического поля.

Энергия взаимодействия системы электрических зарядов

Электрические заряды взаимодействуют между собой и это взаимодействие можно характеризовать потенциальной энергией (мы будем ее называть энергий взаимодействия).

,

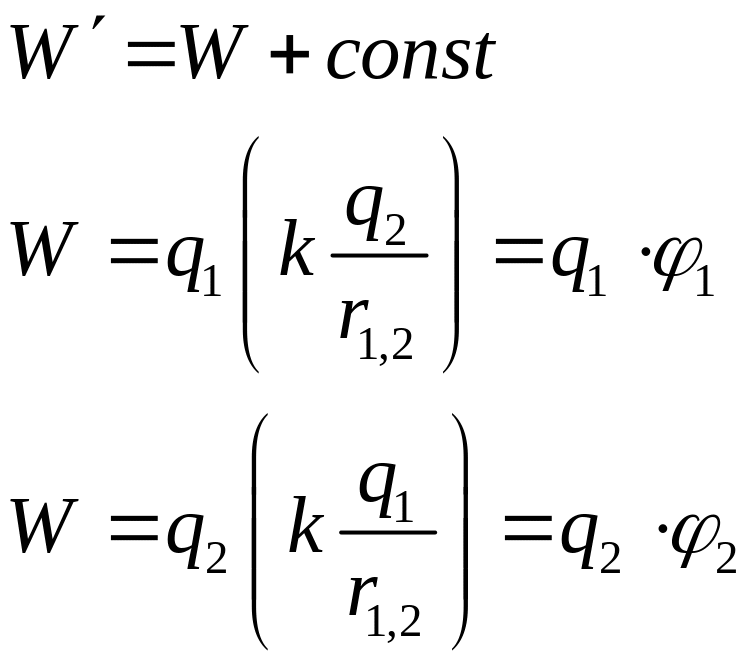
W – это энергия системы.

Для произвольной системы точечных зарядов сохраняется та же идея:

Пусть распределение зарядов непрерывное.

К

аждый dv – носитель точечного заряда.

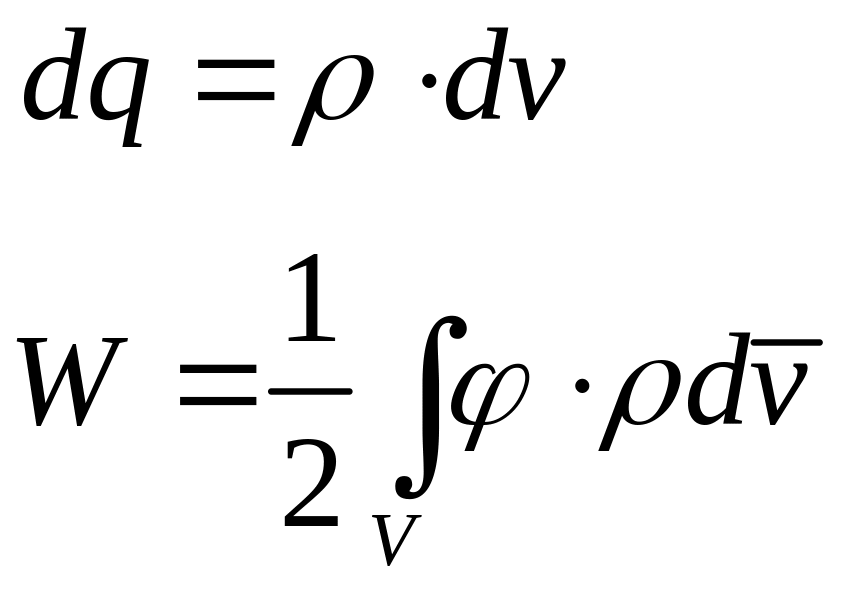
Энергия заряженного проводника.

Пример: проводник

Энергия заряженного конденсатора.

Энергия электрического поля.

Задача: выразить энергию через характеристику поля

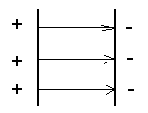
- плотность энергии электрического поля

Пример: неоднородное поле

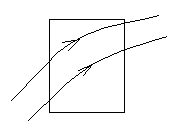
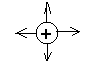
Рассмотрим систему из 2-х зарядов:

Проанализируем знаки полученных слагаемых:

; ; - из-за суперпозиции полей энергия взаимодействия. <0 (>0) из-за cos.

Таким образом исходная энергия системы 2-х зарядов > 0.

Складываются не энергия, а поля! Результат сложения полей определяет результирующую энергию системы. Когда рассматриваем взаимодействие зарядов, то рассматриваем только энергию их взаимодействия. Обычно ограничиваются только третьим слагаемым, т.е. - const=0.

6. Постоянный электрический ток и условия его существования. Законы Ома и Джоуля – Ленца в интегральной и дифференциальной формах.

Электрический ток – это направленный (упорядоченный) перенос электрических зарядов. В обычном состоянии вещества нет выделенного направления переноса.

Условия существования:

1. Наличие свободных зарядов.

2. Должно быть некоторое выделенное направление для движения зарядов. Его создает воздействие, которое бывает следующих видов: а) Кулоновское (электростатическое); б) Стороннее воздействие.

; . Носителями тока являются электроны, ионы. За направление тока принимают направление движения положительных зарядов.

Электрический ток через поверхность может быть неоднородным, и вводится понятие плотности тока: , где - элемент поверхности, перпендикулярно которой течет ток . Она показывает, какой заряд проходит за некоторое время через . и является функцией времени и координат.

Когда существует только электростатическое воздействие, то существование электрического тока невозможно. Необходимо обеспечить циркуляцию электрических зарядов – в какой-то области заряды должны двигаться против действия поля за счет источника сторонних сил – источника тока. Необходимо организовать замкнутую электрическую цепь. Она должна состоять из проводников, т.е. сам источник тока – проводник. В процессе движения зарядов сторонние силы будут совершать над ним работу. При отсутствии электрического поля носители тока (электроны, ионы) совершают хаотическое движение. Под действием силы, совершающей работу заряды начинают двигаться упорядоченно, т.е. возникает электрический ток. Следовательно между силой тока I и напряжением U должна быть некоторая связь. Закон Ома – частный случай этой связи для металлических проводников.

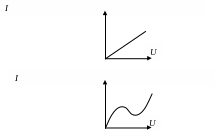
I(U) – вольтамперная характеристика проводника. Она может быть как линейной так и не линейной. Ом обнаружил линейную зависимость: I ~ U . Коэффициент пропорциональности зависит от проводника. , где R – сопротивление проводника. Зависимость может быть и не линейной. Например для вещества GaAs. При определенном напряжении U появляется переменный ток частотой 300 Гц.

В простом случае, если температура t постоянна, сопротивление зависит от проводника и его геометрии.

Р ассмотрим однородный проводник , где - удельное сопротивление проводника, зависит от вещества и температуры. В общем случае может зависеть от напряженности E электрического поля. Выражают в ом-метрах.

Интегральная форма закона Ома: , ,

1. Для однородного участка цепи (только электростатические силы)

2. Неоднородный участок цепи

, где - ЭДС.

Дифференциальная форма закона Ома:

Рассмотрим неоднородный проводник. Выделим в пределе

бесконечно малый цилиндр. Будем считать в его пределах всё

dS однородным. Тогда ток в нём .

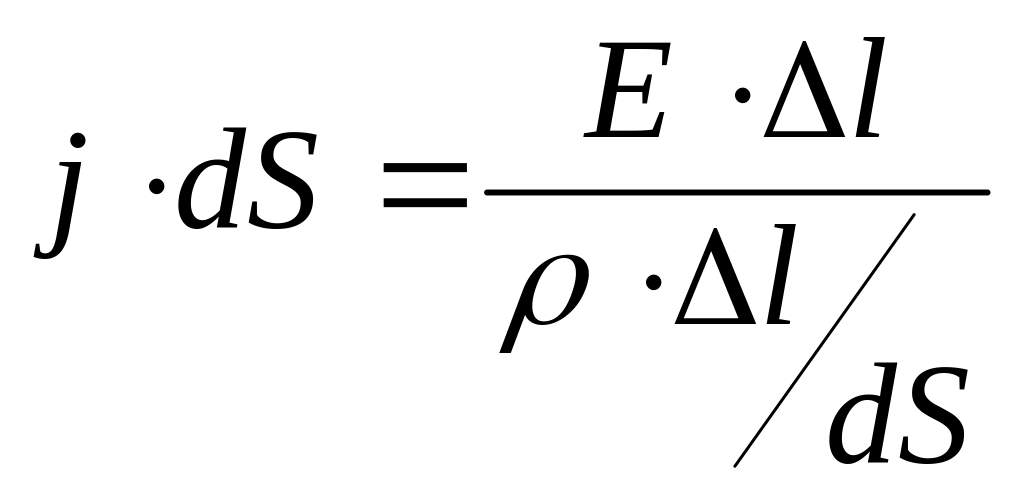, - Закон Ома в дифференциальной форме - связь между током и полем в локальной точке. - удельная электропроводность проводника. .

Закон Джоуля - Ленца:

Экспериментально установлено, что при протекании тока по проводнику в нём выделяется тепловая энергия: .

I Электростатические силы совершают над зарядами

работу:

. Работа электрического поля идет на перенос зарядов и сообщение им кинетической энергии, но в конечном счете переходит в тепловую энергию. Такая трансформация энергий связана со столкновением электронов с кристаллической решеткой.