3. Электрическое поле в диэлектрике. Условия на границе раздела 2-х диэлектриков.
Электрическое поле в диэлектрике. Интегральные теоремы для электрического поля в диэлектрике.
Д
иэлектрик
– вещество, в котором нет свободных
зарядов, только связанные. Диэлектрики
проводят ток в
раз хуже, чем проводники. Если диэлектрик
внести в электрическое поле, то это поле
и сам диэлектрик претерпевают существенные
изменения. Чтобы понять, почему это
происходит, нужно учесть, что в составе
атомов и молекул имеются положительно
заряженные ядра и отрицательные
электроны.
Появляется собственное поле связанных зарядов.
,
Результирующее поле в диэлектрике оказывается меньше, чем в вакууме.
E
- ?. Если знать, как распределены сторонние
и связанные заряды, то не составляет
труда посчитать
.
Но! Перераспределение связанных зарядов
тоже зависит от стороннего поля.
Вводится в рассмотрение новая величина, которая оказывается связанной с поляризационными зарядами.
,
,
,
- вектор электрического смещения.
- диэлектрическая
проницаемость
Физическим
смыслом обладает
,
а
особого физического смысла не несёт,
- вспомогательный вектор. Введение
вектора
позволяет находить
следующим образом:
.
Пример:
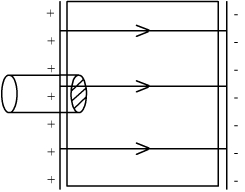
Помещаем диэлектрик (далее рассматриваем только линейные изотропные диэлектрики).
Диэлектрическая проницаемость вещества показывает во сколько раз напряжённость поля в диэлектрике меньше напряжённости поля в вакууме при таком же распределении сторонних зарядов.
Пример:
О
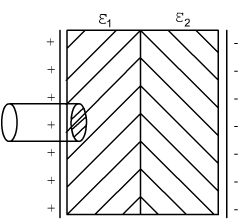снование
цилиндра перемещается.
Результат не зависит от положения S.
Для n
слоёв:
D=const
,
Напряжённость меняется.
Вектор связан только со сторонними зарядами, поэтому его линии начинаются и заканчиваются только на этих зарядах.
Вектор связан с любыми зарядами, и т. к. разные диэлектрики электризуются по-разному, то их собственные заряды будут иметь разные распределения, поляризованность в них будет разной, как результат – разное собственное поле и разная результирующая.
Силовые
линии (или просто – линии) вектора
.
Линии
.
Линии оказываются прерывистыми.
внутреннее собственное поле результирующее поле
Получается, что с удобнее иметь дело.
1.
2.
– наиболее перспективная
3.
4. Теорема о циркуляции .
- циркуляция вектора
.
Для
потенциального поля (электростатического):
- другая форма записи.
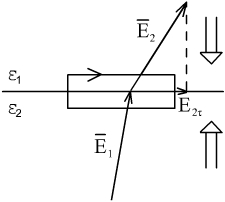
Условия на границе раздела двух диэлектриков.
Диэлектрики находятся в электрическом поле (в общем случае неоднородном). Вектор не обязательно перпендикулярен к поверхности.
Вектора направлены так же, как и соответствующие .
Граничное условие для :
1.
(знак зависит от
направления обхода).
- тангенциальная
составляющая
На границе раздела двух диэлектриков сохраняются тангенциальные составляющие вектора .
Тангенциальная составляющая вектора не сохраняется.
;
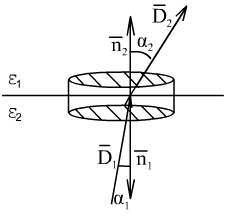
Граничное условие для :
2
.
(в общем случае)
Выбираем замкнутую поверхность в форме замкнутого цилиндра.
Вклад верхнего основания >0, а нижнего <0.
На границе раздела сохраняется нормальная составляющая вектора .
имеет разные нормальные составляющие.
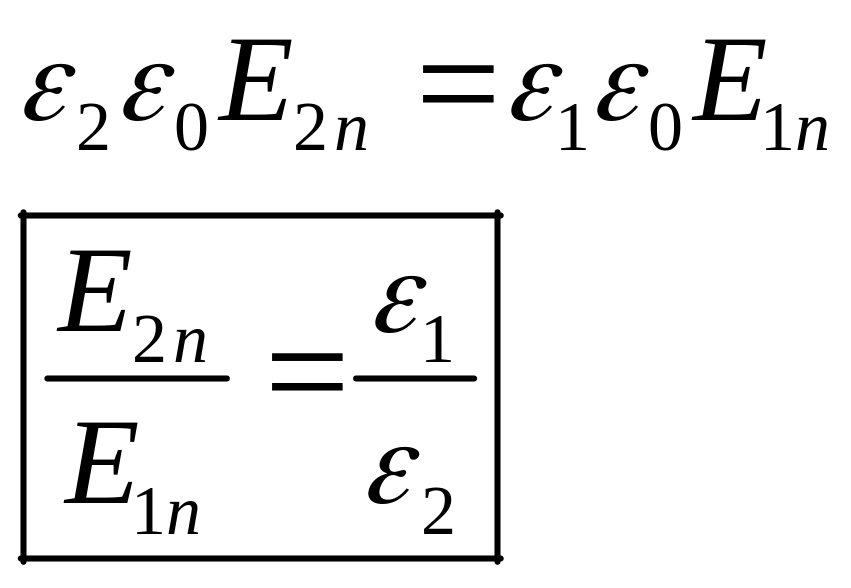
Зная вектор ( ) в одной среде, мы можем получить вектор ( ) в другой среде вблизи с границей раздела. С помощью этих условий можно рассчитывать поле в неоднородной среде, разбивая эту среду на тонкие слои.