
- •1. Электрическое поле в вакууме. Напряженность и потенциал. Принцип суперпозиции.
- •Элект. Заряды, их свойства и носители.
- •Различаются:
- •2. Теорема Гаусса и ее применение для расчета электрических полей.
- •3. Электрическое поле в диэлектрике. Условия на границе раздела 2-х диэлектриков.
- •4. Проводник в электрическом поле. Электрическая емкость проводника и системы проводников.
- •5. Энергия системы электрических зарядов. Энергия электрического поля.
- •6. Постоянный электрический ток и условия его существования. Законы Ома и Джоуля – Ленца в интегральной и дифференциальной формах.
- •7. Магнитное поле движущегося заряда. Закон Био-Савара-Лапласа и его применение для расчета магнитных полей
- •3Акон Био – Савара[-Лапласа]
- •8. Действие магнитного поля на движущиеся заряды и на проводники с током. Закон Ампера. Магнитный момент.
- •Работа по перемещению контура с током в магнитном поле.
- •9. Магнитное поле в веществе. Условия на границе раздела двух магнетиков.
- •10. Теорема о циркуляции индукции магнитного поля и ее применение для расчета магнитных полей.
- •11. Энергия системы проводников с током. Энергия магнитного поля.
- •12. Явление электромагнитной индукции. Эдс индукции и механизмы ее возникновения.
- •Контур движется в постоянном магнитном поле
- •Контур покоится в переменном магнитном поле.
- •13. Уравнения Максвелла.
- •14. Гармонические колебания и формы их представления. Сложение гармонических колебаний. Биения, фигуры Лиссажу.
- •15. Гармонический осциллятор. Энергия гармонического осциллятора.
- •16. Осциллятор с трением. Режимы движения. Затухающие колебания и их характеристики.
- •Дифференциальное уравнение осциллятора с трением
- •Затухающие колебания и их характеристики
- •17. Вынужденные колебания осциллятора. Резонанс. Импеданс колебательной системы.
- •Дифференциальное уравнение вынужденных колебаний
- •18. Волновые процессы и их разновидности. Волновое уравнение. Плоские гармонические волны.
- •Волновое уравнение.
- •Плоские гармонические волны и их характеристики.
- •19. Поперечные волны на непрерывной однородной струне. Волновое уравнение. Фазовая скорость волн. Импеданс струны.
- •20. Поперечные волны на границе раздела струн. Стоячие волны на струне.
- •21. Поперечные волны на дискретной струне. Явление дисперсии. Фазовая и групповая скорость волн.
- •22. Электромагнитные волны. Волновое уравнение. Плоские гармонические электромагнитные волны.
- •23. Импеданс среды для электромагнитных волн. Электромагнитные волны на границе раздела двух сред.
- •24. Интерференция волн от двух и многих когерентных источников.
- •25. Принцип Гюйгенса-Френеля. Дифракция света на щели.
- •26. Дифракция света на дифракционной решетке.
- •27. Поляризованный свет. Способы получения поляризованного света.
- •28. Тепловое излучение, его характеристики и закономерности. Подход Рэлея-Джинса. Гипотеза планка.
- •29. Фотоэффект и его закономерности. Формула Эйнштейна для фотоэффекта. Фотоны.
- •30. Гипотеза Луи де Бройля. Волновая функция. Принцип и соотношения неопределённостей. Гипотеза Луи де Бройля
- •Волновая функция
- •Принцип и соотношения неопределённостей
- •31. Уравнение Шредингера. Квантово-механическое описание свободных частиц.
- •32. Отражение частиц от потенциальной ступеньки. Туннельный эффект.
- •33. Частица в одномерной прямоугольной потенциальной яме. Квантование состояний.
- •34. Частица в двумерной потенциальной яме. Вырождение состояний.
- •Вырождение состояний.
- •35. Квантовый гармонический осциллятор.
- •36. Квантование момента импульса. Орбитальный и собственный момент импульса частицы.
Принцип и соотношения неопределённостей
С
1)
2)
Δx=nλ
,
=>
![]() =>
=>
![]() =>
=>
![]()
В общем случае пси может быть не синусоидой, тогда слагаемых ряда Фурье больше и Δp больше.
![]() точное -
точное -
![]() . ΔE – неопределённость
энергии состояния частицы, Δt
–время жизни состояния частицы.
. ΔE – неопределённость
энергии состояния частицы, Δt
–время жизни состояния частицы.
![]() .
.
31. Уравнение Шредингера. Квантово-механическое описание свободных частиц.
Основная идея Шрёдингера состоит в том, чтобы математическую аналогию между геометрической оптикой и классической механикой перенести на волновые свойства света и частиц.
Получим
уравнение Шрёдингера из выражения для
волновой функции свободного электрона
![]() .
Перепишем его в комплексной форме
.
Перепишем его в комплексной форме
![]() .
.
Используя
связи частоты с энергией, а волнового
числа с импульсом, получаем:
![]() .
.
В
общем случае
![]() – полная энергия частицы,
– полная энергия частицы,
![]() ,
,
![]() – кинетическая энергия и
– кинетическая энергия и
![]() –энергия взаимодействия.
–энергия взаимодействия.
Найдем
первую производную по
![]() и вторую по координате от ф-ции :
и вторую по координате от ф-ции :
![]() (1),
(1),
![]() (2).
(2).
Домножим
уравнение (1) на
![]() ,
а уравнение (2) на
,
а уравнение (2) на
![]() (таким образом множители в правых
частях будут иметь размерность энергии):
(таким образом множители в правых
частях будут иметь размерность энергии):
![]() ,
,
![]() .
.
Сложим полученные уравнения:
 .
.
Так
как
![]() ,
то последнее равенство перепишется в
виде
,
то последнее равенство перепишется в
виде
![]() .
.
Это
и есть уравнение Шрёдингера. Оно получено
для одной координаты
![]() .
Если его переписать для 3 координат
.
Если его переписать для 3 координат
![]() ,
то введя оператор Лапласа, окончательно
будем иметь
,
то введя оператор Лапласа, окончательно
будем иметь
![]() .
.
Уравнение Шрёдингера нельзя непосредственно вывести из фундаментальных законов классической физики. Уравнение Шрёдингера позволяет находить волновую функцию в произвольный момент времени. Для этого надо знать волновую ф-цию в фиксированный момент времени, массу частицы и энергию взаимодействия частицы с силовым полем. Найденная волновая ф-ция дает возможность рассчитать вероятность нахождения частицы в произвольной точке пространства для любого момента времени.
Основные свойства, которым должны удовлетворять волновые функции – решения уравнения Шрёдингера:
Волновая функция линейна, т.е. если
 …-
решения уравнения, то их линейная
комбинация
…-
решения уравнения, то их линейная
комбинация
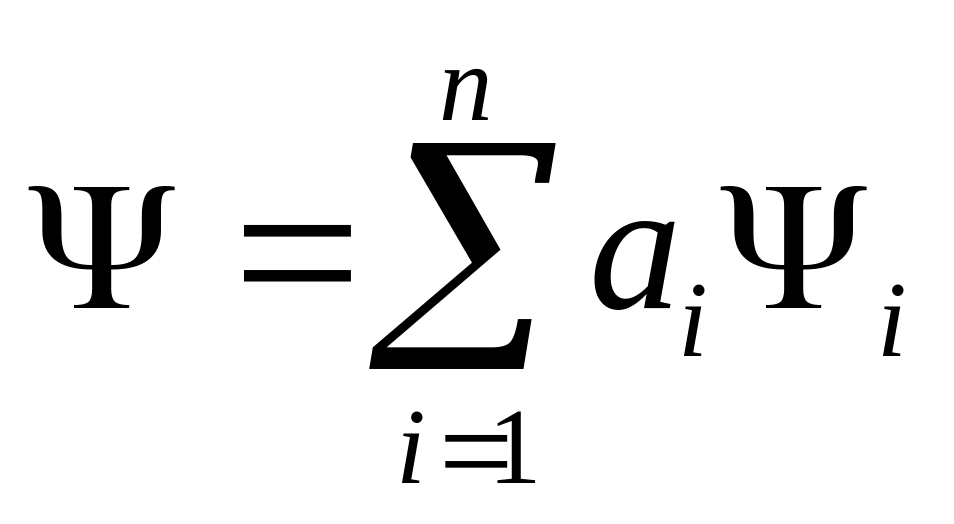 –
решение.
–
решение.Первые частные производные по координатам являются линейными
Волновая функция и её пространственные производные должны быть однозначными, конечными и непрерывными.
При стремлении к ∞ значение волновой функции должно стремиться к нулю.
Уравнение Шрёдингера для стационарных состояний.
Если силовое поле, в котором движется описываемая частица, стационарно, то потенциал его не зависит явно от времени, а функция имеет смысл потенциальной энергии и зависит только от координат . В этом случае волновую функцию можно представить как произведение двух. Одна функция зависит только от , другая – только от времени :
![]()
Подставим последнее выражение в уравнение Шрёдингера
![]() .
.
После
сокращения на временной множитель
![]() и некоторых элементарных преобразований
получим:
и некоторых элементарных преобразований
получим:
![]() (*).
(*).
Это
уравнение Шрёдингера для стационарных
состояний. В него входит только
координатная часть волновой ф-ции –![]() .
Если последняя будет найдена, то полная
волновая ф-ция находится домножением
координатной части на временной множитель
.
.
Если последняя будет найдена, то полная
волновая ф-ция находится домножением
координатной части на временной множитель
.
Поскольку вероятность определяется квадратом волновой ф-ции, а квадрат комплексной величины находится умножением на комплексно сопряженную, то имеет место следующее соотношение для стационарных волновых функций:
![]() .
.
Таким образом, чтобы найти волновую ф-цию для стационарных состояний, необходимо решить уравнение (*) и знать полную энергию .
Свободное движение частиц.
Во время свободного
движения квантовой частицы никакие
силы на нее не действуют и можно ее
потенциальную энергию равной нулю.
Пусть движение частицы происходит в
направлении
,
тогда (*) принимает вид:
![]() .
.
Частным
решением этого уравнения является ф-ции
вида
![]() ,
где
,
где
![]() и
– константы. Если подставить искомое
решение в само уравнение, то мы получим
связь энергии частицы
и величины
:
и
– константы. Если подставить искомое
решение в само уравнение, то мы получим
связь энергии частицы
и величины
:![]()
Полная
волновая функция с учетом зависимости
от времени для свободной частицы имеет
вид
![]() .
Это плоская монохроматическая волна с
частотой
.
Это плоская монохроматическая волна с
частотой
![]() и волновым числом
.
Так как
и волновым числом
.
Так как
![]() ,
а
,
а
![]() ,
то
,
то
![]() .
.
Мы
получили обычное выражение, связывающее
кинетическую энергию и импульс
нерелятивистской частицы. Величины
и
![]() такой частицы ничем не ограничены, те
свободная квантовая частица может иметь
любое значение энергии и импульса.
Вероятность обнаружения частицы в
интервале координат
такой частицы ничем не ограничены, те
свободная квантовая частица может иметь
любое значение энергии и импульса.
Вероятность обнаружения частицы в
интервале координат
![]() определяется соотношением
определяется соотношением
![]() .
.
Величину,
стоящую перед
![]() ,
будем называть плотностью вероятности
,
будем называть плотностью вероятности
![]() .
.
Это означает равную вероятность обнаружения свободной частицы в любой точке направления , т.е. область движения вдоль « » у свободной частицы ничем не ограничена. Энергия частицы может быть любой, начиная с нуля, так как из уравнения Шрёдингера нет никаких ограничений на величину .
