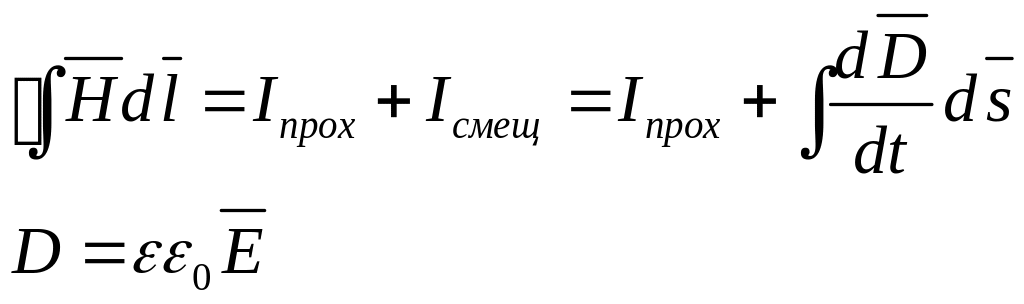- •1. Электрическое поле в вакууме. Напряженность и потенциал. Принцип суперпозиции.
- •Элект. Заряды, их свойства и носители.
- •Различаются:
- •2. Теорема Гаусса и ее применение для расчета электрических полей.
- •3. Электрическое поле в диэлектрике. Условия на границе раздела 2-х диэлектриков.
- •4. Проводник в электрическом поле. Электрическая емкость проводника и системы проводников.
- •5. Энергия системы электрических зарядов. Энергия электрического поля.
- •6. Постоянный электрический ток и условия его существования. Законы Ома и Джоуля – Ленца в интегральной и дифференциальной формах.
- •7. Магнитное поле движущегося заряда. Закон Био-Савара-Лапласа и его применение для расчета магнитных полей
- •3Акон Био – Савара[-Лапласа]
- •8. Действие магнитного поля на движущиеся заряды и на проводники с током. Закон Ампера. Магнитный момент.
- •Работа по перемещению контура с током в магнитном поле.
- •9. Магнитное поле в веществе. Условия на границе раздела двух магнетиков.
- •10. Теорема о циркуляции индукции магнитного поля и ее применение для расчета магнитных полей.
- •11. Энергия системы проводников с током. Энергия магнитного поля.
- •12. Явление электромагнитной индукции. Эдс индукции и механизмы ее возникновения.
- •Контур движется в постоянном магнитном поле
- •Контур покоится в переменном магнитном поле.
- •13. Уравнения Максвелла.
- •14. Гармонические колебания и формы их представления. Сложение гармонических колебаний. Биения, фигуры Лиссажу.
- •15. Гармонический осциллятор. Энергия гармонического осциллятора.
- •16. Осциллятор с трением. Режимы движения. Затухающие колебания и их характеристики.
- •Дифференциальное уравнение осциллятора с трением
- •Затухающие колебания и их характеристики
- •17. Вынужденные колебания осциллятора. Резонанс. Импеданс колебательной системы.
- •Дифференциальное уравнение вынужденных колебаний
- •18. Волновые процессы и их разновидности. Волновое уравнение. Плоские гармонические волны.
- •Волновое уравнение.
- •Плоские гармонические волны и их характеристики.
- •19. Поперечные волны на непрерывной однородной струне. Волновое уравнение. Фазовая скорость волн. Импеданс струны.
- •20. Поперечные волны на границе раздела струн. Стоячие волны на струне.
- •21. Поперечные волны на дискретной струне. Явление дисперсии. Фазовая и групповая скорость волн.
- •22. Электромагнитные волны. Волновое уравнение. Плоские гармонические электромагнитные волны.
- •23. Импеданс среды для электромагнитных волн. Электромагнитные волны на границе раздела двух сред.
- •24. Интерференция волн от двух и многих когерентных источников.
- •25. Принцип Гюйгенса-Френеля. Дифракция света на щели.
- •26. Дифракция света на дифракционной решетке.
- •27. Поляризованный свет. Способы получения поляризованного света.
- •28. Тепловое излучение, его характеристики и закономерности. Подход Рэлея-Джинса. Гипотеза планка.
- •29. Фотоэффект и его закономерности. Формула Эйнштейна для фотоэффекта. Фотоны.
- •30. Гипотеза Луи де Бройля. Волновая функция. Принцип и соотношения неопределённостей. Гипотеза Луи де Бройля
- •Волновая функция
- •Принцип и соотношения неопределённостей
- •31. Уравнение Шредингера. Квантово-механическое описание свободных частиц.
- •32. Отражение частиц от потенциальной ступеньки. Туннельный эффект.
- •33. Частица в одномерной прямоугольной потенциальной яме. Квантование состояний.
- •34. Частица в двумерной потенциальной яме. Вырождение состояний.
- •Вырождение состояний.
- •35. Квантовый гармонический осциллятор.
- •36. Квантование момента импульса. Орбитальный и собственный момент импульса частицы.
21. Поперечные волны на дискретной струне. Явление дисперсии. Фазовая и групповая скорость волн.
В ещество,
в том числе и струна, это среда дискретная,
в конечном счете она состоит из атомов.
Если струна непрерывна, то на ней могут
существовать волны любой длины.
ещество,
в том числе и струна, это среда дискретная,
в конечном счете она состоит из атомов.
Если струна непрерывна, то на ней могут
существовать волны любой длины.
Масса шариков одинакова и располагаются они одинаково дискретная струна характеризуется двумя параметрами: массой и периодом.
m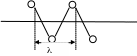 in=2a
in=2a
гармоническая волна
Если среда дискретная, то в ней наблюдается дисперсия волн, которая выражается в том, что w(k)!=Vф. Vф!=const, k – не линейная функция.
П рименяем
второй закон Ньютона для участка струны.
рименяем
второй закон Ньютона для участка струны.
![]()

![]() - (*) волновое
уравнение для дискретной струны
- (*) волновое
уравнение для дискретной струны
имеет дифференционно-разностную природу.
yn(t)=Aei(wt-kx)=Aei(wt-kna)
![]() (**)
(**)
сделав
подстановку (**) в (*), получили:
![]()
![]()
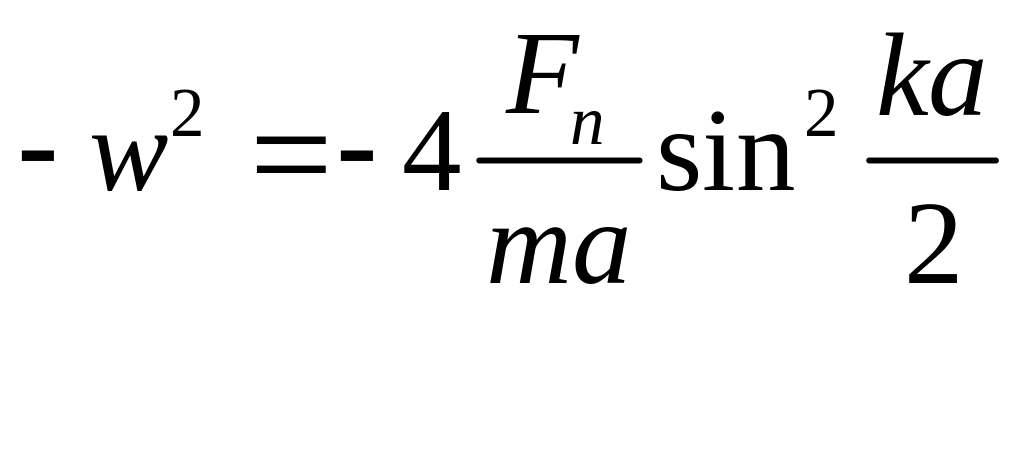
![]() на величину
циклической частоты накладывается
ограничение.
на величину
циклической частоты накладывается
ограничение.

![]()
![]()
![]()
![]()
Максимальное значение частоты представляет собой собственную частоту противофазных колебаний соответствующих самой
маленькой длине волны.
![]()
 ,
,
![]()
1)Низкие частоты: w->0, k->0
![]() фазовая
скорость для непрерывной струны, где
фазовая
скорость для непрерывной струны, где
![]() .
.
Изломы не играют роли (системы не ощущает своей дискретности)
![]() непрерывной струны.
непрерывной струны.
2) высокие частоты : w-> , k->
![]() низкие частоты.
Волновой
пакет при такой волне будет деформироваться.
Волны с низкой частотой будут
распространяться с «обычной » скоростью.
Волны с высокой частотой будут
распространяться более медленно.
низкие частоты.
Волновой
пакет при такой волне будет деформироваться.
Волны с низкой частотой будут
распространяться с «обычной » скоростью.
Волны с высокой частотой будут
распространяться более медленно.
![]() переноса
энергии нет.
стоячая волна.
переноса
энергии нет.
стоячая волна.
Если система дискретна, она ведет себя как дискретная струна. Такие системы характеризует дисперсия.
22. Электромагнитные волны. Волновое уравнение. Плоские гармонические электромагнитные волны.

Электромагнитные волны представляют собой распространяющиеся в пространстве колебания электромагнитного поля. Источник – движущиеся заряды. В качестве исходного уравнения будем использовать уравнение Максвелла, в которое входит временное изменение полей.
Электромагнитное
поле характеризуется векторами
![]() ,
а физическим смыслом обладают векторы
,
а физическим смыслом обладают векторы
![]() .
.
Получим волновое уравнение для случая плоских волн.

![]()
![]()
За счет этого поля появляется магнитное поле.
Уменьшим ширину по x прямоугольника в плоскости xy.
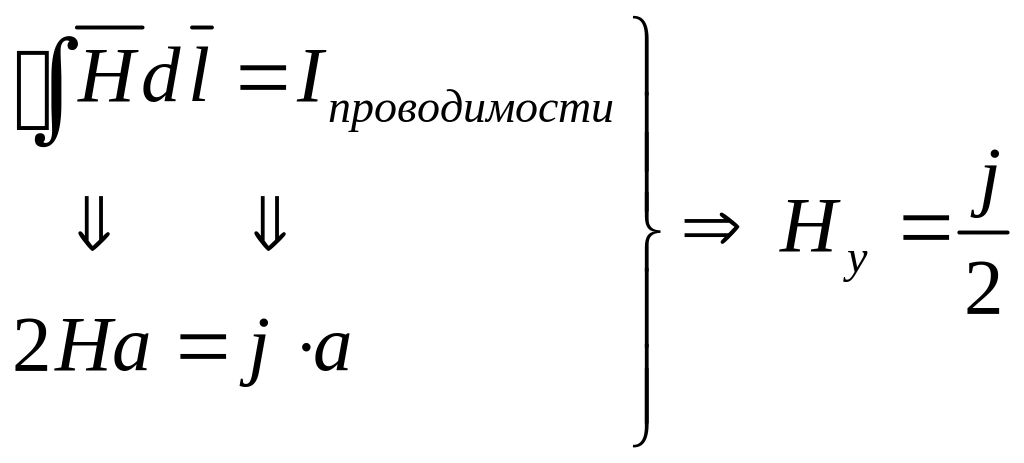 - проекция H
на ось y.
- проекция H
на ось y.
![]()
Силовые линии
должны быть перпендикулярны вектору
![]()
Пусть в пространстве непроводящая среда, т.е. удельная проводимость = 0.
Среду
будем характеризовать
![]() .
.
![]() .
Изменение магнитного поля
возникает
электрическое поле.
.
Изменение магнитного поля
возникает
электрическое поле.
![]() .
.
а - длина


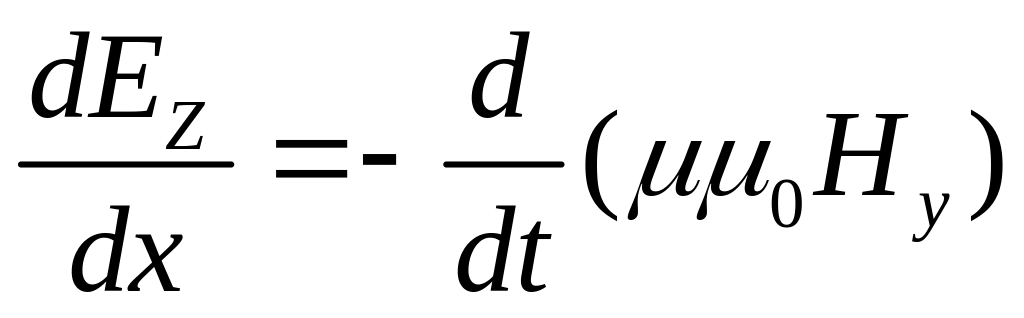 - связь меняющегося
магнитного поля и электрического поля.
- связь меняющегося
магнитного поля и электрического поля.

- положение
направление обхода контура (по Буравчику)
 - связи между
меняющимися полями
- связи между
меняющимися полями
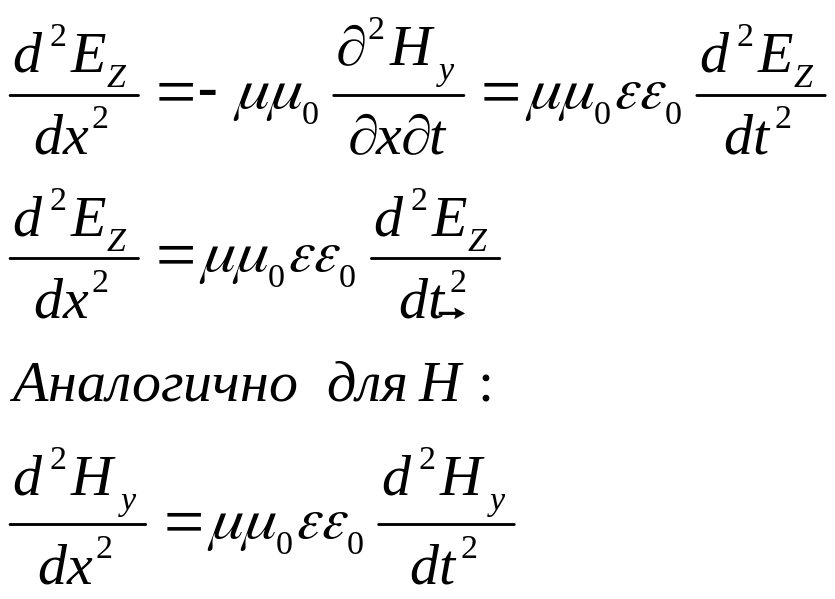 - волновые уравнения
- волновые уравнения
В среде будут
распространяться электромагнитные
волны, в них будут присутствовать
![]() .
Волна носит электромагнитную
природу.
.
Волна носит электромагнитную
природу.
Плоские электромагнитные волны и их структура.
![]() - описывает
возмущение магнитной составляющей
вблизи плоскости. Возмущение будет
распространятся в пространстве с
- описывает
возмущение магнитной составляющей
вблизи плоскости. Возмущение будет
распространятся в пространстве с

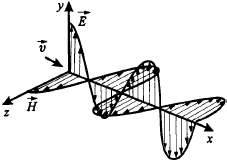
![]() Фазы у
Фазы у
![]() и
и
![]() одинаковые.
одинаковые.
В
вакууме
![]() и, тогда,
и, тогда,
![]()