Московский Государственный Технический Университет

им. Н. Э. Баумана

Калужский филиал

Н. Ф. Врублевский расчет электрических цепей синусоидального тока

Методические указания

Калуга

Издательство МГТУ им. Н.Э. Баумана

2012

УДК.____.___

ББК.____.___

В-____

Методические указания «Расчет электрических цепей синусоидального тока» по курсу «Электротехника и электроника», издаются в соответствии с учебным планом специальностей №151001 «Технология машиностроения», №151002 «Металлообрабатывающие станки и комплексы», №151003 «Инструментальные системы машиностроительных производств», №150202 «Оборудование и технология сварочного производства», №101400 «Газотурбинные, паротурбинные установки и двигатели», №121100 «Гидравлические машины, гидроприводы и гидропневмоавтоматика».

Методические указания рассмотрены и одобрены:

Кафедрой ЭИУ7 – КФ «Электротехника»

протокол №___ от «___»___________20___г.

Зав.кафедрой ЭИУ7 – КФ ___________Д. В. Мельников

Методической комиссией факультета ЭИУК

протокол №___ от «___»___________20___г.

Председатель методической комиссии ф-та ЭИУК _____М. Ю. Адкин

Методической комиссией Калужского филиала

протокол №___ от «___»___________20___г.

Председатель методической комиссии ___________А. Н. Малышев

Автор:

к.т.н., доцент кафедры ЭИУ7 – КФ ____________Н. Ф. Врублевский

В данном методическом пособии содержатся теоретический материал и пример расчёта, необходимые для самостоятельного выполнения домашнего задания «Расчет электрических цепей синусоидального тока» по курсу «Электротехника и электроника».

Данные методические указания могут быть использованы при проведении практических занятий по курсу «Электротехника и электроника».

ВВЕДЕНИЕ

Теория электрических цепей синусоидального тока – один из наиболее трудных для усвоения разделов электротехники. Математическим аппаратом теории является алгебра комплексных чисел. Студент должен научиться свободно оперировать комплексными числами, уметь переходить от одной формы их записи к другой.

Расчёт цепей синусоидального тока возможен только при твёрдом знании основных расчётных формул, поэтому их усвоению следует уделить должное внимание.

Содержание курса лекций и настоящие методические материалы дают достаточную информацию для самостоятельного выполнения предусмотренного учебным планом домашнего задания.

1. Комплексный метод расчёта синусоидального тока

Комплексный метод основывается на исчислении комплексных чисел и соответствующей замене мгновенных значений синусоидальных величин комплексами. При этом осуществляется переход от интегродифференциальных уравнений, составленных для рассматриваемой цепи по законам Ома и Кирхгофа, к алгебраическим уравнениям для комплексных величин. Полученная система алгебраических уравнений решается относительно неизвестных комплексных параметров, например комплексов токов. Затем осуществляется переход от комплексных величин к соответствующим им мгновенным значениям. Таким образом, сложная проблема решения интегрдифференциальных уравнений заменяется более простой задачей решения алгебраических уравнений, а расчет линейных электрических схем гармонического тока в установившемся режиме становится аналогичен расчету электрических схем постоянного тока. Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с возможностью проведения точных аналитических расчетов цепей и поэтому наиболее часто применяется на практике.

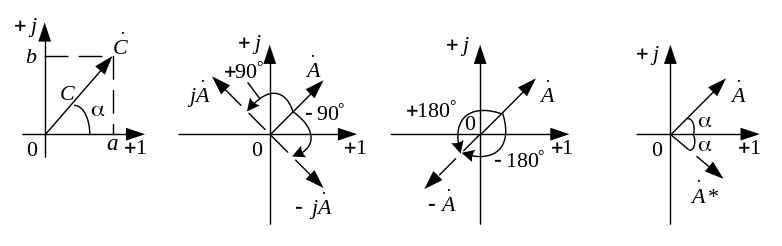а) б) в) г)

Рис. 1. Представление комплексного числа в виде вектора

Комплексным числом называют сумму действительного и мнимого чисел, например , где а и b - действительные числа; - мнимая единица.

Число является действительным числом, а число – мнимым. Мнимая единица обладает следующим свойством:

; и т.д.

Комплексное число можно представить в виде вектора на комплексной плоскости (рис. 1, а), ось абсцисс которой называется действительной осью, а ось ординат – мнимой.

Существует показательная, тригонометрическая и алгебраическая формы аналитической записи комплексного числа:

.

Модуль комплексного числа равен корню квадратному из суммы квадратов действительной и мнимой частей:

,

а аргумент комплексного числа (угол наклона вектора к мнимой оси на комплексной плоскости) равен арктангенсу отношения мнимой части к действительной:

.

Если ,то .

Показательная и алгебраическая формы являются основными, а тригонометрическая вспомогательной, обеспечивающей переход от одной основной формы к другой. Для удобства перехода используют формулу Эйлера:

.

Умножение комплекса на означает поворот соответствующего ему вектора на комплексной плоскости на угол против часовой стрелки (рис. 1, б):

Пользуясь формулой Эйлера, получим

.

Следствие. Умножение комплекса на соответствует повороту на угол .

Умножение комплекса на означает поворот соответствующего ему вектора на комплексной плоскости на угол (направление поворота безразлично) (рис. 1, в):

Пользуясь формулой Эйлера, имеем

.

Умножение комплекса на сопряженный комплекс (рис. 1, г).

Если , то сопряженным ему называется комплекс . Следовательно, .

Следует отметить, что при операциях сложения (вычитания) комплексных чисел необходимо использовать алгебраическую форму записи для слагаемых. Соответственно при операции умножения комплексных чисел целесообразно применять показательную форму:

.

Синусоидальные функции переводят в изображающие их комплексы следующим образом:

Для перехода от комплексов к соответствующим мгновенным значениям необходимо выполнить следующие операции:

При расчете цепей переменного тока также возникает необходимость описывать комплексы падения напряжения на элементах , и .

Для резистивного элемента

,

следовательно,

.

Для катушки индуктивности имеем

,

а для конденсатора

.

Для соответствующих комплексов и получаем:

,

,

где и - реактивные сопротивления индуктивности и емкости соответственно.