3. Практическая часть

Постановка задачи.

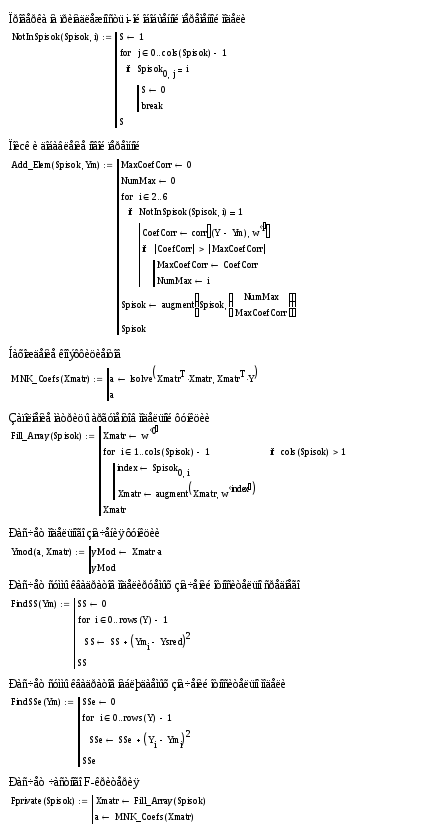
Проведены 23 наблюдения переменных x1 и Y=ln(x3). Необходимо выбрать оптимальную модель Ym(x1) линейного вида с использованием заданных тригонометрических базисных функций и найти коэффициенты модели. Включение и исключение модели определяется F-критерием. Используется шаговый метод отбора.

4. Выводы

На основании полученных результатов, мы можем сделать вывод о том, что найденная модельная функция достаточно точно описывает неизвестную зависимость. Коэффициент множественной регрессии R2 = 0.989, дисперсия ошибки моделированияSe2 = 9,60810^-4,F-критерий = 270,298, говорят о том, что достоверность полученных выходных данных (т.е. значений модельной функции) актуальна.

.

Используемая литература:

1. Нехаев И.Н. Решение задач вычислительной математики с примерами решения в пакете «MathCad»: Учебное пособие.-Йокар-Ола: МарГТУ, 2004.

2. Применение математических методов и ЭВМ: Практикум: Учеб. пособие для вузов.

3. Мэтьюз Джон, Финк Куртис. Численные методы. Использование Matlab. М.:Изд.дом Вильямс, 2001.

2