Оценка математического ожидания по неравноточным наблюдениям

Ранее мы предполагали, что все наши наблюдения равноточны, т.е. имеют одинаковую дисперсию. Однако на практике встречаются и ситуации неравноточных наблюдений. А именно, пусть для независимых наблюдений х₁,х₂,...,х_n выполнено условие:

Mx₁= Mx₂=… =Mx_n=a; Dx₁= , Dx₂= , …, Dx_n= .

Требуется найти наилучшую оценку для математического ожидания.

Наилучшую в статистическом смысле оценку (в смысле несмещенности и эффективности) будем искать в классе линейных оценок.

Классом линейных несмещенных оценок параметра  называется класс оценок вида =c₁x₁+c₂x₂+…+ c_nx_n , для которых Числовые коэффициенты c₁, c₂, … c_n называются весами наблюдений.

Из требования несмещенности оценки следует, что должно выполняться равенство

.

Следовательно, оценка будет несмещенной, если .

Чтобы получить эффективную оценку (в классе линейных несмещенных оценок), надо минимизировать дисперсию оценки

,

то есть определить коэффициенты с_i так, чтобы дисперсия была минимальна, но при условии, что Дисперсия вычисляется при условии, что случайные величины x_i независимы.

Задача свелась к нахождению таких коэффициентов с_i, при которых функция имеет минимум при условии . Это задача на условный экстремум. Функция Лагранжа имеет вид L(с)=φ(с)-g(с). Для определения коэффициентов приравниваем нулю производные:

  

Из этих условий получаются значения для коэффициентов: .

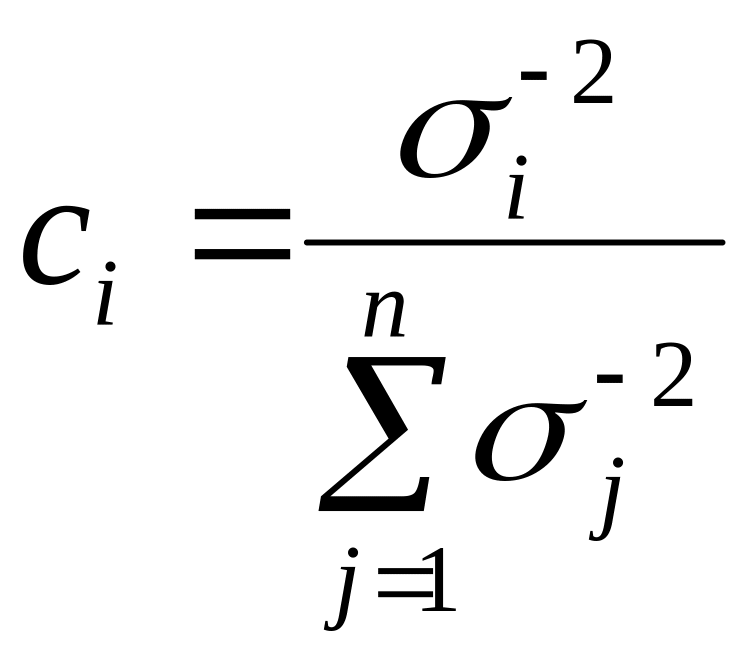Таким образом, веса наблюдений должны быть обратно пропорциональны их дисперсиям (менее точные наблюдения, имеющие большую дисперсию, входят с меньшим весом, более точные – с большим). В результате, эффективной оценкой математического ожидания оказывается средневзвешенное значение, имеющее вид

,

с дисперсией, равной .

Проверим состоятельность полученной оценки математического ожидания по неравноточным наблюдениям. Учитывая независимость наблюдений найдем дисперсию оценки при полученных значениях коэффициентов:

.

Если при , то дисперсия и в силу теоремы 7.3.4 оценка − состоятельная оценка математического ожидания.

Если дисперсии наблюдений равны (т.е. наблюдения равноточные), то с_i = 1/n, для любого i=1,2,…,n, и , т.е. среднее арифметическое выборки является эффективной оценкой математического ожидания в классе линейных несмещенных оценок при любом распределении, имеющем конечные математическое ожидание и дисперсию.

Если равноточные наблюдения производятся для k независимых выборок из одной генеральной совокупности, то дисперсия выборочного среднего по i-ой из них оказывается обратно пропорциональна объему выборки n_i. Отсюда получаем c_i=n_i/n, где n – сумма объемов всех выборок, и наилучшей оценкой математического ожидания является .

Задача Двое исследователей провели независимые выборочные обследования доходов населения. Первый определил средний годовой доход 3000 у.е. cо средним квадратическим отклонением ₁=100 у.е., второй – 2900 у.е. с ₂=50 у.е. Построить наиболее точную оценку среднего годового дохода и найти ее среднее квадратическое отклонение.

Решение. Вычислим обратные квадраты дисперсий: =0,0001; =0,0004. Их сумма равна 0,0005. Отсюда c₁=1/5, c₂=4/5. Получаем =(1/5)3000+(4/5)2900=2920 (у.е.), дисперсия =1/0,0005=2000, среднее квадратическое отклонение 44,72 (у.е.).