Эффективность оценок. Неравенство Рао-Фреше-Крамера

Для одних и тех же параметров распределения существует бесконечно много различных несмещенных и состоятельных оценок. Поэтому важной задачей является сравнение их между собой и поиск наилучшей среди них. Естественным критерием такого поиска является дисперсия, как мера разброса значений случайной величины вокруг его среднего значения, и наилучшей оценкой является оценка с минимальной дисперсией. Однако для смещенной оценки дисперсия служит мерой близости не к оцениваемому параметру , а к математическому ожиданию этой же оценки . Поэтому естественно искать наилучшие оценки с наименьшей дисперсией только среди несмещенных оценок.

Получая ту или иную оценку, мы должны иметь возможность определить, обладает ли она минимальной дисперсией из всех возможных, или нет. С этой целью вводится понятие эффективности оценки и используется неравенство Рао-Фреше-Крамера.

Информацией Фишера о неизвестном параметре , содержащейся в одном из независимых наблюдений случайной величины , называется величина

,

где в качестве берется либо плотность в точке x (для непрерывных случайных величин), либо вероятность принять значение x (для дискретных случайных величин). Говорят, что величина определяет количество информации Фишера.

Теорема Рао-Фреше-Крамера).

Пусть задана несмещенная оценка , построенная по выборке х₁,x₂,…,x_n, а функция плотности f(x,) удовлетворяет следующим условиям регулярности:

1) область G_n={x: f(x,)>0} не зависит от параметра ;

2) в тождествах

и

допустимо дифференцирование по  под знаком интеграла;

3) информация Фишера I() конечна и положительна.

Тогда выполняется неравенство (Рао-Фреше-Крамера):

.

Доказательство. Пусть – несмещенная оценка параметра , т.е.

,

где Х = (х₁,x₂,…,x_n) и f(X,) - плотность распределения, так что .

Дифференцируя по  равенства (7.4.1) и (7.4.2), получим

и .

Умножим второе равенство на  и вычтем его из первого

По условию на множестве G_n плотность f(X,) > 0, поэтому можно записать, что .

Подставим полученное выражение в равенство (7.4.3) и используя неравенство Коши-Буняковского находим

или

Учитывая независимость и одинаковый закон распределения наблюдений x₁,x₂,…,x_n, можно записать, что

Подставляя это выражение в последнее неравенство, окончательно получаем утверждение теоремы D  .

Замечание 1. Теорема верна и в дискретном случае, если в условии 2) заменить интегралы на суммы (по всем возможным значениям случайной величины).

Замечание 2. Если оценка является линейной функцией выборочного среднего, т.е. , то первое тождество из условия 2) эквивалентно более простому: .

Замечание 3. Информацию Фишера можно также представить в виде:

и .

Обозначим правую часть неравенства Рао-Фреше-Крамера через _n=1/nI(). Эта величина является нижней гранью всех возможных дисперсий оценок.

Эффективностью несмещенной оценки называется отношение минимально возможного значения дисперсии оценки в классе всех несмещенных оценок параметра  к дисперсии рассматриваемой оценки:

.

Из определения следует, что эффективность любой несмещенной оценки удовлетворяет неравенству 0 1, и чем ближе она к единице, тем лучше оценка.

Несмещенная оценка называется эффективной, если =1.

Асимптотической эффективностью оценки называется предел , если он существует. Оценку называют асимптотически эффективной, если =1.

Кроме того, для асимптотически нормальных оценок понятие асимптотической эффективности иногда трактуется более широко. А именно, для асимптотически нормальной оценки при n, полагают .

Задача Доказать, что выборочное среднее является эффективной оценкой математического ожидания нормального распределения, когда дисперсия известна.

Решение. Выпишем функцию плотности для нормального распределения:

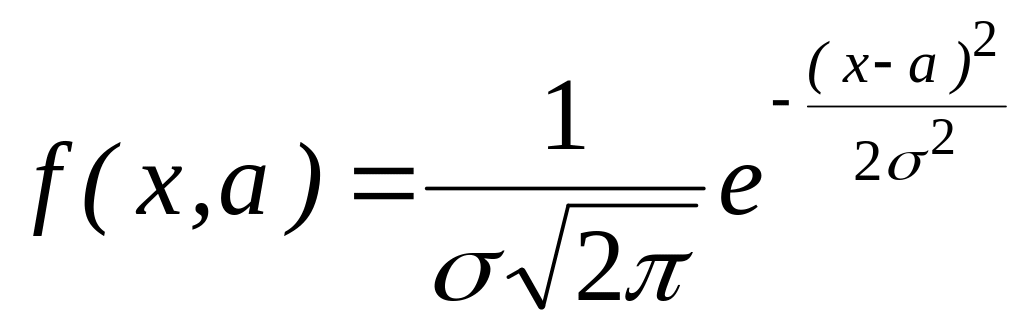
Прологарифмировав ее, получим: , при этом производная будет равна

Отсюда найдем информацию Фишера:

Получаем значение . С другой стороны, , так что .

Таким образом, оценка является эффективной. Из доказанного следует, что чем больше дисперсия нормальной случайной величины, тем меньше информации о значении математического ожидания этой величины заключено в одном наблюдении.

Задача. Доказать, что относительная частота успеха в качестве оценки неизвестной вероятности θ в схеме Бернулли является эффективной оценкой.

Решение. Оценкой неизвестной вероятности является относительная частота успеха , где х_i – успех (1) или неудача (0) в i-ом испытании. Эта оценка несмещенная, так как Дисперсия оценки имеет вид

.

Найдем информацию Фишера, причем в данном случае наблюдаемая величина принимает всего два значения: 0 и 1 с вероятностями P(0;)=1 и Р(1;)=.

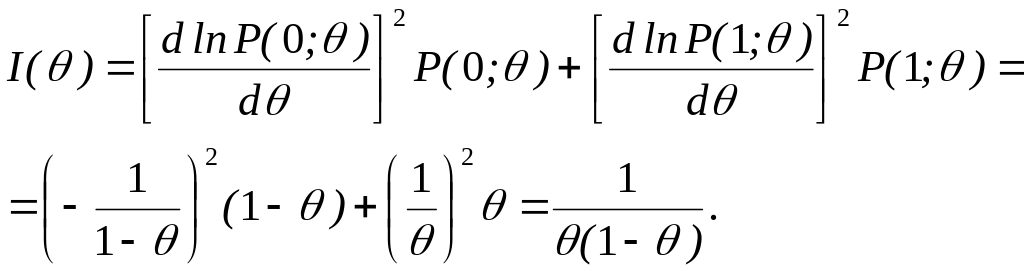
Таким образом, .

Задача. Пусть выборка x₁, x₂, ..., x_n произведена из генеральной совокупности с равномерным распределением на отрезке [0, ]. Проверить на эффективность оценку для неизвестного параметра .

Решение. Функция распределения F_max(x) максимума x_max задается формулой:

на отрезке 0х. Отсюда получаем

.

Значит, оценка несмещенная. Найдем дисперсию этой оценки:

Видно, что дисперсия оценки при n убывает как . Такая оценка оказалась лучше эффективной, поскольку дисперсия эффективной оценки имеет порядок убывания только . Разгадка парадокса в том, что для данного семейства распределений не выполнены условия теоремы Рао-Фреше-Крамера. А именно, область значений случайной величины зависит от параметра . Подобные оценки называют сверхэффективными.