2.5. Центр тяжести Координаты центра тяжести тела определяются по фор­мулам

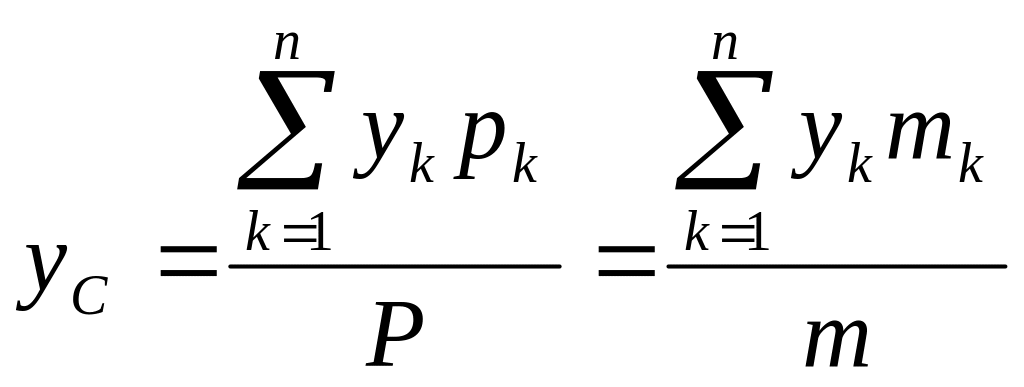; ; . (71)

Суммы, стоящие в числителях, называют стати­ческими моментами веса (массы) относительно плоскостей уОz, хОz, хОу соответственно.

Если тело однородно, то координаты его центра тяже­сти определяют по формулам

; ; . (72)

Координаты центра тяжести тонких однородных поверх­ностей (имеющих постоянный вес единицы площади) опре­деляют по формулам

; ; . (73)

Координаты центра тяжести пластины (оси Ох, Оу рас­положены в плоскости пластины):

; , (74)

где ; - статические моменты площади относительно осей Ох и Оу.

Аналогичные формулы применяют для определения координат центров тяжести тонких однородных стержней (имеющих постоянный вес единицы длины).

В формулах (72), (73) v_k, s_k - объемы и площади тех частей, на которые разбиваются тела (поверхности) слож­ной формы; M_k(x_k, у_k, z_k) - центры тяжести этих частей.

При нахождении центра тяжести тела (фигуры) с отвер­стиями можно применять формулы (71), (72), (73), считая веса, объемы или площади, соответствующие вырезанным частям, отрицательными. Для криволиней-ных тел (фигур), разбиваемых на бесконечно малые элементы, суммы в выра­жениях для статических моментов и масс (объемов, пло­щадей) заменяют интегралами.

Пример. Корабль водоизмещением 9000 т имеет центр тяжести в точке с координатами х_С = 4,2 м, у_С = 0, z_С = 8,4 м (ось Ох направлена в нос, ось Оу - на левый борт, ось Оz - вверх). С корабля снимают часть груза массой 300 т, координаты центра тяжести которого: х₁= 6м, y₁= 0,8 м, z₁ = 6 м. Определить новые координаты центра тяжести корабля.

Примечание: 3десь и в дальнейшем под водоизмещением корабля понимается масса вытесненной им воды.

Решение. Обозначим m₂ массу корабля после снятия груза; х₂, у₂, z₂ - искомые координаты центра тяжести. Используя формулы (13)

,

находим

м; м; м.

Таким образом, центр тяжести корабля сдвинулся к корме, к пра­вому борту и вверх.

Задачи Центр тяжести линии

2.5.1. Определить координату х_С центра тяжести контура ABD (рис. 338), состоящего из однородных стер­жней АВ, AD и BD, имеющих одинаковый ли­нейный вес, если АВ = 2 м и угол α = 30°. (0,634)

2.5.2. Определить в см координату у_С центра тяжести однородной проволоки (рис. 339), состоящей из прямолинейного отрезка ОА и дуги АВ окруж­ности радиуса r = 20 см. (7,78)

2.5.3. Контур ОАВО состоит из прямолинейных отрезков ОА, ОВ и дуги АВ окружности ра­диуса r = 10 см (рис. 340). Определить в см² статический момент этого контура относительно оси Ох. (150)

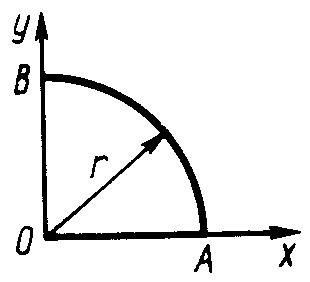
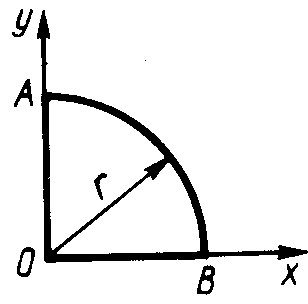
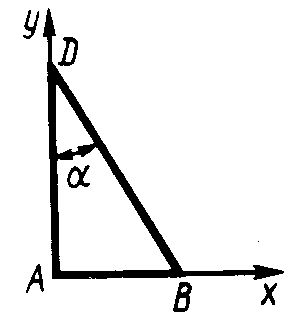
Рис. 338 Рис. 339 Рис. 340

2.5.4. Однородная проволока (рис. 341), согнутая в виде полуокружности, подвешена, как показано на рисунке. Определить угол α между вертикалью и диаметром полуокружности. (32,5)

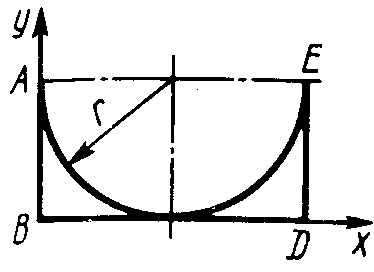
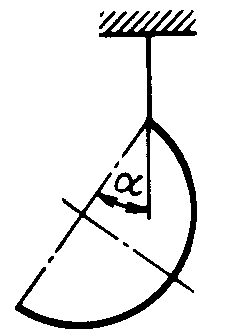
2 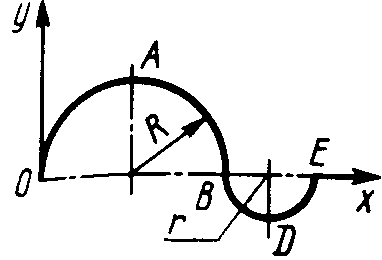.5.5. Контур состоит из двух однородных про­волок, согнутых в виде полуокружностей (рис. 342). Ли­нейный вес проволоки ОАВ равен 6 Н/м, а проволоки BDE - 10 Н/м. Определить коорди­нату х_C центра тяжести контура. (0,673)

Рис. 341 Рис. 342 Рис. 343

2.5.6. Определить координату у_C центра тяжести контура ABDEA (рис. 343), состоящего из прямолиней­ных отрезков АВ, BD, DE и полуокружности радиуса r = 1,2 м. (0,360)

2.5.7. Контур ОАВО состоит из прямолинейного отрезка ОА и полуокружности (рис. 344). Определить радиус r, если координата у_C центра тяжести этого контура равна 0,4 м. (1,03)

2.5.9. Определить координату х_C центра тяжести проволоки ABD (рис. 345), если даны следующие разме­ры: а = 1 м, b = 0,5 м, с = 0,8 м. (0,379)

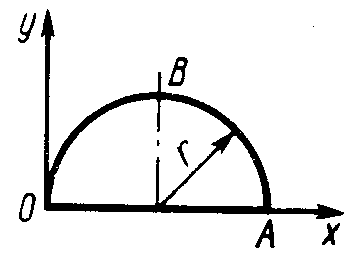
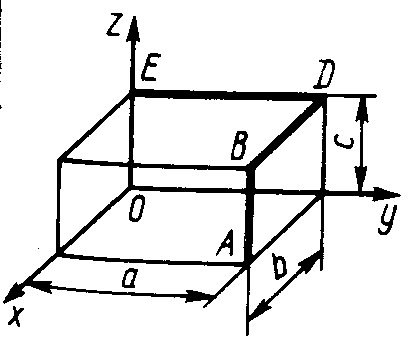
Рис. 344 Рис. 345 Рис. 346

2.5.10. Определить координату у_C центра тяжести проволоки ABDE (рис. 346), если даны следующие раз­меры: а = b = 2м, с = 1м. (1,60)