1.3. Поступательное и вращательное движения

1.3.1. Поступательное движение твердого тела

1.3.1. Сколько независимых уравнений движения описывают поступа­тельное движение тела? (3)

1.3.2. При вращении кривошипа ОА = O₁B = 0,16 м угол φ (рис. 23) изменяется по закону φ = πt. Определить радиус кривизны траектории точки D полукруга ABD при

t = 1 с, если АД = 0,25 м. (0,16)

1.3.3. К ползунам 1 и 2, перемещающимся вдоль оси

Ох по общей направляющей (рис. 24), прикреплено тело 3.

Точка А движется по закону х_А = 0,1 t². При t = 10 с

определить скорость точки С, если расстояния

А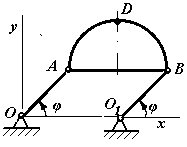 В = ВС = 0,3 м и угол α = 75°. (2)

Рис. 23 Рис.24

1.3.4.В корпусе 1 (рис. 25) по направляющим перемещается пол-зун 2 по закону х_А = 0,1 cos t, у_А= 0, z_A = 0. В момент времени (с) t = π определить скорость точки В, если расстояние АВ= 0,3 м. (0)

Рис. 25 Рис.26

1.3.5. Перо 1 самопишущего прибора (рис.26) перемещается по плоскости S, параллельной плоскости Оху. Приводной шток 2 движется по закону

x_B = 0,1(1 – е^-0,1t), y_B = 0, z_B = 0. В момент времени t = 20 с определить скорость пера (точки А), если x_A = x_B, у_A = 0,2 м и z_A = - 0,1 м. (1,35 ·10^-3)

1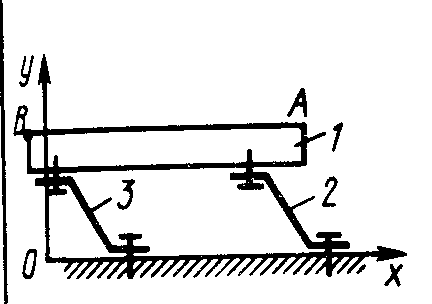 .3.6. Вибролоток 1 (рис. 27), закрепленный на двух плос­ких пружинах 2 и 3, совершает поступательное движение по закону

x_A = 0,16 sin 50 πt,

y_A = 0,12 sin 50 πt,

где x_A и у_A - в см.

Опреде­лить скорость в см/с точки В вибролотка в момент времени t = 1 с,

Рис. 27 если АВ = 100 см. (31,4)

1.3.7. На прямолинейном участке пути центр В спарника тепловоза (рис.28) движется по закону

х_В = 15t - 0,25 cos 30 t, у_B = 0,5 - 0,25 sin 30 t.

В момент времени (с) t = π определить скорость точки С спарника, если ВС = 1,5 м. (16,8)

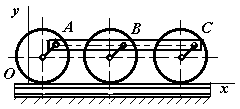
Рис. 28

1.3.8. Тело 3, установленное на двух цилиндри­ческих катках 1 и 2, совершает поступательное движение (рис. 29). Чему равно ускорение точки С, если ускорение точки А равно 2 м/с², причем ВС = 2АВ = 1 м. (2)

1.3.9. Траверса 1 (рис. 30) перемещается по двум вертикальным направляющим 2 и 3 по закону x_A = 0, у_A = 0 и z_A = 1+ 0,1 cos πt. При t = 10,6 с определить ускорение точки В траверсы, если ее координаты х_В = 0,3 м, у_В = 0 6 м, z_B = z_A. (0,305)

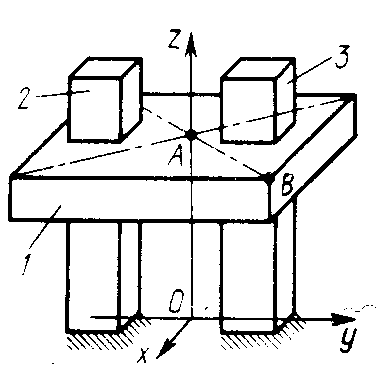
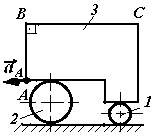
Рис. 29 Рис. 30

1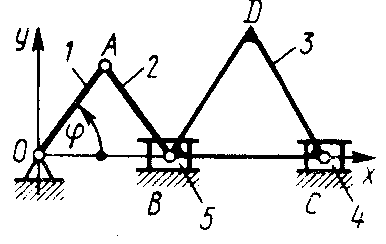 .3.10. При вращении кривошипа 1 шатуном 2 (рис.31) приводятся в движение ползуны 4, 5 и тре­угольная пластинка 3. В

Рис. 31 момент времени t = 0,5 с определить ускорение точки D, если ОА=АВ=0,2 м, ВС = CD = BD = 0,26 м, угол φ= π t. (0)

1.3.12. На двух кривошипах 1 и 2 одинаковой длины ОА = O₁В = 0,2 м закреплен стержень 3, совершающий движение в плоскости Oху (рис. 32). Точка А движется по закону s = 0,2 πt. Опре­делить ускорение средней точки С стержня при t = 0, если АВ = 0,36 м. (1,97)

1.3.13. Круглый стол 1 приводится в поступатель­ное движение с помощью кривошипов 2 и 3 (рис. 33). Определить скорость центра С стола, если из­вестно, что нормальное ускорение точки А кривошипа = 5 м/с², а длина кривошипа ОА = O₁В = 0,2 м. (1)

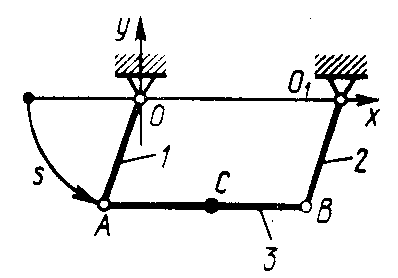
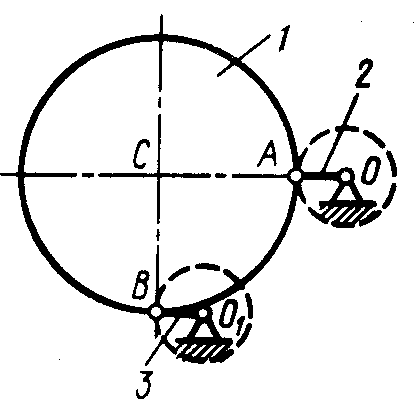
Рис. 32 Рис. 33

1 .3.14. Квадратная пластина ABCD (рис.34) совершает поступательное движение в плоскости Оху. Определить ускорение точки С, если известно, что нормальное ускорение точки = 4 м/с², а касательное ускорение точки = 3м/c². (5)

Рис. 34