1.4. Плоскопараллельное движение твердого тела

1.4.1. Уравнения движения и скорости точек плоской фигуры

Уравнения движения плоской фигуры в неподвижной системе координат:

x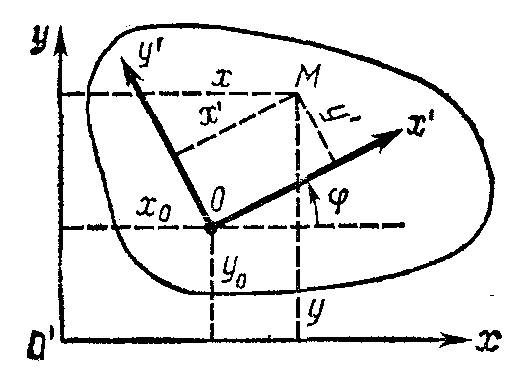 ₀ = x₀(t); y₀ = y₀; φ = φ(t), (39)

где x₀ и y₀ - координаты произвольной точки О, принятой за полюс; φ - угол между неподвижной осью О₁х и осью Ох', неизменно связанной с фигурой (рис. 63). Уравнения движения любой

Рис. 63 точки плоской фигуры имеют вид

x = x₀ + x'cosφ — y'sinφ; (40)

y = y₀ + x'sinφ + y'cosφ,

г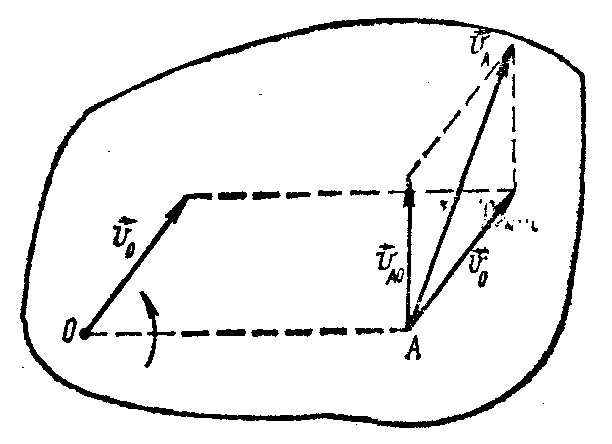 де х', у'—координаты этой точки в системе, скреплен­ной с фигурой.

Скорости двух любых точек плоской фигуры О и А связаны между собой зависи-мостью (рис. 64)

, (41)

где

(42)

Рис. 64 - вращательная скорость точки А относительно О, направленная перпендикулярно отрезку ОА в сторону вращения фигуры и равная по модулю

v_OA = ωOA. (43)

В этих формулах есть мгновенная угловая скорость плоской фигуры.

Если за полюс О принять мгновенный центр скоро­стей Р, т. е. точку, скорость которой в данный момент равна нулю, то скорость любой точки А перпен­дикулярна отрезку РА, направлена в сторону вращения фигуры и равна по модулю

v_A = ω·PA. (44)

Таким образом,

. (45)

Для нахождения мгновенного центра скоростей доста­точно знать направления скоростей двух каких-либо точек плоской фигуры: мгновенный центр скоростей находится на пересечении перпендикуляров, восставленных из дан­ных точек к направлениям их скоростей. Если эти перпендикуляры сливаются в один, то для нахождения мгно­венного центра скоростей надо дополнительно знать модули скоростей.

Мгновенный центр находится в этом случае в точке пересечения общего перпендикуляра и прямой, соединяющей концы скоростей. Если же перпен­дикуляры параллельны, то мгновенного центра не сущест­вует. В этом случае ω = 0, а скорости всех точек плоской фигуры одинаковы по модулю и по направлению.

Если плоская фигура, ограниченная некоторым контуром, катится без скольжения по другому неподвижному контуру, то точка их соприкосно­вения в данный момент является мгновенным центром скоростей этой фигуры.

Теорема: проекции скоростей двух точек плоской фигуры на пря­мую, соединяющую эти точки, рав­ны между собой, т. е.

пр_АВ = пр_АВ (46)

Проекции вектора и на оси, связанные с фигурой, определя­ют по формулам

. (47)

Пример 1. Кривошип ОА механизма (рис. 65) вра­щается с угловой скоростью ω₀. Определить скорости точек В и С, угловую скорость звена BD в том положении механизма, когда α = 30°, β = 60°, а шатун ВС занимает вертикальное положение. Принять ОА= АВ =а; BD = a√3.

Решение. Механизм совершает плоскопараллельное движение. Ведущим звеном, движение которого задано, является кривошип ОА, совершающий вращение вокруг оси О. Определим модуль скорости конца кривошипа, то есть точки А:

ν_А = ω₀ ОА = ω₀ а

Вектор перпендикулярен ОА и направлен в сторону вращения кривошипа. Перейдем к звену АВ. Найдем скорость точки В.

Вектор направлен перпендикулярно BD, так как точка В принадлежит одновременно и звену BD, которое может вращаться вокруг точки D.

Мгновенный центр скоростей звена АВ находится в точке Р пересечения перпендикуляров к и . Из ΔАВР находим ВР = , АР = а/2.

П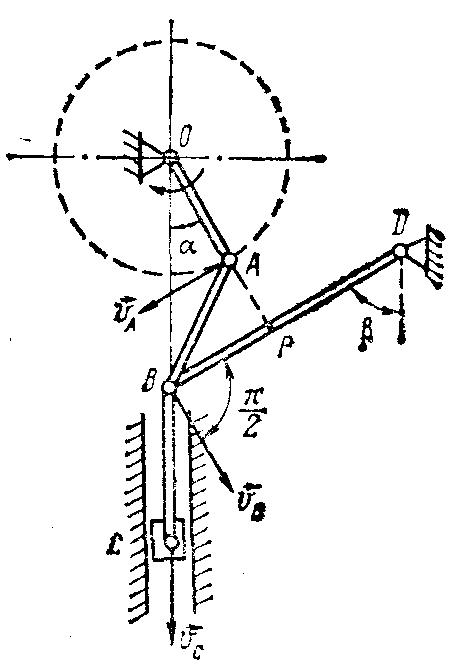 о формуле (44), v_A = ω_AВ ·AP, откуда

ω_АВ = v_А/АР = 2ω_0.

Пользуясь этой же формулой, определим

v_В = ω_AВ ·ВP = ω₀ а√3.

Перейдем к звену ВD. Зная скорость точки В, найдем ω_ВD = v_B /BD = ω₀.

Далее рассмотрим движение звена ВС Используя теорему о проекциях скоростей двух точек, получим

пр_ВС = пр_ВС = v_C .

Отсюда

v_C = v_B cos 30˚ = 3aω₀/2.

Направления скоростей и

Рис. 65 показаны на рисунке 65.

Задачи

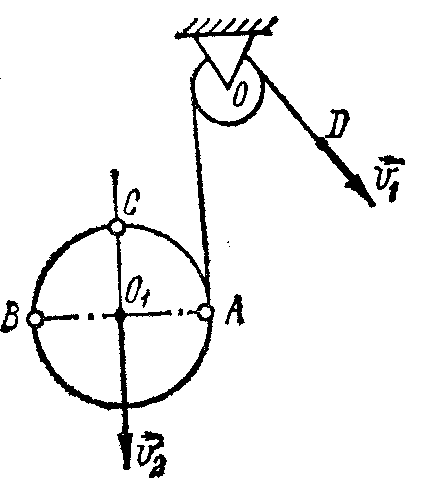
1.4.1.* Цилиндр радиусом R обмотан тросом, перекинутым через блок О (рис. 66). Конец троса тянут со скоростью, в то время как центр цилиндра имеет скорость _. Определить угловую скорость

Рис. 66 цилиндра, счи­тая участок троса от

цилиндра до блока вертикальным. Найти модули скоростей точки В на горизонтальном диаметре

цилиндра и точки С на верти­кальном диаметре.

Ответ: .

1.4.2.* Подъем трубы производится с помощью тале-вого ступенчатого барабана А (рис. 67), вал которого д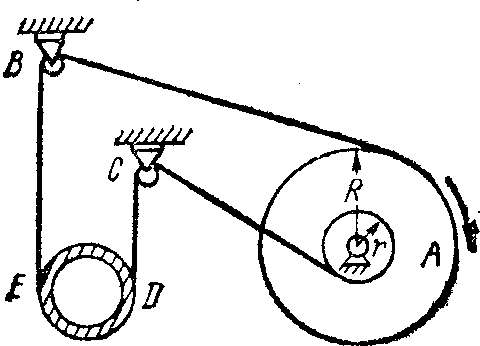 елает 10 об/мин. Определить модуль скорости оси трубы, если r = 5 см, R = 15 см. Участки тросов ВЕ и DC считать вертикальны-

Рис. 67 ми. Ответ: v = 5,24 см/с.

1.4.3.*В механизме (рис. 68) («римская передача») ведущее зубчатое колесо I вращается с угловой ско­ростью ω₀. Определить модуль скорости штока CD в момент, когда α = 90°, если при этом шарниры А₁ и А₂ ле­жат на прямой, проходящей через центры O₁ и О₂ и па­раллельной звену В₁В_2. Радиусы колес соответственно равны r₁ и r₂; О₁А₁ = а₁; О₂А₂ = а₂; СВ₁=СВ₂.

О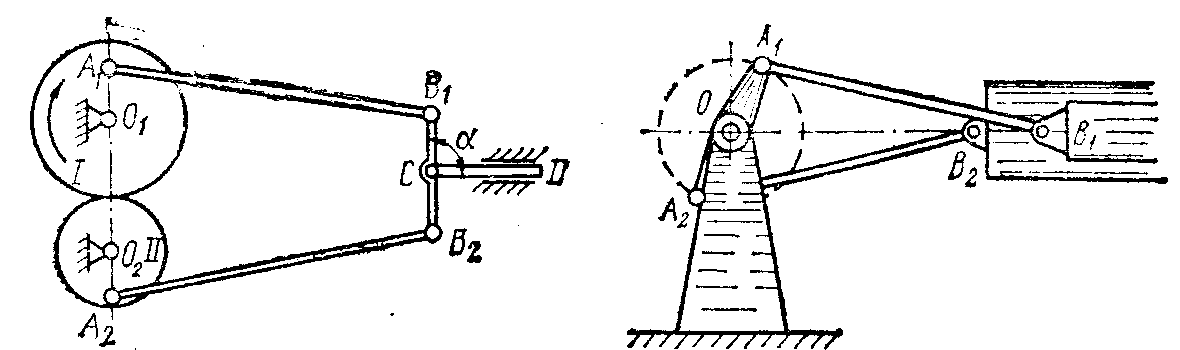 твет: v = ω₀ (a₁r₂ + a₂r₁)/2r₂.

Рис. 68 Рис. 69

1.4.4.* Доказать, что отношение скоростей порш­ней B₁ и B₂ в механизме компрессора (рис. 69) в любой момент времени такое же, как и отношение расстояний от них до центра вращения кривошипа, если OA₁= OA₂, а А₁В₁ = А₂В₂

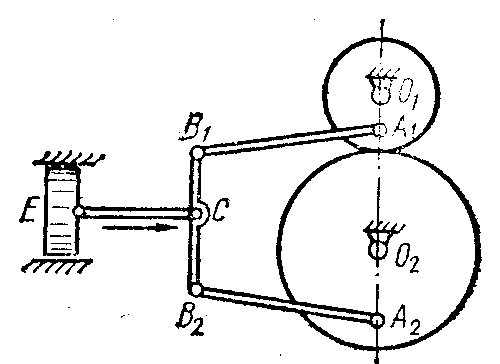
1.4.5.* На рис. 70 изображен механизм газового двигателя. Определить угловые скорости зубчатых колес в момент, когда звено В₁В₂ параллельно линии центров, шток ЕС - горизонтален, а точки крепления тяг А₁ и А₂ занимают наинизшее положение, если в этот момент скорость поршня равна v. Дано: О₁А₁= а₁; О₂; О₂А₂ = а₂; CB₁= b₁; СВ₂= b₂; радиусы r₁ и r₂ (a₁b₂r₂ ≠ a₂b₁r₁)

О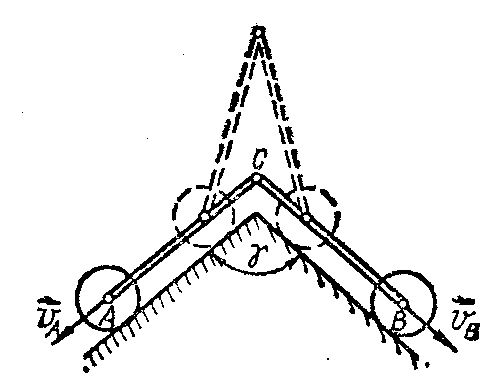 твет: (если знаменатель положителен, то колесо I вращается против дви­жения часовой стрелки).

Рис. 70 Рис. 71

1.4.6.* (рис. 71). Два катка положены на наклон­ные плоскости, образующие между собой угол γ, так, что они могут катиться по этим плоскостям без сколь­жения. Центры катков А и В шарнирно соединены со стержнями АС и ВС, имеющими общий шарнир С. Опре­делить модуль скорости точки С в момент, когда стержни параллельны соответствующим плоскостям, если при этом центры катков имеют скорости и соответственно.

Ответ:

1.4.7. Зависят ли при плоскопараллельном движении значение и направ­ление угла поворота твердого тела от выбора полюса? (Нет)

1.4.8. Зависит ли при плоскопараллельном движении твердого тела вид уравнений движения полюса от его выбора? (Да)

1.4.9. Стержень АВ (рис.72) движется согласно уравнени­ям х_А = 2 + t², y_A = 0, φ = 0,25 π t. Определить абсциссу точки В в момент времени t₁ =1 с, длина АВ=3 м. (0,879)

1.4.10. Центр колеса, катящегося по прямолиней­ному участку пути (рис.73), движется согласно урав­нениям

х_С = 0,3 t², у_C = 0,15 м. Определить в момент времени

t₁ = l c ординату точки В, если в начале движения прямая АВ совпадала с осью Оу. (0,212)

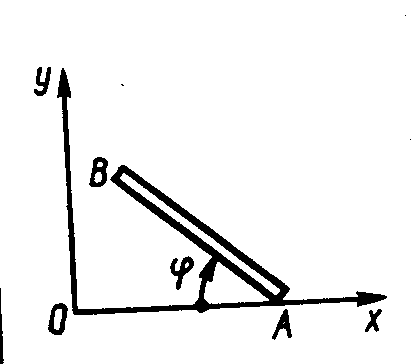
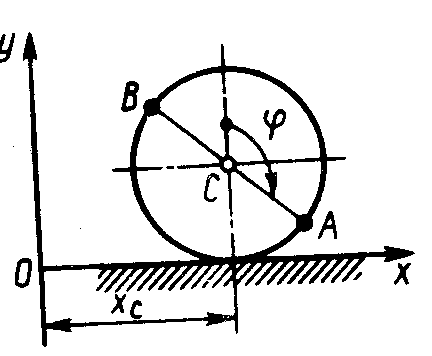
Рис. 72 Рис. 73

1.4.11. Балка AD (рис.74) движется согласно уравнениям х_А = t²_, y_A = 0, φ = arc sin {2/ [4 + (3,5 - t²)²]^0,5}. Определить абсциссу точки А в положении балки, когда ее угол поворота φ = 38°. (0,940)

1.4.12. Вершины А и В треугольника (рис. 75) во время движения все время находятся соответственно на осях Оу и Ох. Определить угол поворота φ в момент вре-мени t₁ = 2 с, если вершина В из положения x_B (0) = 2 м начала перемещаться с постоянной скоростью v _B = 0,5 м/с; длина АВ = 4 м. (0,846)

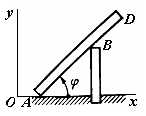
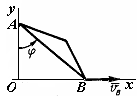
Рис. 74 Рис. 75

1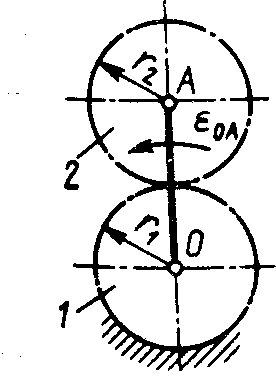 .4.13. Колесо радиуса R = 10 см катится по прямолинейному участку пути с постоянным ускорением центра колеса а_C = 2π cм/с². Определить, сколько оборотов совершило колесо в момент времени t = 10 с, если скорость v_C (0) = 0. (500)

1.4.14. Кривошип ОА (рис. 76) начал равномерно вра­щаться из состояния покоя с угловым ускоре­нием ε_OA = 0,1π. Определить, сколько оборо­тов совершит шестерня 2 по истечении 10 с. Радиусы

шестерен r₁ = r₂ = 10 см. (5)

Рис. 76