1.1.2. Скорость и ускорение точки в декартовых координатах

При задании движения точки в прямоугольных декар­товых координатах скорость и ускорение точки опреде­ляются по их проекциям на неподвижные оси:

; ; ; (3)

; ; ; (4)

; (5)

; (6)

; ; ; (7)

; ; . (8)

Уравнения годографа скорости в параметрическом виде:

; ; , (9)

где х₁, у₁, z₁ - текущие координаты точки, вычерчиваю­щей годограф, а оси О₁х₁, O₁y₁, O₁z₁, соответственно па­раллельны осям Ох, Оу, Оz.

Пример 3. Даны уравнения движения точки; x = t²; y = t³/3. Определить: траекторию точки, скорость точки в момент t = 1 c, годограф скорости, ускорение точки при t = 2 c.

Решение. 1. Исключая t из уравнений движения, получим урав­нение кривой, по которой движется точка:

(полукубическая парабола). Траекторией является часть этой параболы, соответствующая x ≥ 0.

2. Находим проекции скорости точки на оси координат по фор­мулам (3)

; ,

откуда . Следовательно, v |_t=l = √5 = 2,24.

Направление скорости определяется направляющими косинусами (7):

; ;

При t =1 c

; .

Таким образом, скорость в момент t = 1 c составляет с осями Ох и Оу соответственно углы 26°34' и 63°26'.

3. Находим уравнения годографа скорости в параметричес-ком виде по формулам (9): ; .

Исключая t, получим .

Годографом скорости точки является часть этой параболы, соот­ветствующая (0 ≤ x₁< ).

4. Находим проекции ускорения точки на оси координат по фор­мулам (4):

; .

Отсюда , следовательно,

a│_t=2 = 2√5 = 4,47.

Направление ускорения определяется направляющими косинусами по формулам (8):

; .

При t = 2 получим ; .

Таким образом, вектор в момент t = 2 образует с осями Ох и Оу соответственно углы 63°26 и 26°34'.

Пример 4. Груз С поднимается по верти­кальной направляющей с помощью троса, перекинутого через неподвижный блок А (рис. 8)., отстоя­щий от направляющей на расстоянии АО = b. Определить скорость и уско­рение груза С в з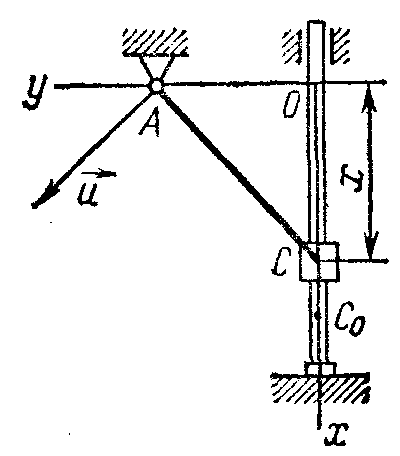 ависимости от расстояния ОС = х, если свободный конец троса тянут с постоянной ско­ростью и.

Решение. Из треугольника АОС .

Пусть С₀ - начальное положение груза. Обозначая АС₀= l, получим AC = l – ut, и уравнение движения груза С примет вид

Рис. 8 .

Находим проекцию скорости на ось Ох:

.

Из уравнения движения груза находим

= ,

следовательно .

Знак минус указывает на то, что точка движется в сторону умень­шения абсциссы х, т. е. вверх.

Находим проекцию ускорения точки на ось Ох:

.

Так как , то окончательно получим

.

Знак минус указывает на то, что ускорение точки направлено также вверх таким образом, движение груза ускоренное.

Задачи

1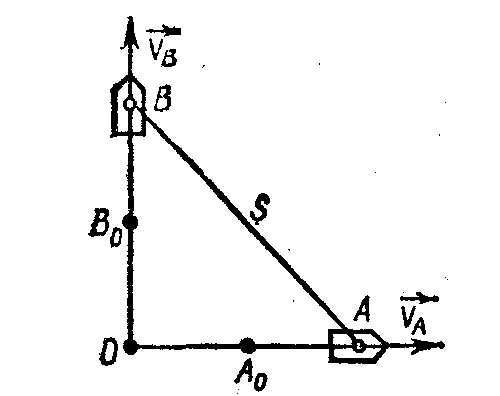 .1.10.* Два судна А и В идут взаимно перпендикулярными курсами (рис. 9) с постоянными скоростями, равными по модулю 20 узлам (узел — единица скорости, равная миле в час). Определить закон изменения расстоя­ния s между ними, если в

Рис. 9 начальный момент суда зани­мали положения А₀ и B₀, причем ОА₀ = ОВ₀ = 3 мили.

Ответ: s = √2 (3 + 20t) миль (t- в часах).

1.1.11. Дано уравнение движения точки . Определить модуль скорости точки в момент времени t = 2 с. (4,47)

1.1.12. Дан график скорости движения точки (рис.10) . Определить пройденный путь в момент времени t = 5 с. (7,5)

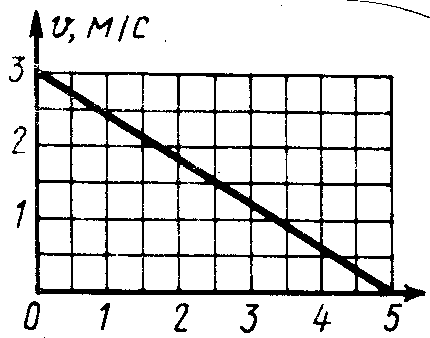
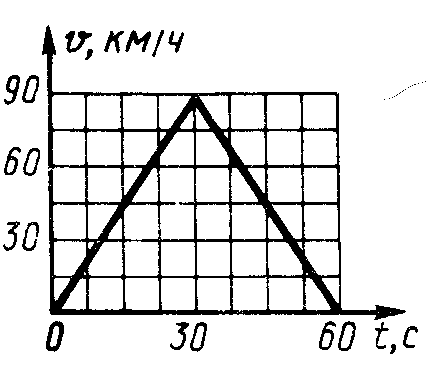
Рис. 10 Рис. 11

1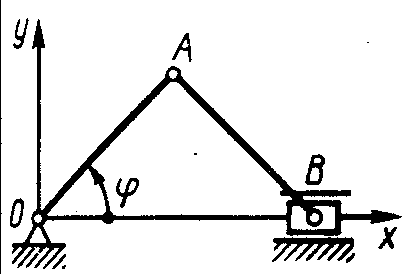 .1.13. Дан график скорости движения точки v = f(t) (рис.11).Определить пройденный путь в мо­мент времени t = 60 с. (750)

1.1.14. Положение кривошипа (рис.12) определяется уг­лом φ = 0,5t.

Рис. 12 Определить скорость ползуна В в момент времени t = 4 с, если ОА = АВ = 1,5 м. (-1,36)

1.1.15. Даны уравнения движения точки х = t², у = sin πt, z = cos πt. Определить модуль скорости точки в момент времени t = 1 с. (3,72)

1.1.16. Скорость движения точки . Определить угол в граду­сах между вектором скорости и осью Ох в момент времени t = 4 с. (20,6)

1.1.17. Проекция скорости точки v_х = 2 cos πt. Определить координату х точки в момент времени t = 1 с, если при t₀ = 0 координата х₀ = 0. (0)

1.1.18. Дано уравнение движения точки х = sin πt. Определить скорость в ближайший после начала движения момент времени t, когда координата х = 0,5 м. (2,72)

1.1.19. Заданы уравнения движения точки . Определить координату х точки в момент времени, когда ее координата у=12 м. (1,78)

1.1.20. Задано уравнение движения точки . Определить координату у точки в момент времени, когда r = 5 м. (4)

1.1.21. Заданы уравнения движения точки . Определить расстояние точки от начала координат в момент времени t=2 c. (7,21)

1.1.22. Скорость автомобиля равномерно увеличивается в течение 12 с от нуля до 60 км/ч. Определить ускорение автомобиля. (1.39)

1.1.23. Сколько секунд должен работать двигатель, который сообщает ракете ускорение 3g, чтобы скорость ракеты в прямолинейном движении возросла с 3 до 5 км/с? (68,0)

1.1.24. Самолет при посадке касается посадочной полосы с горизонтальной скоростью 180 км/ч. После пробега 1000 м самолет останавливается. Определить модуль среднего замедления самолета. (1,25)

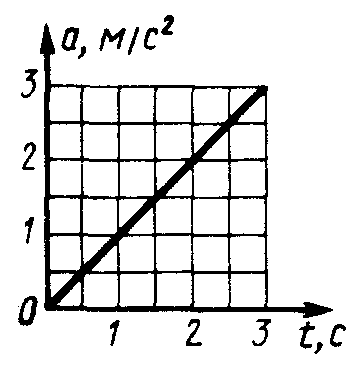1.1.25. Дан график ускоре-ния а = f(t) прямолинейно движущейся точки (рис. 13). Определить ско­рость точки в момент времени t = 2 с, если при t₀ = 0 скорость v₀ = 0. (2)

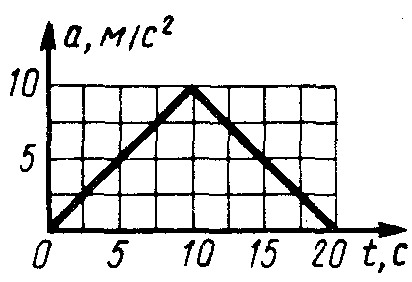Рис.13 1.1.26. Дан график ускорения а = f(t) прямоли­нейно движущейся точки (рис.14). Определить скорость точки в момент времени t = 20 с, если при t₀= 0 скорость v₀= 0. (100)

Рис. 14

1.1.27. Скорость автомобиля 90 км/ч. Определить путь торможения до остановки, если среднее замедление автомобиля равно 3 м/с см, а закон изменения угла φ = 3t. (104)

1.1.28. Ускорение точки . Определить модуль ускорения в момент времени t = 2 с. (1,28)

1.1.29. Скорость точки . Определить модуль ускорения точки в момент времени t = 1,5 с. (3,13)

1.1.30. Определить ускорение точки В (рис.15) в момент времени, когда угол φ = 60°, если длина ОА = АВ = 20 (-1,8)

1.1.31. Определить ускорение точки В (рис. 16) в момент времени t =5 с, если длина кривошипа ОА = 15 см, а закон изменения угла φ = 3t. (-2,19)

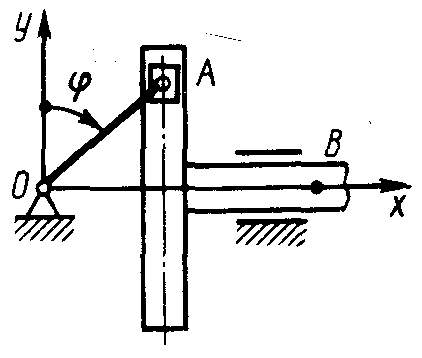
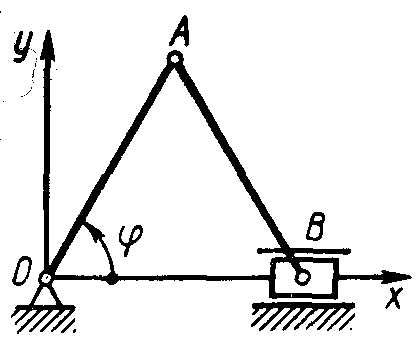
Рис. 15 Рис.16

1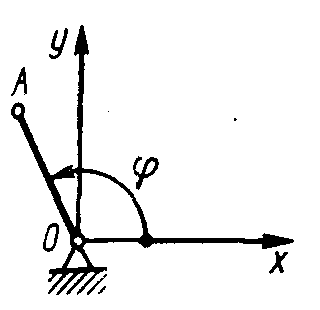 .1.32. Положение кривошипа ОА (рис.17) определяется углом φ = 2t. Определить проекцию ускоре­ния а_х точки А в момент времени t = 1 с, если длина ОА = 1 м. (1,66)