Проектируя это векторное равенство на оси, получим:

х = O₂O₁ sin φ + O₁A sin ψ = (2r + l) sin φ,

у = - O₂О₁ cos φ + O₁A cos ψ = l cos φ.

Отсюда следует, что точка В в процессе движения перемещается вдоль оси О₂х, так как у_В = у_А – l соs φ=0.

Подставляя φ = kt, получим уравнения движения точки А:

х = (2r + l) sin kt, y = l cos kt,

которые одновременно являются и уравнениями траектории точки в параметрической форме. Исключая время t, получим уравнение кривой, по которой движется точка, в непараметрической форме.

Для исключения t перепишем уравнения движения в виде

х/(2r + l) = sin kt; y/l = cos kt.

Пользуясь тождеством sin² kt+cos² kt =1, получим

. (а)

Это эллипс с полуосями а =2r + l, b = l и центром в начале ко­ординат. При изменении t от 0 до ∞ абсцисса х изменяется в преде­лах –a ≤ x ≤ a, а ордината у - в пределах –b ≤ y≤ b, и, следовательно, точка в своем движении обходит весь эллипс. Таким образом, в данной задаче вся кривая, определяемая уравнением (а), является траекторией точки.

Задачи

1.1.1.* По заданным в векторной форме уравне­ниям движения точки определить ее траекторию:

1) = (2t+1) +(2-3t) ;

2) = (2+3t) +(1-2t) +(2+t) ;

3) = t² +(5-2t²) ;

4) = 3 cos + ;

5) = (2+sin ) +(l+2cos ) ;

6) = 6cos2t +t ;

7) = (3 + 2 cos 2t) + (2 -3 sin 2t) ;

8) =3 sin t³+2 cos t³ ;

9) = t +(2t - t²) ;

10) = cos 2t +sin t .

Ответы:

1) Зх + 2у = 7; z = 0 (l ≤ x ≤ );

2) (2≤ х ≤ );

3) 2 х + z = 5; y = 0 (0≤ x ≤ );

4) х² + (y - l)² = 9; z = 0;

5) (х - 2)² + (z -1)²/4 = 1; y = 0;

6) y = 6 cos 2z; x = 0 (0 ≤ z ≤ );

7) ; z = 0;

8) y²/9 + z²/4 = 1; x = 0;

9) y = 2x - x²; z = 0 (0 ≤ x < );

10) x = l - 2z²; y = 0 (-l ≤ x ≤ l).

1.1.2.* По заданным уравнениям движения точки найти ее траекторию в плоскости хОу и начальное поло­жение:

1) x = 2sin ; y = 3cos ;

2) x =3cos t; y =3 -5sin t;

3) x = ; y = e^-t;

4) x = t³ + 2; y = 3 - t³;

5) x = 2 cos 2t; y =3 sin t;

6) x = 4 sin 2t; y =2 cos t;

7) x = 2 tg ; y = 3 sin t (t< π);

8) x = 3 tg ; у = соs t (t < π);

9) x = 3t; y = 6t - 5t²;

10) x = a(sin kt + cos kt); y = b(sin kt – cos kt);

11) x = 2sin t²; y = 3cos t²;

12) x = a + r cos ωt; y= r sin ωt.

Ответы:

1) x²/4 + y²/9 = 1. При t = 0: x₀ = 0; y₀ = 3;

2) . При t = 0: x₀ = 3; y₀ = 3;

3) у = е^-х (0≤ x < ). При t = 0: x₀ = 0; y₀ = 1;

4) x + y = 5 (2≤ x < ). При t = 0: x₀ = 2; y₀ = 3;

5) y² = (- 2≤ x ≤2). При t = 0: x₀ = 2; y₀ = 1;

6) x² = 4y²(4 - y²) (- 4 ≤ x≤ 4 ). При t = 0: x₀ = 0; y₀ = 2;

7) y = (0 ≤ x< ). При t = 0: x₀ = 0; y₀ = 0;

8) y = (0 ≤ x< ). При t = 0: x₀ = 0; y₀ = 1;

9) y = 2x- x² (0 ≤ x< ). При t = 0: x₀ = 0; y₀ = 0;

10) . При t = 0: x₀ = a; y₀ = - b;

11) . При t = 0: x₀ = 0; y₀ = 3;

12) (х - а)² + y² = r². При t = 0: x₀ = a + r; y₀ = 0.

1.1.3.* Точка движется по окружности радиусa r против хода часовой стрелки так, что проходимая ею дуга изменяется по закону s = kt. Найти уравнения движения точки по отношению к системе хОу с началом в центре окружности, если горизонтальная ось Ох проходит через начальное положение точки.

Ответ: x = r cos ; у = r sin .

1.1.4.* Кулиса ОМ длиной l приво­дится в движение кривошипом ОА (рис. 3), вращающимся по за­кону φ = kt². Составить уравнения движения конца ку­лисы М, если O₁O = O₁A.

Ответ: x= l sin ; у = l cos .

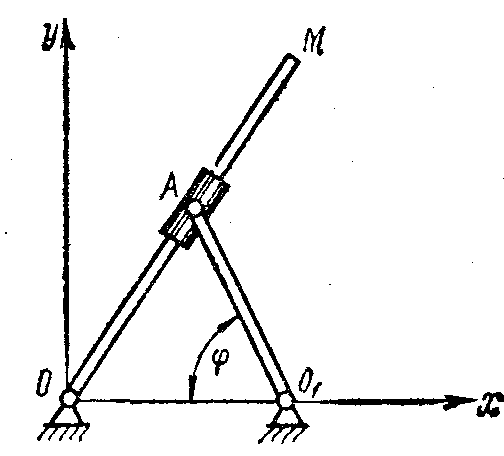
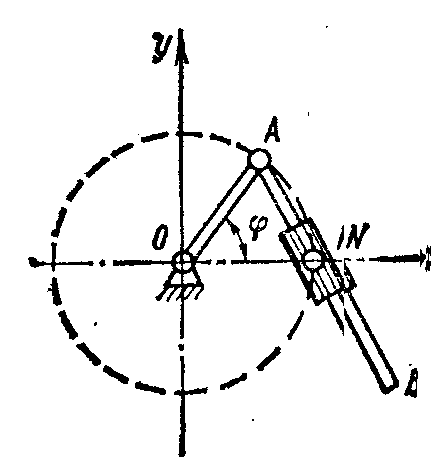
Рис.3 Рис. 4

1.1.5.* Стержень АВ длиной l дви­жется так (рис. 4), что одна из его точек описывает окружность радиусом r = l/2, а сам стержень проходит через неподвижную точку N, лежащую на той же окружности. Составить уравнения движения точки В, если φ = ωt.

Ответ: х = r cos ωt + l sin ; у = r sin ωt – l cos .

1.1.6.* В V-образном двигателе угол между осями цилиндр α =90° (рис. 5). Коленчатый вал вращается по закону φ = ωt. Составить уравнения движения пальцев В и С, если длина кривошипа. ОА = R, а длины шатунов АВ и АС равны L.

Ответ: ;

.

1.1.7.* В V-образном двигателе (рис.5) угол а между осями цилиндров равен 60°. Коленчатый вал вращается по закону φ = ωt. Составить уравнения движения пальцев В и С по направляющим, если длина кривошипа ОА равна R. А длины шатунов АВ и АС равны 2R. Определить положение пальца поршня В в тот момент, когда поршень С находится в крайнем верхнем положении.

Ответ: ;

;

.

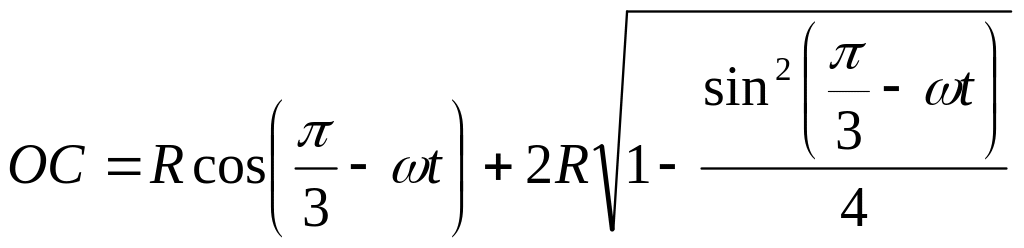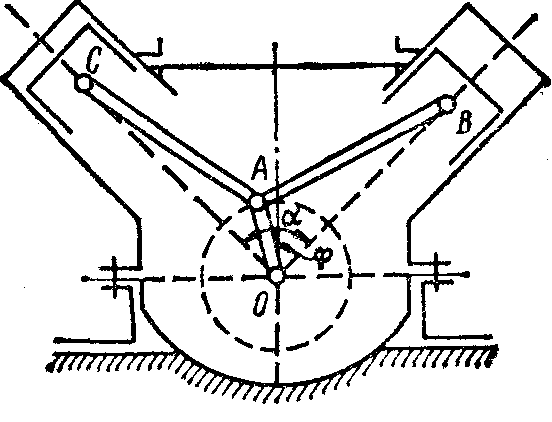
Рис.5 Рис. 6

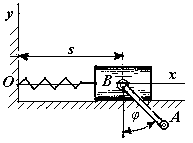
1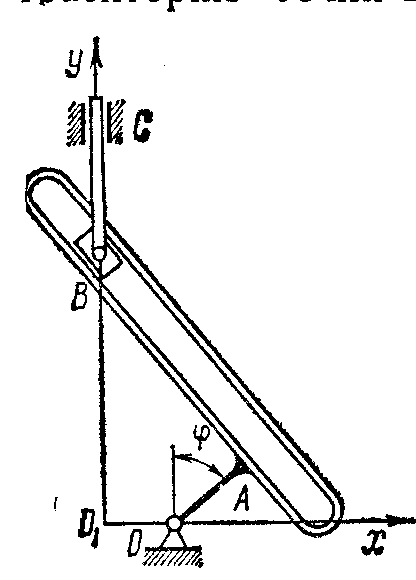 .1.8.* Стержень АВ длиной l поворачивается около точки В (рис.6) так, что угол φ изменяется по закону φ = ωt, а ползун В совершает гармонические колебания согласно уравнению s = a + b sin ωt. Определить траекторию точки А.

Ответ: (х - а)²/(b + l)²+(у²/ l²) =1 (эллипс).

1.1.9.* В механизме (рис. 7) найти уравнение движения точки В, если кулиса ОАВ вращается так, что угол φ = ωt, а расстояние от точки О до направляющей стержня ОО₁ = b,

длина ОА равна а. Угол OAВ – прямой.

Рис.7 Ответ: у = + b tg ωt.