1.4.2. Угловая скорость плоской фигуры

1.4.15. Зависит ли угловая скорость твердого тела при плоскопараллельном движении от выбора полюса? (Нет)

1.4.16. Твердое тело совершает плоскопараллельное движение согласно уравнениям х_А = 2t², у_A = 0,2 м, φ = 10 t². Определить угловую ско­рость тела в момент времени t₁ = 1 с. (20)

1.4.17. В данный момент времени тело совершает мгновенное вращение относительно точки ка­сания его с плоскостью (рис. 77). Определить угловую скорость тела, если скорость точки С равна 10 м/с, а расстояние АС = 20 см. (50)

1.4.18. Определить угловую скорость колеса (рис. 78), если точка А имеет скорость v_A = 10 м/с, а радиус колеса r = 0,2 м. (33,3)

1.4.19. Определить угловую скорость колеса (рис. 79), если точка А имеет скорость v_A = 2 м/с, а радиус колеса r = 1 м. (1,79)

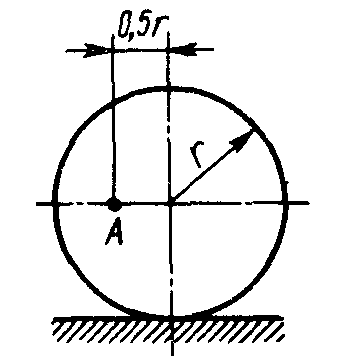
Рис.77 Рис. 78 Рис. 79

1 .4.20. Скорость груза 1 v = 0,5 м/с (рис. 80). Определить угловую скорость подвижного блока 2, если его радиус R = 0,1 м. (2,5)

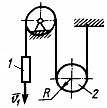
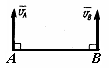
Рис. 80 Рис. 81 Рис. 82

11.4.21. Стержень АВ длиной 60 см движется в плоскости чертежа (рис. 81). В некоторый момент вре­мени точки А и В стержня имеют скорости v_B = v_A = 0,5 м/с. Определить модуль мгновенной угловой скорости стержня. (0)

1.4.22. Стержень АВ длиной 80 см движется в плоскости чертежа (рис. 82). В некоторый момент вре­мени точки А и В стержня имеют скорости v_A = 0,2 м/с, v_B = 0,6 м/с. Определить угло­вую скорость стержня. (0,5)

1.4.23. Барабан лебедки 1 (рис. 83) вращается с угловой скоростью ω = 6 рад/с. Определить угловую скорость поднимаемой трубы 2, если отноше­ние радиусов r/R = 2/3. (1, 5)

1.4.24. Блоки 1 и 2 вращаются вокруг неподвиж­ных осей O₁ и O₂ с угловыми скоростями ω₁= 4 рад/с и ω₂ = 8 рад/с (рис. 84). Определить угло­вую скорость подвижного

блока 3. Радиусы блоков одинаковы и равны r = 10 см. (2)

Рис. 83 Рис. 84

1 .4.25. В дифференциальном механизме (рис. 85) с внутренним зацеплением зубчатое колесо 1 и кривошип ОА вращаются независимо друг от друга с угловыми скоростями ω₁ = 2 рад/с и ω_ОА = 4 рад/с. Определить

Рис. 85 Рис. 86

угловую скорость зубчатого колеса 2, если радиус r₁ = 30 см и длина кривошипа ОА равна 20 см. (2)

1.4.26. Кривошип ОА вращается по закону φ = 0,5 t (рис. 86). Определить угловую скорость колеса 1 планетарного механизма, если длина звена ОА = 0,2 м и радиусы всех колес одинаковы. (0)

1.4.3. Угловое ускорение плоской фигуры

1.4.27. Зависит ли при плоскопараллельном движении угловое ускорение твердого тела от выбора полюса? (Нет)

1.4.28. Тело совершает плоскопараллельное движение согласно уравне­ниям x_A= 2sin 4t, y_A = 2 cos 4 t, φ = 4 t ². Определить угловое ускоре­ние тела. (8)

1 .4.29. Колесо катится согласно уравнениям х_C = 2t², у_C = 0,5 м (рис. 87). Определить угловое ускоре­ние ε колеса. (8)

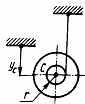
Рис. 87 Рис. 88 Рис. 89

1.4.30. Центр С барабана, разматывающего нить, движется вертикально вниз по закону у_C = 0,33t² (рис. 88). Определить угловое ускорение барабана, если радиус r = 0,066 м. (10)

1.4.31. Барабан 1 (рис. 89) вращается согласно закону φ = 0,3t². Определить угловое ускорение блока 2, если радиусы R = 0,1 м , r = 0,06 м. (0,5)

1.4.32. Кривошип ОА (рис. 90) вращается согласно за-ко­ну φ = 0,5t². Определить угловое ускорение колеса 2. (2)

1.4.33. Кривошип ОА (рис. 91) вращается согласно закону φ = 0,4t². Определить угловое ускорение под­вижной шестерни, если радиус R = 2r = 0,2 м. (0,8)

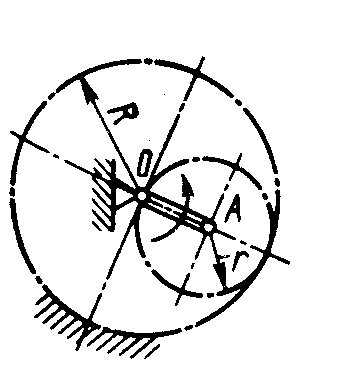
Рис. 90 Рис. 91 Рис. 92

1.4.34. Барабан 1 (рис. 92) вращается согласно закону φ = 0,5t², а ступенчатое колесо 2 катится по наклонной плоскости. Определить угловое ускорение колеса 2, если радиусы r = 0,1 м, R = 0,3м. (0,25)

1.4.35. Для заданного положения механизма (рис. 93) определить мгновенную угловую скорость шатуна АВ, если точка В имеет скорость v_B = 0,4 м/с длина шатуна

B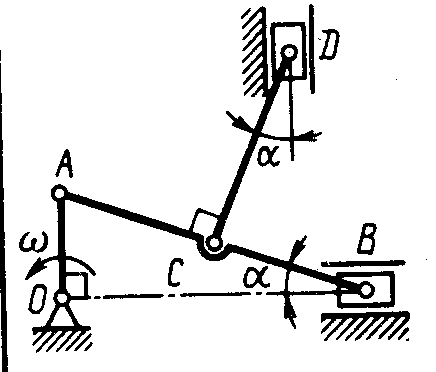 D = 0,5 м, а вектор скорости точки D на ось Ох имеет проекцию v_Dx= 0.2 м/с. (2,4)

Рис. 93 Рис. 94

1.4.36. Кривошип ОА длиной 0,2 м вращается равномерно с угловой скоростью ω = 8 рад/с (рис. 94). К шатуну АВ в точке С шарнирно прикреплен шатун CD. Для заданного положения механиз­ма определить скорость точки D ползуна, если угол α = 20°. (0,582)

63