1.3.4. Преобразование поступательного и вращательного движения тела в механизмах

1.3.49. При движении клина по горизонтальным направляющим со ско­ростью 1 м/с другой клин перемещается в вертикальном направлении со скоростью 1 м/с. Определить угол в градусах скоса клиньев. (45)

1.3.50. Клинья 1 и 3 перемещаются по параллель­ным горизонтальным направляющим, а проме­жуточный клин 2 - по вертикальным направ­ляющим (рис.50). Определить перемещение клина 3, если перемещение клина 1 равно 0,12 м, а угл α = 30° и β = 60°. (0,04)

1 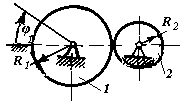.3.51. Колесо 1 (рис. 51) вращается согласно закону φ₁=20t. Определить число оборотов, совершен­ных коле-сом 2 за время t = 3,14 с, если ради­усы колес R₁ = 0,8 м, R₂ = 0,5 м. (16)

Рис. 50 Рис. 51

1 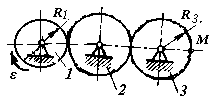.3.52. Зубчатое колесо 1 (рис. 52) вращается равнопере­менно с угловым ускорением ε₁ = 4 рад/с². Определить скорость точки М в момент вре­мени t = 2 с, если радиусы зубчатых колеc R₁ = 0,4 м, R₃ = 0,5 м. Движение начинается из состояния покоя. (3,2)

Рис. 52 Рис.53

1.3.53. Зубчатое колесо 1 (рис. 53) вращается согласно закону φ₁ = 4 t² . Определить скорость точки М колеса 3 в момент времени t =2 с, если радиусы колес R₁= 0,4 м, R₂= 0,8 м, r₂ = 0,4 м, R₃ = 1 м. (3,2)

1.3.54. Редуктор (рис. 54) состоит из конической и цилинд­рической зубчатых передач с числом зубьев колес z₁ = 18, z₂ = 26, z₃ = 28 и z₄ = 40. Вал 1 вращается с угловой скоростью ω = 20 (t + e^-t). В момент времени t = 10 с опре­делить угловую скорость вала 2. (96,9)

Рис.54 Рис. 55

1.3.55. Зубчатое колесо 1 (рис. 55) вращается согласно закону φ₁= 4t². Определить ускорение рейки 3, если радиусы зубчатых колес R₁ = 0,8 м, R₂= 0,4 м. (6,4)

1 .3.56. Вариатор (рис. 56) состоит из ведущего диска 1, ролика 2 и ведомого диска 3. Угловые скорости дисков ω₁= 10 рад/с, ω₂ = 5 рад/с. Опреде­лить отношение расстояний b/d. (2)

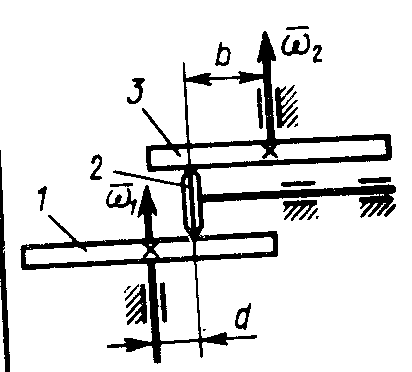
Рис. 56 Рис. 57

1.3.57. Груз 1 поднимается с помощью лебедки 2 (рис. 57). Закон движения груза имеет вид: s = 7 + 5 t², где s - в см. Определить угловую скорость барабана в момент времени t = 3 с, если его диаметр d = 50 см. (1,2)

1.3.58. Какой должна быть частота вращения (об/мин) п₁ шестерни 3 (рис. 58), чтобы тело 1 двига­лось с постоянной скоростью v = 90 см/с, если числа зубьев шестерен z₃ = 26, z₂ = 78 и ра­диус барабана r = 10 см? (258)

Рис.58 Рис. 59

1.3.59. Угловая скорость зубчатого колеса 1 (рис. 59) из­меняется по закону ω₁ = 2t². Определить ус­корение груза 3 в момент времени t = 2 с, если радиусы шестерен R₁ = 1 м, R₂ = 0,8 м и радиус барабана r = 0,4 м. (4)

1.3.60. Зубчатое колесо 3 (рис. 60) вращается равнопере­менно с угловым ускорением ε₃ = 8 рад/с². Определить путь, пройденный грузом 1 за про­межуток времени t =3 с, если радиусы R₂=0,8 м, R₃=0,6 м, r =0,4 м. Груз 1 в начале движения находился в покое. (10, 8)

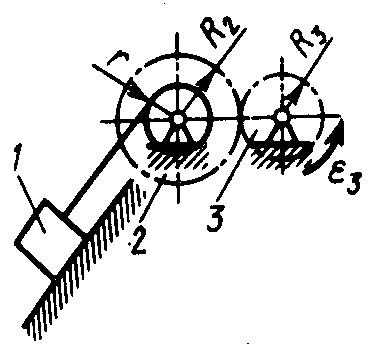
Рис. 60 Рис. 61

1.3.61. Зубчатое колесо 1 (рис. 61) вращается согласно закону φ = 2t³. Определить скорость точки В в момент времени t = 2 с, если радиусы ко­лес R₁ = 0,3 м, R₂ = 0,9 м, длина кривошипа O₁B =ОА = 0,6 м, расстояние 00₁ = АВ. (4,8)

1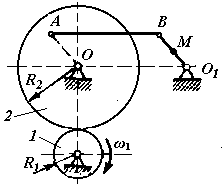 .3.62. Зубчатое колесо 1 (рис. 62) вращается равномер-но с угловой скоростью ω₁ = 6 рад/с. Определить ускорение точки М, если радиусы колес R₁ = 0,3 м, R₂ = 0,9 м, расстояние О₁М = 0,3 м. ОА = O₁B и AB = OO₁. (1,2)

Рис.62